Понятие о фазовом пространстве.

В задачах механики исследование динамики механических систем в т.н. фазовом пространстве. Такое пространство строится на основе полного набора динамических переменных (параметров), где время в явном виде отсутствует. Например, динамическими параметрами в уравнении маятника являются угловая скорость w = dj/dt и угол j. Как известно, первый интеграл уравнения линейного маятника, выражающий закон сохранения энергии, имеет вид

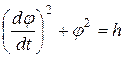, (1.1)

или, в эквивалентной форме 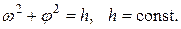Переменные w и j образуют двумерное фазовое пространство, на плоскости первый интеграл изображается окружностями с различными радиусами величиной h^1/2 и определяемые энергией маятника.

Следующим важным понятием является т.н. изображающая точка, такую точку удобно рассмотреть на примере фазового пространства линейного маятника или прикрепленной к пружине массы. Для них уравнения имеют одинаковый вид:

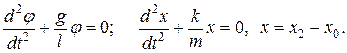
Не привязываясь к конкретной механической системе с конкретной собственной частотой w₀, будем рассматривать просто абстрактную переменную x, ее можно считать и углом и смещением массы на пружине:

.

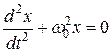Представим изменение x и ее скорости x¢ в следующем виде:

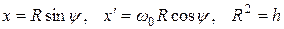. (1.2)

Ясно, что параметры R и y не являются физически реальными радиусом и углом, они существуют только лишь в воображаемом фазовом пространстве. Очевидно, с этими новыми представлениями x и x¢ уравнение (1.1) удовлетворяется автоматически. Новые параметры R и y считаем координатами изображающей точки M в фазовом пространстве маятника. Найдем вторую производную 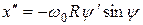и подставим его и x в уравнение маятника. Тогда получим уравнение y ¢ = w₀, или, y = w₀t + y₀, y₀ - начальное значение y. Это означает равномерное движение по часовой стрелке изображающей точки M по окружности фазового пространства (рис. 1.1а).

Таким образом, вся динамика маятника свелась к очень простому результату y = w₀t + y₀ для изображающей точки. Но этот простой результат удалось получить благодаря преобразованиям (1.2), в общем случае подобные удачные преобразования переменных найти в аналитической форме очень трудно, поэтому для этого в современных исследованиях широко применяются компьютеры.

Приведенная на рис. 1.1а фазовая кривая называется центром. Различным энергиям маятника будут соответствовать окружности различного диаметра и на тогда рис. 1.1а получили бы концентрические окружности.

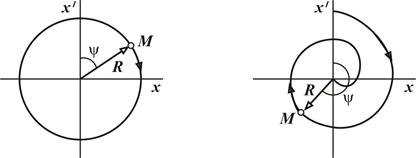
а b

Рис. 1.1. Построение фазового пространства математического маятника (а) и физического маятника (б).

Рассмотрим теперь физический маятник, в нем присутствует сила трения и его уравнение движения имеет вид

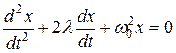. (1.3)

Попытаемся использовать преобразования (1.2), где считаем R зависящей от времени. Вторая производная от x теперь дается выражением

.

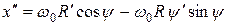Подставим это и x, x¢ из (1.2) в уравнение (1.3), получим

,

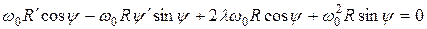или,

.

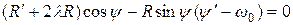Это равенство выполнится при произвольном угле y, только если выражения в скобках будут равны нулю, т.е.

.

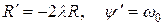Отсюда находим

.

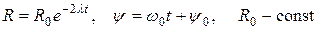Исключив отсюда переменную t и положив для упрощения y₀ = 0, определяем уравнение движения изображающей точки:

.

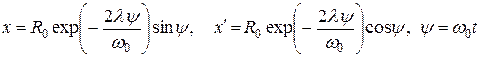Это уравнения спирали, закручивающейся к точке R = 0 (рис. 1.1b), т.е. точка x = x¢ = 0 на фазовой плоскости отвечает устойчивому состоянию. При l < 0 спираль будет раскручиваться, и изображающая точка будет уходить в бесконечность, означающее неустойчивость состояния в точке x = x¢ = 0. Фазовая траектория на рис 1.1b называется устойчивым фокусом, отрицательное значение l < 0 приводит к неустойчивому фокусу.

Наиболее общая дифференциальная форма механической системы с двумя динамическими параметрами X₁, X₂ представляется уравнениями

, ,

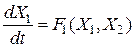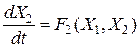где F₁(X₁, X₂) и F₁(X₁, X₂) - заданные функции. С тремя видами фазовых центр, устойчивый фокус и неустойчивый фокус траектории в такой системе мы уже ознакомились выше при анализе гармонических и затухающих колебаний. Другие возможные на плоскости фазовые траектории, по которым проходит изображающая точка, приведены на рис. 1.2. Их отличительной особенностью является уход траекторий в бесконечность или приход из бесконечности.

а b с

Рис. 1.2. Траектории в двумерном фазовом пространстве механической системе с одной степенью свободы: a – устойчивый узел; b – неустойчивый узел; c – седло.

С ростом сложности системы, определяемой числом степеней свободы, фазовое пространство усложняется. В первую очередь растет размерность фазового пространства, для механической системы с тремя степенями свободы фазовую траекторию в трехмерном пространстве еще можно представить на рисунке. Но когда размерность фазового пространства становится большой, то фазовые траектории, как и само пространство можно «видеть» только математическими уравнениями.

В дальнейшем для нас особый интерес представляют системы с фазовыми траекториями, остающимися во все время эволюции в ограниченной области фазового пространства, как в примере с маятником.

2. Элементы механики Гамильтона. Хаотическая динамика в консервативных системах.

Кроме механики Ньютона и Лагранжа есть еще один подход к изучению движения механических систем, это механика Гамильтона. Она очень удобна при рассмотрении систем, состоящих из очень большого числа одинаковых частиц с одинаковыми законами движения для каждой из них. Ярким примером таких систем являются газы, жидкости и твердые фазы одного вещества. Расширение элементов механики Гамильтона на микрочастицы приводит к фундаментальному понятию оператора Гамильтона, или, оператора энергии.

Для получения уравнений движения в механике Гамильтона составляется выражение для полной энергии механической системы:

H = T + U, (2.1)

где T и U - соответственно полная кинетическая и потенциальная энергия. Как видно, функция Гамильтона отличается от функции Лагранжа знаком перед потенциальной энергией.

Пусть механическая система имеет n степеней свободы, каждая степень свободы характеризуется обобщенной координатой q_i и обобщенным импульсом p_i. Это означает, что функция H зависит от 2n переменных: H(q_i, p_i). Тогда уравнения движения Гамильтона имеют вид

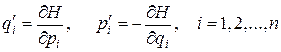. (2.2)

Штрих над буквами означает дифференцирование по времени. Для полного определения эволюции механической системы задаются начальные условия

.

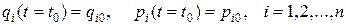При заданных начальных условиях по уравнениям (2.2) можно определить координаты q_i и p_i импульсы в любой последующий момент времени. Тогда эволюцию механической системы можно представить как движение изображающей точки в гиперпространстве размерностью 2n, где осями координат являются переменные q_i и p_i. Рассмотрим в качестве примера гармонический осциллятор, для него полная кинетическая и потенциальная энергия даются выражениями

.

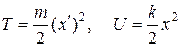Переходя к общим обозначениям, напишем mx¢ = p, x¢ = q¢ (i = 1), или,

.

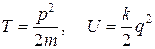Функция Гамильтона

.

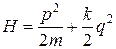Используя уравнения (2.2), получим

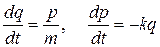. (2.3)

Легко видеть, что это те же самые уравнения, которые мы уже получали ранее. Действительно, продифференцируем первое уравнение по времени:

.

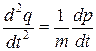Из второго уравнения в (2.3) сюда подставим выражение для производной dp/dt, получим

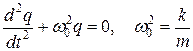. (2.4)

Согласно первому уравнению в (2.3) задание начального условия для импульса p с точность до несущественной константы эквивалентно заданию начального условия для производной dq/dt, поэтому начальные условия для уравнения (2.4) записываются как

.

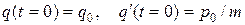Полная энергия гармонического осциллятора E сохраняется, в любое время она остается постоянной величиной: H(q, p) = E = const. Это означает, что движение изображающей точки в фазовом пространстве происходит по линии H(q, p) = E. Это общий вывод для всех систем с сохраняющейся полной энергией. В случае гармонического осциллятора изображающая точка движется по фазовой траектории, называемой кругом или эллипсом (рис. 1.1а):

.

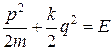При этом неважно, круг или эллипс, поскольку важна их топологическая эквивалентность. Уравнения движения изображающей точки получаются переходом к переменным

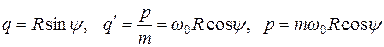, (2.5)

.

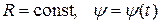После подстановки в (2.4) и решения элементарного дифференциального уравнения для угла y, находим

y = w₀t + y₀. (2.6)

В сущности, этот результат был получен выше, и здесь только идет повторение для последовательности изложения темы. Используя q и p из (2.5) в определении функции H, находим для нее явное выражение:

.

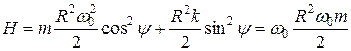Приведем его в компактную и удобную форму:

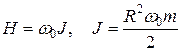, (2.7)

где новый параметр J называется действием.

Как видим, динамика гармонического осциллятора представлена в виде равномерного движения изображающей точки в фазовом пространстве по замкнутой линии и на этой линии энергия постоянна.

На постоянство полной энергии механической системы здесь обращается особое внимание. Для физического маятника полная энергия не сохраняется, там происходит диссипация энергии, которая определена функцией Релея

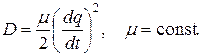
На сохранение энергии внимание уделяется и в рассматриваемых ниже механических системах. Дело в том, что в системах, состоящих из атомов и молекул и находящихся в теплоизолированном сосуде, сложная динамика в виде молекулярного хаоса наблюдается в условиях постоянства полной энергии. У систем с постоянной полной энергией фазовое пространство финитно, т.е. весь спектр возможных значений координат q и импульсов p располагается в ограниченном пространстве.

2.1. Система из двух независимых гармонических осцилляторов. Эргодичность.

Рассмотрим теперь систему из двух гармонических осцилляторов, каждая из них характеризуется своими обобщенными переменными (q₁, p₁) и (q₁, p₁), для них функция Гамильтона следующая:

.

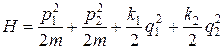Здесь в целях упрощения записи массы полагаются одинаковыми, что несущественно. Для системы из двух осцилляторов фазовое пространство является четырехмерным, уравнения Гамильтона запишутся в виде

.

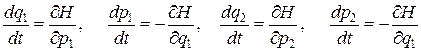После вычисления производных получаются

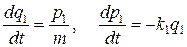, (2.8)

.

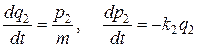Используя предыдущие результаты, а именно - формулы (2.5)-(2.7), можно относительно переменных фазовой траектории выписать решения этих уравнений:

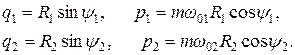(2.9)

Здесь каждый осциллятор имеет свою частоту, они равны

.

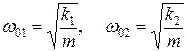Углы y₁ и y₂ меняются со временем по законам

y₁ = w₀₁t + y₀₁, y₂ = w₀₂t + y₀₂.

Функция Гамильтона принимает вид

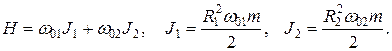
Далее для упрощения и наглядности сделаем формальное переопределение импульсов:

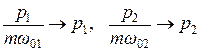. (2.10)

Это позволяет эллипсы фазовых траекторий превратить в окружности и вместо (2.9) имеем

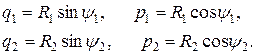
Поскольку угол всегда определяется по модулю 2p, эволюцию системы удобно представить на поверхности тора. Условимся, что переменные R₁ и R₂ обозначают соответственно внутренний радиус и радиус поперечного сечения тора, а угловые переменные y₁ и y₂ меняются в соответствии с поворотом радиусов R₁ и R₂ (рис. 2.1). Тогда при фиксированных радиусах R₁ и R₂ меняющиеся углы y₁ и y₂ определяют изображающую точку, движущуюся по поверхности тора. Если параметрическим образом менять R₁ и R₂, то получатся вложенные друг в друга слои торов.

В приведенном примере частоты w₀₁ и w₀₂ не зависимы, поэтому они являются функциями своих радиусов: w₀₁(R₁), w₀₂(R₂). Но если между осцилляторами появится малейшая связь, то частоты можно представить в виде зависимостей w₀₁(R₁, R₂), w₀₂(R₂, R₂). В общем случае такая связь нелинейная, ее траектория не будет описываться гармоническими функциями, как у линейных осцилляторов. Если для таких сложных систем существует преобразование переменных (q, p) ® (y, J), то они называются полностью интегрируемыми.

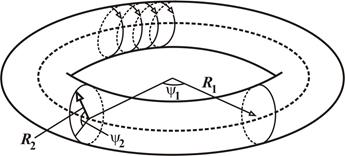
Рис. 2.1. Фазовый портрет динамики двух независимых гармонических осцилляторов.

Поскольку любые замкнутые кривые можно деформациями преобразовать в окружности, то аналогичная картина будет иметь место для любой интегрируемой системы с двумя степенями свободы, т.е. ее фазовые траекторий будут располагаться на концентрических двумерных торах (рис. 2.2).

При этом для нелинейных систем частоты обращения могут меняться при переходе от одного тора к другому тору в силу наличия зависимостей w₀₁(R₁, R₂) и w₀₂(R₂, R₂). Поведение фазовых траекторий существенным образом зависит от того, является ли отношение w₀₁/w₀₂ рациональным или иррациональным числом. Если оно рационально, т.е. w₀₁/w₀₂ = n₁/n₂, где n₁ и n₂ - целые числа, то по истечении интервала времени

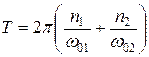
изображающая точка возвратится в исходное место, откуда она начала движение.

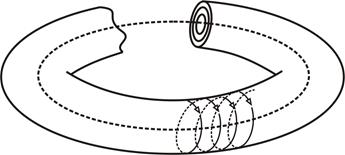
Рис. 2.2. Представление произвольной периодической динамики с различными энергиями как движение по поверхностям тора в фазовом пространстве.

Движение механической системы, очевидно, является периодическим с периодом T. Тор, на котором движение периодическое, называется резонансным. Если же отношение частот w₀₁/w₀₂ является иррациональным числом, то фазовая траектория никогда не замкнется сама на себя, и с течением времени будет подходить сколь угодно близко к любой заданной точке на поверхности тора. Такое движение называется условно периодическим или квазипериодическим, его траектории будут всюду плотно покрывать поверхность тора. Такой тор называется нерезонансным.

Пусть теперь имеется полностью интегрируемая система уравнений с n степенями свободы (2.2). Для такой системы фазовое пространство имеет размерность 2n, и в переменных y, R оно имеет структуру множества n-мерных торов, любая возможная траектория располагается на одном из них. При этом некоторые траектории могут оказаться замкнутыми, другие же будут плотно покрывать поверхность соответствующего тора.

Нерезонансные торы обладают т.н. свойством эргодичности. Обычно, когда говорят об эргодичности, то всегда это понятие связывают со статистическими свойствами динамики многих частиц - атомов и молекул макроскопического объема вещества, где имеет место молекулярный хаос. В статистической физике принятие известной гипотезы об эргодичности позволяет рассматривать ансамбли из очень большого числа частиц с набором непрерывно меняющихся независимых переменных (q, p) вместо аналогичных параметров одной или нескольких единиц частиц, но меняющихся во времени. Тогда произвольный физический параметр, например, давление P можно вычислять как средний импульс одной частицы v об стенку сосуда в течение очень большого времени, но можно вычислять как среднее значение импульса в конкретный момент времени по большому числу частиц с различными скоростями v_i:

.

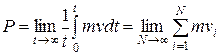Как становится из вышесказанного, простейшая механическая система из двух независимых гармонических осцилляторов может обладать свойством эргодичности. Действительно, допустим мы хотим знать, как часто изображающая точка проходит через выделенный участок тора. Для этого можно проследить за движением этой точки в течение длительного времени. Но можно просто взять распределение траектории изображающей точки по поверхности тора и вычислить площадь заданного на нем участка. Ответ в обоих случаях будет одинаковым.

Как видно, одно из основных свойств систем многих частиц в статистической физике - эргодичность может быть присуще и очень простым механическим системам. Это означает, что эргодичность не является признаком хаотичности, или следствием такой сложной динамики. Как будет видно ниже, даже хаотическая динамика может встречаться в достаточно простых механических системах.

2.2. Хаотическая динамика простых систем. Теорема Колмогорова - Арнольда - Мозера.

Рассмотренными классификациями фазовых поверхностей резонансных и нерезонансных торов возможная динамика механической системы не ограничивается. Существуют относительно простые механические системы, динамика которых не сводится к движению по поверхности торов, т.е. не является ни периодической, ни квазипериодической. Примером такой системы является модель Эно - Хейлеса по имени ее создателей (1964 г). Авторы моделировали движение звезды в среднем поле галактики. После ряда упрощений и учета интегралов движения (т.е. некоторых сохраняющихся физических величин) задача свелась к анализу поведения в четырехмерном фазовом пространстве частицы единичной массы с функцией Гамильтона

.

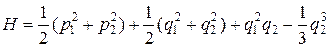Для этой функции Гамильтона есть интеграл энергии H = E, т.е. полная энергия механической системы сохраняется. Если бы система с таким гамильтонианом была полностью интегрируемой, то ее можно было представить или движением по замкнутой поверхности, или топологически эквивалентной ей поверхности тора. В общем случае поверхность тора была бы всюду плотно покрыта фазовыми траекториями, как у системы из двух гармонических осцилляторов.

Модель Эно-Хейлеса содержит только один свободно меняющийся параметр E - полную энергию. При небольших энергиях E динамика такая, что может быть сведена к движению по поверхностям вложенных друг в друга торов, где на каждом из них полная энергия системы остается постоянной величиной.

С ростом энергии E ³ E₀ »0.125 характер движения существенно менялся: некоторые торы сохранялись, но наблюдалась и совершенно новая динамика, в которой часть торов разрушалась и напоминала случайное блуждание изображающей точки в фазовом пространстве. Это также означает случайное или хаотичное блуждание звезды в гравитационном поле галактики. Чтобы более точно пояснить что происходит, предположим, что известно такое преобразование переменных (q_i, p_i) ® (q_*i, p_*i), где q_*i и p_*i - новые переменные, относительно которых функция Гамильтона H представляется в виде суммы из двух частей:

,

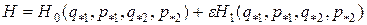где H₀ отвечает динамике с энергией E < E₀; eH₁ - динамике с энергией E > E₀; e = |E - E₀| << 1. Гамильтониан eH₁ играет роль малого возмущения к основной части H₀. Первая часть H₀ отвечает полностью интегрируемой системе, т.е. соответствующая ей динамика может быть представлена движением по поверхности торов, которые при очень малых значениях e устойчивы. Знаменитая теорема Колмогорова-Арнольда-Мозера (КАМ) утверждает, что возмущение eH₁ может привести к разрушению некоторой части первоначально существовавших торов с гамильтонианом H₀ и на их месте возникает нерегулярная динамика, т.е. фактически хаотическое движение (рис. 2.3).

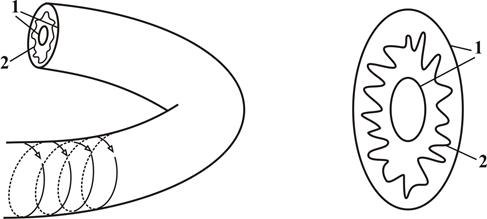
Рис. 2.3. Новая динамика в виде сложной «поверхности» на месте разрушенного тора.

Причем «разрушенные торы» оказываются зажатыми между устойчивыми торами. На этом упрощенном рисунке показан только один из оказавшихся неустойчивым и разрушенным тором (кр. 2), и, как следствие, он располагается между устойчивыми торами большего и меньшего радиусов (кр. 1). Точная формулировка теоремы КАМ сложна, она занимает несколько страниц книжного текста, не говоря о ее доказательстве, поэтому здесь приводится только краткое и основное ее содержание.

Из-за трудности изображения динамики на месте разрушенных торов на рис. 2.3 представлена чрезмерно упрощенная картина. В действительности изображающая точка движется по настолько сложной траектории, что ее невозможно представить в точном виде, получающаяся поверхность из «собранных» траектории не является поверхностью в том смысле, к которому мы привыкли. Ниже свойства такой поверхности будут обсуждаться более подробно. Любопытно следующее: сложная динамика на месте разрушенных торов обладает свойством эргодичности, хотя, как было сказано, энергетической поверхности в обычном понимании уже не существует.

2.3. Свойство перемешивания в хаотической динамике простых систем.

Как было выяснено выше, существуют простые механические системы, динамика которых при определенных условиях (например, малые энергии E) может быть представлена в виде движения по поверхности торов. Но также возможна другая динамика, когда часть торов разрушается и на месте разрушенных торов возникает новая и сложная динамика. Характер такой динамики можно наглядно представить в фазовом пространстве в виде «капли жидкости», постоянно деформирующейся в процессе эволюции механической системы (рис. 2.4).

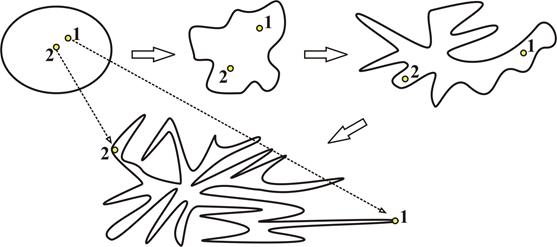
Рис. 2.4. «Перемешивание» фазового объема и разбегание точек 1 и 2.

Начальный «объем», точнее площадь «капли» на этом рисунке - это область допустимых начальных значений координат и импульсов, или область допустимых начальных условий для механической системы. В последующие моменты времени капля деформируется, что означает эволюцию системы. Площадь фигуры, которая принята вначале в виде эллипса, сохраняется, но сильно меняется ее форма. Первоначально близки расположенные две точки 1 и 2 с течением времени сильно удаляются друг от друга. Этот процесс напоминает перемешивание капли краски в воде, откуда и произошло название свойства динамики системы. Такое сильное удаление точек 1 и 2 означает трудность предсказания поведения системы на больших временах ее эволюции, поскольку мало различающиеся вначале координаты и импульсы с течением времени сильно меняются. Иногда такое явление называют «эффектом бабочки» по истории из одного фантастической повести, когда взмах крыла бабочки изменило весь ход истории в далеком будущем. Поскольку фазовые переменные ограничены по численному значению в силу сохранения полной энергии, то за достаточно длительное время образуется некоторая «однородная смесь» из точек, принадлежащих принимаемым значениям q и p, и таких, которые эти переменные не могут принимать. Множество точек, принадлежащих q и p, образуют некоторую «поверхность», подобной той, что изображено на рис. 2.3 на месте разрушенного тора.

Модель Эно-Хейлеса не является единственным примером простой механической системы со сложным поведением, но исторически она появилась первой. Впоследствии были обнаружены и другие системы, например, т.н. «бильярд» Я. Г. Синая (рис. 2.5) открытый советским математиком в 1962 году. Эта механическая система еще проще, чем модель Эно-Хейлеса.

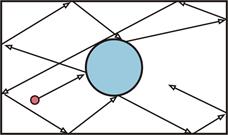
Рис. 2.5. Блуждание шарика в «бильярде» Синая.

В центре прямоугольника расположен неподвижный большой диск, шарик запускают с произвольной начальной скоростью и направлением, впоследствии шарик движется внутри прямоугольника без трения и с диском и стенкой испытывает упругие столкновения. Может показаться, что движение будет периодическим, пусть даже большим. Но строгий анализ показывает существование большого числа начальных направлений движения (очевидно, от модуля скорости тип динамики не зависит), приводящих к сложной динамике, и шарик никогда не возвратится в исходную точку. Эта динамика обладает свойством перемешивания, т.е. хаотична. Нетрудно видеть, что модель Синая напоминает движение молекул в газе: при увеличении дисков и частиц свойство хаотичности только усиливается.

Строго доказано следующее: если динамика обладает свойством перемешивания, то в ней автоматически имеется свойство эргодичности, но наличие эргодичности не означает наличие перемешивания.

Отличительной особенностью хаотической динамики в механических системах с сохраняющимся объемом в фазовом пространстве (рис. 2.4) является постоянство полной энергии, т.е. функции Гамильтона. Можно сказать, что в системах с большим числом степеней свободы n, изображающая точка в фазовом пространстве движется по поверхности многомерного гиперпространства с 2n осями координат q_i, p_i, i = 1, …, n и описываемой уравнением

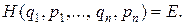
Сохранение фазового объема утверждается теоремой Лиувилля и служит основой для формулировки положений статистической физики.

2.4. Аттрактор динамической системы.

Существует несколько математически строгих определений аттрактора и все они достаточно сложны. Здесь же ограничимся простыми пояснениями, позволяющими на физическом уровне понимать, что такое аттрактор. С простыми аттракторами мы уже встречались, по фазовым портретам «устойчивый фокус» (рис. 1.1б) и «устойчивый узел» (рис. 1.2а) видно, что любая изображающая точка, выбранная в качестве стартовой, с течением времени придет к началу координат. Или, какие бы начальные условия мы ни взяли, рано или поздно система перейдет в состояние покоя. В этом случае говорят об аттракторе, определяемом уравнением x = 0, x¢ = 0. На фазовой траектории это всего одна точка. Становится понятным, что аттрактор – это множество точек, к которому стремятся все близлежащие фазовые траектории в пределе t ® ¥.

а б

Рис. 2.6. Примеры аттракторов: а) в виде линий в 2-мерном пространстве; б) в виде плоскости в 3-мерном пространстве.

В нашем примере это множество состоит из одной точки. Аттрактор может состоять из бесконечного числа точек, т.е. образовывать геометрическую фигуру – линию, поверхность, объем и т.д. Например, фокус тоже может оказаться аттрактором, если фазовый портрет динамической системы будет иметь вид, как показано на рис. 2.6а.

Аттрактор на рис.2а называют еще предельным циклом. Например, для динамической системы

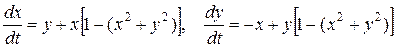
траектория x² + y² = 1 является предельным циклом. Его параметрические уравнения будут

,

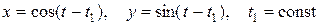а уравнения всех других фазовых траекторий запишутся в виде:

.

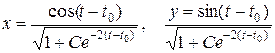Значениям постоянной интегрирования C > 0 соответствуют фазовые траекторий, накручивающиеся на предельный цикл изнутри (при t ® ¥), а значениям -1 < C < 0 - накручивающиеся снаружи.

Аттрактором на рис. 2.6б является поверхность, любая изображающая точка вне этой поверхности с течением времени t ® ¥ будет сколь угодно близко приближать к ней. На рис. 2.6 и других примерах видим, что множество точек аттрактора как бы обладают свойством «притягивать» другие точки фазового пространства. Поэтому аттрактору часто дают определение как о притягивающем множестве точек в фазовом пространстве. Множество точек между устойчивыми торами, к которому стремятся траектории на примере гамильтоновых систем (рис. 2.3), тоже является аттрактором, но оно не сводится к линиям или поверхностям, как на рис. 2.6, а к геометрическим объектам, занимающим место между линией и поверхностью. В последнем случае для демонстрации свойств такого объекта применяют следующий способ (отображение А. Пуанкаре): в фазовом пространстве выбирают (секущую) поверхность S и отмечают на ней точки пересечения фазовых траекторий в течение длительного времени, в идеале – при t ® ¥. После этого изучают геометрические свойства множества точек пересечения. Например, рассмотрим фазовое пространство системы двух осцилляторов (рис. 2.1). В качестве секущей поверхности S возьмем поверхность, перпендикулярной к внешней окружности тора (рис. 2.7).

Точки пересечения на поверхности S последовательно будут формировать окружность радиуса R₂. При малых временах будут различаться только контуры этой окружности, но в пределе t ® ¥, когда траектория изображающей точки всюду плотно покроет поверхность тора, на поверхности S четко вырисуется окружность. Проделав то же самое с траекторией, принадлежащей к хаотической динамике, возникшей на месте разрушенного тора, мы получим некоторое множество точек, которое будет густо и случайным образом покрывать поверхность S и это множество не будет гладкой кривой, подобной окружности. Последовательное разрушение окружности, соответствующей тору и возникновение на ее месте нового множества приведено на рис. 2.8.

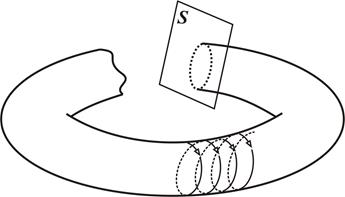
Рис. 2.7.

Рис. 2.8.

В математике любое множество можно характеризовать размерностью, это же можно сделать и для множества точек, оставляемых на поверхности S при выполнении отображения Пуанкаре. Но вначале обратимся к некоторым математическим основам.

2.5. Размерность множества точек аттрактора.

Множество Кантора (1883 г). Для начала проведем следующий математический эксперимент: возьмем отрезок единичной длины [0; 1], разделим его на три равные части и вырежем среднюю из них – интервал (1/3; 2/3). Далее с каждым из оставшихся отрезков поступим точно также. Тогда мы получим последовательность отрезков с геометрической прогрессией убывающей длины (рис. 2.9).

На первом этапе построения имеем один отрезок, на втором – два, на третьем – четыре. На k-м этапе будем иметь N_k = 2^k отрезков, не связанных друг с другом и длиной l_k = 1/3^k каждый. При k ® ¥ общая длина выброшенных отрезков при этом равна единице:

.

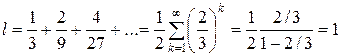Теперь спросим себя: что останется на том месте, где был единичный отрезок? Казалось бы, ничего не останется, но для математической интуиции вопрос будет не простым, поскольку на любом этапе остаются отрезки, пусть даже сколь угодно малой длины. Полученная в результате бесконечного дробления совокупность отрезков называется множеством Кантора, или, пылью Кантора.

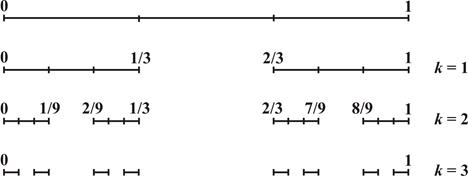
Рис. 2.9. Первые три этапа построения множества Кантора.

Заметим, здесь не обязательно разбивать каждый отрезок на три и притом равные части. Но если кратность деления постоянная, то множество получается масштабно-инвариантным.

Рассмотрим теперь другой классический пример построения масштабно-инвариантного множества. Снова берем отрезок [0; 1] и делим его на три части (рис. 2.10).

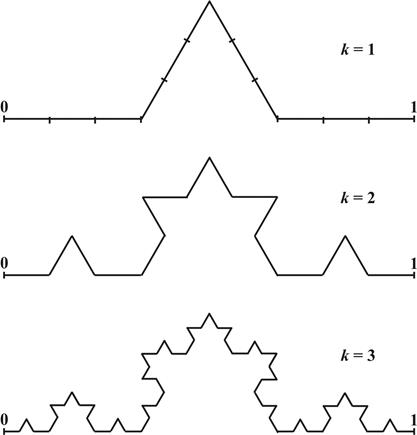
Рис. 2.10. Первые три этапа построения кривой Коха.

Но теперь на месте выброшенной центральной части строим угол со сторонами 1/3, т.е. стороны угла равны длине выброшенной части. Получается ломаная линия, состоящая из отрезков равной длины. Далее проделываем с каждым из его частей-отрезков (k = 2), и так до бесконечности (k = 3, …). На каждом этапе число отрезков N_k растет по геометрической прогрессии, N_k = 4^k. С таким же темпом уменьшается длина каждого отрезка l_k = 1/3^k. Общая длина получающейся кривой L_k растет по закону

.

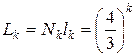При этом надо обратить внимание, что кривая остается в компактной области на плоскости. По мере стремления k ® ¥ кривая как будто обретает толщину и будет представлять нечто между обычной линией и поверхностью. Получающийся геометрический объект называется кривой Коха.

Ковер Серпинского. Еще один пример необычных фигур получается из квадрата. Пусть его стороны равны единице, разделим его на девять равных частей – квадратов со сторонами l₁ = 1/3. Выбросим из них центральный квадрат (рис. 2.11). Это первый этап с k = 1, на втором этапе то же самое проделаем с каждым из оставшихся N₁ = 8 квадратов. На этом втором этапе (k = 2) сторона разбитых квадратов равна l₂ = 1/9 = 1/3². Оставшиеся квадраты образуют закрашенную область, их число N₂ = 64 = 8².

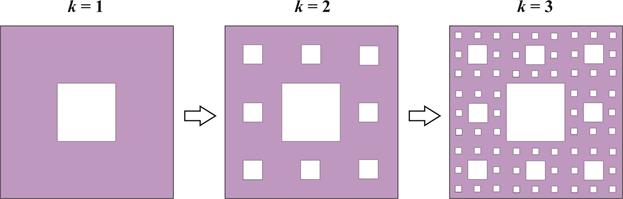
Рис. 2.11.

На третьем этапе (k = 3) получим l₃ = 1/27 = 1/3³, N₃ = 8³. Очевидно, на произвольном k шаге построения l_k = 1/3^k, N_k = 8^k. В пределе k ® ¥ получается всюду дырявый ковер Серпинского, общая площадь выброшенных участков равна нулю и, казалось бы, от ковра ничего не осталось. Этот пример является двумерным аналогом множества Кантора.

Полученные специфические геометрические фигуры характеризуют т.н. фрактальной размерностью d_f. Она определяется следующим образом: рассмотрим в n-мерном пространстве некоторое множество A. Покроем это множество n-мерными кубиками со стороной e так, чтобы эти кубики содержали все точки множества A. Пусть N - минимальное число кубиков, необходимых для покрытия A. Рассмотрим предел

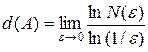. (2.11)

Величина d(A) = d_f является метрической размерностью и емкостью или фрактальной размерностью множества A.

Определим размерность для построенных выше множеств. В случае множества Кантора в качестве кубиков выступают отрезки l_k, необходимое для покрытия множества минимальное их число равно N_k. Предельный переход в (2.11) производится стремлением k ® ¥. Тогда находим

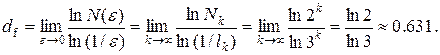
Как и следовало ожидать, 0 < d_f < 1, где 0 - топологическая размерность пустого множества; 1 - топологическая размерность обычной кривой. Таким же образом находим фрактальную ра