Решение произвольных СЛУ

Рассмотрим СЛУ

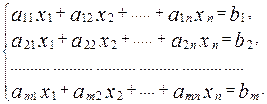(1)

где т ¹ п., такую систему называют «прямоугольной». В этом случае применить матричный метод или правило Крамера невозможно (определитель прямоугольной матрицы не определен). Метод решения прямоугольной системы основан на преобразовании этой системы к равносильной ей системе более простого вида.

Определение 2.

Две СЛУ называются равносильными (эквивалентными), если каждое решение одной из них является решением другой и наоборот.

Перечислим преобразования, которые можно производить над уравнениями СЛУ с целью приведения ее к равносильной системе:

· перестановка местами уравнений в системе; · умножение любого уравнения системы на число, отличное от нуля; · прибавление к обеим частям одного уравнения системы соответствующих частей другого; · отбрасывание уравнения, в котором все коэффициенты при неизвестных и свободный член равны нулю.

(6)

Один из методов решения произвольных систем, называемый методом Гаусса, состоит в том, что с помощью преобразований прямоугольная СЛУ приводится к равносильной ей системе треугольного вида

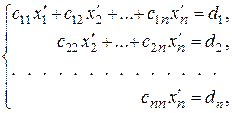(4)

или усеченного треугольного вида (трапециевидной формы)

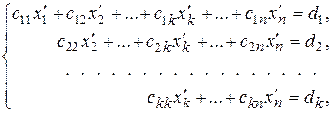(5)

Такие системы легко исследовать и решить. Здесь неизвестные 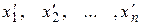– это неизвестные х_1­, х₂, ..., х_п, может быть, переставленные местами, а k £ n, k £ m .

Эти системы специального вида получают так: выбирают какое-либо уравнение и неизвестное 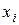в нем, поставив это уравнение и неизвестное на первое место в системе (т.е. считают 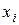= 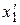), исключают выбранное неизвестное из остальных уравнений, обращая коэффициенты при этом неизвестном в ноль. Затем выбирают неизвестное 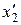, оставляют его в двух первых уравнениях на втором месте и исключают из остальных, и так далее.

Если в результате преобразований получились уравнения вида

0х_к + 0х_к+1 +...+ 0х_n = d , d ¹ 0,

то система несовместна, т.к. никакая совокупность чисел (a₁, a₂, a₃,…, a_п) этому уравнению не удовлетворяет.

Если таких уравнений в преобразованной системе нет, то полученная система (а, следовательно, и исходная) совместна.

Если получена система вида (4), то её решение находят «обратным ходом»: из последнего уравнения находят 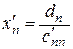, подставляя это значение в предпоследнее уравнение, находят 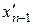, и так далее, вверх по системе, доходят до неизвестного х¢₁.

Если в результате преобразований получилась система вида (5), то поступают следующим образом.

Поскольку число уравнений системы (5) меньше числа неизвестных (k < n), то из этих уравнений можно найти только k неизвестных (коэффициенты при которых образуют отличный от нуля определитель, чаще всего это те, которые занимают первые k мест в уравнениях). Эти неизвестные называют базисными, их оставляют в левой части уравнений системы. Остальные неизвестные называют свободными, их переносят в правую часть уравнений и считают известными, принимающими произвольные значения:

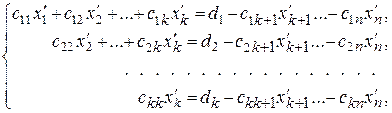
В результате получится система вида (4), из которой «обратным ходом» находят неизвестные 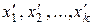как функции свободных неизвестных

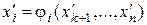
Так как свободным неизвестным можно придавать произвольные значения, то система имеет бесчисленное множество решений, а значит, и исходная система имеет бесчисленное множество решений.

Совокупность

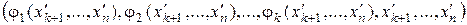
называется общим решением системы (5), и, следовательно, системы (1). Придавая в общем решении свободным неизвестным конкретные числовые значения, будем получать частное решение системы.

Реализация метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Рассмотрим расширенную матрицу`А исходной системы. Легко убедиться в том, что преобразования (6), приводящие систему линейных уравнений к треугольной или трапециевидной форме выполняются, по существу, над строками и столбцами этой матрицы:

§ перестановка строк;

§ умножение любой строки на число, отличное от нуля;

§ прибавление какой-либо строки матрицы, умноженной на число, к другой строке;

§ отбрасывание нулевой строки.

Поэтому вместо преобразований уравнений системы проводят соответствующие преобразования расширенной матрицы этой системы. Такие преобразования называются элементарными преобразованиями матрицы.

Рассмотрим пример. Решить систему методом Гаусса:

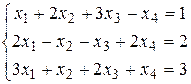
Запишем расширенную матрицу системы и произведем элементарные преобразования над строками этой матрицы:

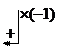
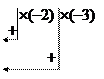
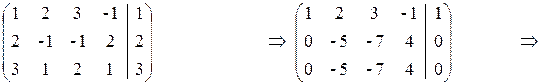
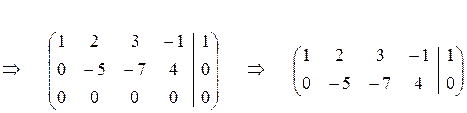
По последней матрице составим систему уравнений, равносильную исходной:

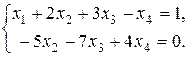
Поскольку в результате преобразований не получилось ни одного уравнения вида

0х_к + 0х_к+1 +...+ 0х_n = b , b ¹ 0,

то полученная система имеет решение. Так как неизвестных в этой системе больше чем уравнений, то разобьем эти неизвестные на базисные и свободные. За базисные возьмем два неизвестных системы, коэффициенты при которых образуют отличный от нуля определитель, это, например, х₁ и х₂ : 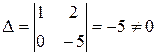. Остальные неизвестные х₃ и х₄ считаем свободными и перенесем их в правые части уравнений системы. Получим систему

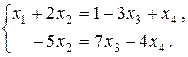
Чтобы записать все множество решений системы (общее решение), положим х₃ = с₁ , х₄ = с₂ , где с₁, с₂ – произвольные действительные числа. Получим

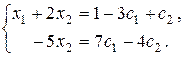
Из второго уравнения этой системы находим

.

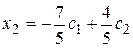Подставляя найденное значение х₂ в первое уравнение, найдем неизвестное х₁:

.

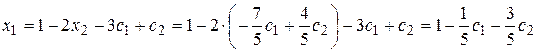Тогда можно записать

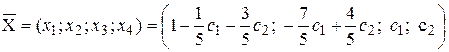, с₁, с₂ ÎR .

Эта матрица-строка и есть общеерешение заданной системы.

Придавая с₁ и с₂ любые числовые значения, можно получать частные решения:

при с₁ = 0, с₂ = 1 получим 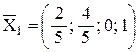– частное решение.

Другой пример. Рассмотрим систему

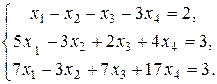
Возьмем расширенную матрицу этой системы и проведем над ней элементарные преобразования:

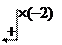
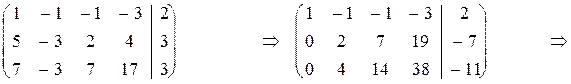
Þ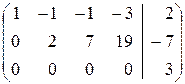

Запишем по полученной матрице систему линейных уравнений

.

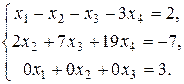Поскольку в результате преобразований получили уравнение вида

0х_к + 0х_к+1 +...+ 0х_n = b , b ¹ 0: ,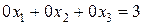

значит, исходная система решений не имеет.

Метод Гаусса является методом исследования и решения системы линейных уравнений. Во многих прикладных вопросах возникает необходимость только исследования системы. Это можно сделать с помощью понятия ранга матрицы системы и теоремы Кронекера-Капелли.