Спектральный анализ сигналов

Любой сигнал x(t) математически может быть представлен набором простейших функций 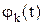(подобно разложению числа на сомножители). Главное требование к простейшим функциям – их единственность (уникальность) и непохожесть на другие функции. Это свойство исключительности набора простейших функций отражается в математике свойством ортогональности: (на некотором интервале (0,Т)):

.

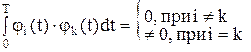Разложение сигнала на простейшие функции представляется рядом:

.

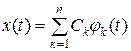Коэффициенты ряда – С_k выбираются из условия минимума среднеквадратичной погрешности по отношению к исходному сигналу:

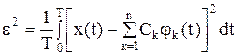
С_k находятся по формуле (с учетом нормировки)

.

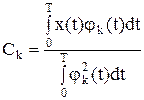При увеличении членов ряда n к бесконечности (∞) погрешность отображения исходной функции x(t) становится сколь угодно малой. Тогда такой ряд называют обобщенным рядом Фурье.

В качестве простейших ортогональных функций часто выбирают тригонометрический ряд:

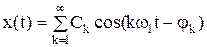. (1.1)

Совокупность коэффициентов ряда {C_k} называют спектром амплитуд или амплитудно-частотным спектром, а совокупность {j_k} - спектром фаз или фазово-частотным спектром. С учетом:

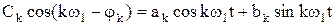(1.2)

и

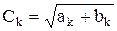
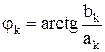
получаем другую форму ряда Фурье:

, (1.3)

где коэффициенты a_k и b_k определяется как:

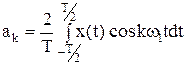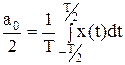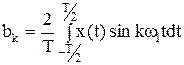; ; . (1.4)

Коэффициенты a_k называют косинусной (четной) составляющей, b_k - синусной (нечетной).

Разложение сигнальной функции на "простейшие" составляющие называют спектральным анализом или спектральным разложением. В тригонометрическом ряде Фурье в качестве "простейшей" функции принято синусоидальное (косинусоидальное) колебание одной частоты, называемое "гармоническим". Поэтому составляющие ряда Фурье называют "гармоники"; имея в виду, что ряд состоит из кратных -k- частот, т.е. кратных гармоник (первая гармоника, вторая гармоника … сотая гармоника …). Так как интервал ортогональности 0,Т – совпадает с периодом Т = 2p/w₁, то определение коэффициентов ряда производится в пределах интервала ортогональности (-Т/2, Т/2).

Рассмотрим пример спектрального разложения периодического колебания типа "меандр". Меандр – греческое слово, обозначающее "орнамент" (рис. 1.3).

а) б)

Рис 1.3

.

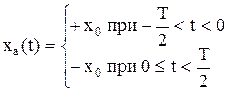
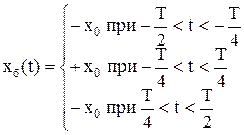Выбор начала координат а) или б) определит состав гармонического разложения: по четным коэффициентам или не четным, это определяется видом функций x(t) в пределах (-Т/2, Т/2). В случае выбора начала координат по а) функция x(t) оказывается нечетной, т.е. х(-Т/2) = -х(Т/2), при этом в ряде Фурье остаются только члены b_k, определяемые нечетной функций синуса. Составляющие a_k оказываются при этом, равными нулю a_k = 0. В случае выбора начала координат по б) функция x(t) оказывается четной, и ряд Фурье будет определяться только составляющими a_k, b_k = 0. Постоянная составляющая, как видно из графика, равна нулю. Для случая а):

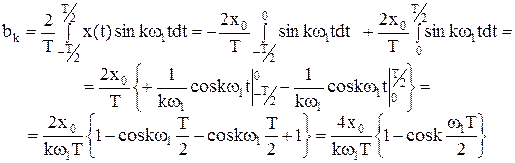
с учетом, что 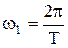и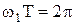

.

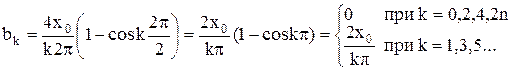Тогда ряд Фурье:

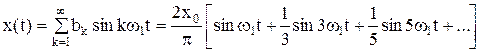
или с учетом w = 2πf

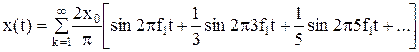. (1.5)

Полученный спектральный состав можно представить графически (рис. 1.4).

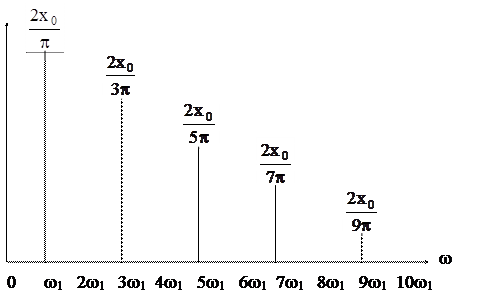Рис. 1.4

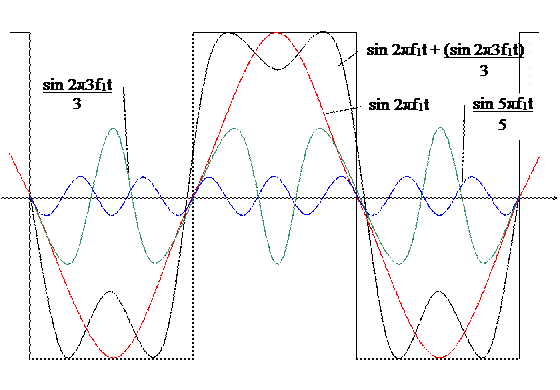Приведенный график называют "спектром". Синтез исходной временной функции по спектральным составляющим понятен из рис. 1.5.

Рис. 1.5