Закон сохранения полной механической энергии системы

До сих пор мы ограничивались рассмотрением поведения одной частицы с энергетической точки зрения. Теперь перейдем к системе частиц. Это может быть любое тело, газ, любой механизм, Солнечная система и т. д.

В общем случае частицы системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. Систему частиц, на которую не действуют никакие посторонние тела или их воздействие пренебрежимо мало, называют замкнутойили изолированной. Понятие замкнутой системы является естественным обобщением понятия изолированной материальной точки и играет важную роль в физике.

Введем понятие потенциальной энергии системы частиц. Рассмотрим замкнутую систему, между частицами которой действуют только центральные силы, т. е. силы, зависящие при данном характере взаимодействия только от расстояния между ними и направленные по прямой, их соединяющей.

Покажем, что в любой системе отсчета работа всех этих сил при переходе системы частиц из одного положения в другое может быть представлена как убыль некоторой функции, зависящей при данном характере взаимодействия только от конфигурации самой системы или от относительного расположения ее частиц. Эту функцию назовем собственнойпотенциальной энергией системы, в отличие от внешней потенциальной энергии, характеризующей взаимодействие данной системы с другими телами.

Первоначально рассмотрим систему из двух частиц. Вычислим элементарную работу сил, с которыми эти частицы взаимодействуют между собой. Пусть в произвольной системе отсчета в некоторый момент времени положение частиц определяется радиус-векторами 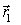и . Если за время dt частицы совершили перемещения 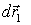и соответственно, то работа сил взаимодействия и F₂₁равна

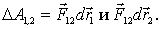
Теперь учтем, что, согласно третьему закону Ньютона , поэтому предыдущее выражение можно переписать так:

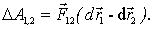
Введем вектор 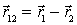, характеризующий положение 1-й частицы относительно 2-й. Тогда 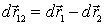и после подстановки в выражение для работы получим

.

Сила 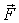- центральная, поэтому работа этой силы равна убыли потенциальной энергии взаимодействия данной пары частиц, т. е.

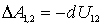
Так как функция зависит только от расстояния 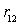между частицами, то ясно, что работа не зависит от выбора системы отсчета.

Теперь рассмотрим систему из трех частиц, так как полученный в этом случае результат легко обобщить и на систему из произвольного числа частиц. Элементарная работа, которую совершают все силы взаимодействия при элементарном перемещении всех частиц, может быть представлена как сумма элементарных работ всех трех пар взаимодействий, т. е.

Но для каждой пары взаимодействий, как было показано 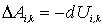, поэтому

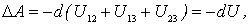
где функция 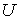есть собственная потенциальная энергияданной системы частиц:

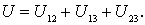
Так как каждое слагаемое этой суммы зависит от расстояния между соответствующими частицами, то очевидно, что собственная потенциальная энергия U данной системы зависит от относительного расположения частиц в один и тот же момент времени, или, другими словами, от конфигурации системы.

Ясно, что подобные рассуждения справедливы и для системы из любого числа частиц. Поэтому можно утверждать, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия U, и работа всех центральных внутренних сил при изменении конфигурации системы равна убыли собственной потенциальной энергии системы, т. е.

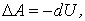
(4.10)

а при конечном перемещении всех частиц системы

(4.11)

где 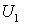и 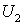-значения потенциальной энергии системы в начальном и конечном состояниях.

Собственная потенциальная энергия системы U - величина неаддитивная, т. е. она не равна в общем случае сумме собственных потенциальных энергий ее частей. Необходимо учесть еще потенциальную энергию взаимодействия 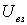отдельных частей системы

,

(4.12)

где 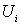- собственная потенциальная энергия части системы.

Следует также иметь в виду, что собственная потенциальная энергия системы, как и потенциальная энергия взаимодействия каждой пары частиц, определяется с точностью до прибавления произвольной постоянной, которая, впрочем, и здесь совершенно несущественна.

В заключение приведем полезные формулы для расчета собственной потенциальной энергии системы. Прежде всего покажем, что эта энергия может быть представлена как.

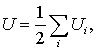
(4.13)

где 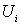- потенциальная энергия взаимодействия частицы со всеми остальными частицами системы. Здесь сумма берется по всем частицам системы.

Убедимся в справедливости этой формулы сначала для системы из трех частиц. Выше было показано, что собственная потенциальная энергия данной системы 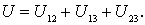Преобразуем эту сумму следующим образом. Представим каждое слагаемое 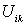в симметричном виде: 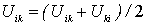, ибо ясно, что 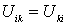. Тогда

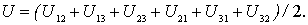
Сгруппируем члены с одинаковым первым индексом:

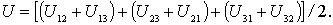
Каждая сумма в круглых скобках представляет собой потенциальную энергию 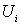взаимодействия частицы с остальными двумя. Поэтому последнее выражение можно переписать так:

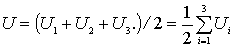
что полностью соответствует формуле (5.38). Обобщение полученного результата на произвольную систему очевидно, ибо ясно, что подобные рассуждения совершенно не зависят от числа частиц, составляющих систему.

Найдем элементарную работу, которую совершают все силы, действующие на все частицы системы:

,

где - суммарная кинетическая энергия системы. Заметим, что кинетическая энергия системы - величина аддитивная: она равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они между собой или нет.

Итак, приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. При элементарном перемещении всех частиц

(4.14)

а при конечном перемещении

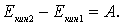
(4.15)

Уравнение (4.15) можно представить и в другой форме, поделив обе части его на соответствующий промежуток времени dt. Имея при этом в виду что, получим

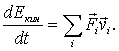
(4.16)

т. е. производная кинетической энергии системы по времени равна суммарной мощности всех сил, действующих на все частицы системы,

Уравнения (4.6) - (4.15) справедливы как в инерциaльных, так и в неинерциальных системах отсчета. Следует только понимать, что в неинерциальных системах кроме работы сил взаимодействия необходимо учитывать и работу сил инерции.

Проведем классификацию сил по их свойствам. Известно, что частицы рассматриваемой системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. В соответствии с этим силы взаимодействия между частицами системы называют внутренними, а силы, обусловленные действием других тел, не входящих в данную систему, - внешними. В неинерциальной системе отсчета к последним нужно относить и силы инерции.

Кроме того, все силы делят на потенциальные и непотенциальные. Потенциальными называют силы, зависящие при данном характере взаимодействия только от конфигурации механической системы. Работа этих сил, как было показано, равна убыли потенциальной энергии системы.

К непотенциальным силам относятся так называемые диссипативные силы - это силы трения и сопротивления, а также энергетическиесилы, вызывающие увеличение механической энергии системы за счет других видов энергии (например, взрыв артиллерийского снаряда). Важной особенностью данных сил является то, что суммарная работа внутренних диссипативных сил рассматриваемой системы отрицательна, а энергетических сил - положительна, причем в любой системе отсчета.

Теперь учтем, что работа внутренних потенциальных сил равна убыли собственной потенциальной энергии системы, т.е.

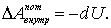
Тогда предыдущее выражение примет вид

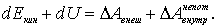
(4.17)

Введем понятие полной механической энергии системы, или, короче, механической энергии, как сумму кинетической и потенциальной энергии системы:

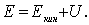
(4.18)

Очевидно, энергия Е зависит от скоростей частицы системы, характера взаимодействия между ними и конфигурации системы. Кроме того, энергия Е, как и потенциальная энергия U, определяется с точностью до прибавления несущественной произвольной постоянной и является величиной , т. е. энергия Е системы не равна в общем случае сумме энергий ее отдельных частей. В соответствии c (4. 5)

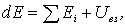
(4.19)

где 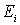- механическая энергия части системы, 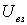- потенциальная энергия взаимодействия ее отдельных частей.

Вернемся к формуле (4.17). Перепишем ее с учетом (4.18) в виде

(4.20)

Это выражение справедливо при бесконечно малом изменении конфигурации системы. При конечном же изменении

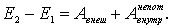
(4.21)

т. е. приращение механической энергии системы равно алгебраической сумме работ всех внешних сил и всех внутренних непотенциальных сил.

Уравнение (4.20) можно представить и в другой форме, поделив обе части его на соответствующий промежуток времени dt. Тогда

.

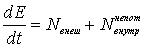(4.22)

т. е. производная механической энергии системы по времени равна алгебраической сумме мощностей всех внешних сил и всех внутренних непотенциальных сил.

Уравнения (4.20) - (4.22) справедливы как в инерциальной, так и в неинерциальной системах отсчета. Следует только иметь в виду, что в неинерциальной системе отсчета необходимо учитывать работу (мощность) и сил инерции, играющих роль внешних сил, т. е. под 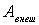надо понимать алгебраическую сумму работ внешних сил взаимодействия и работу сил инерции .

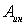Итак, мы пришли к важному результату: механическая энергия системы может изменяться под действием как внешних сил, так и внутренних непотенциальных сил (точнее говоря, под действием алгебраической суммы работ всех этих сил). Отсюда непосредственно вытекает и другой важный вывод - закон сохранения механической энергии: