Общая схема решения уравнения методом итераций

1. Выполнить отделение корней. Выбрать тот корень, который подлежит уточнению, и соответствующий ему отрезок [a; b], содержащий этот корень и не содержащий других корней данного уравнения.

2. Преобразовать уравнение (1) к равносильному ему уравнению вида (9).

3. Найти 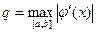и проверить, является ли функция φ(x) сжимающей на отрезке [a; b].

4. Если сжимаемость имеет место, то:

4.1 задаться точностью ξ нахождения приближенного значения корня;

4.2 задаться первым членом итерационной последовательности х₀ – начальным приближением к корню;

4.3 построить следующий член итерационной последовательности (10);

4.4 всякий раз, получив очередной член итерационной последовательности, проверять, выполняется ли условие, следующее из (8):

или (n = 0, 1, 2,…); (13)

4.5 если условие (13) выполняется, то принять х_n, за результат, иначе вновь выполнить пункт 4.3.

Способ перехода от уравнения в форме (1) к равносильному уравнению в форме (9) (и связанный с этим вид функции φ(х)) является определяющим для сходимости итерационной последовательности. Если подбирать φ(х) вслепую, можно впустую потратить массу времени. Однако есть общие приемы, которые позволяют избежать этой ситуации.

Рассмотрим простейший из них. Преобразуем уравнение (1) к равносильному уравнению

х = х - μ · f(x), (14)

где μ - отличная от нуля константа.

Таким образом, φ(x) = х - μ · f(x). Условие (11) приобретает вид

(15)

Если удастся подобрать значение μ так, чтобы условие (15) выполнялось, то метод итераций применим.

Пусть на [a; b] существует единственный корень уравнения f(x) = 0. Будем считать функцию f(х) дифференцируемой на отрезке [a; b] и сохраняющей на этом отрезке свой знак (фактически предполагается, что отрезок достаточно мал).

Рассмотрим вначале случай, когда . Полагая

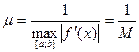, (16)

получим из (14) итерационную формулу:

(17)

Рассмотрим критерий выхода из итерационного процесса:

= = .

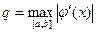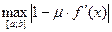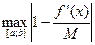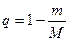Т.к. , то , где .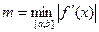

В случае, когда 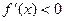, путем аналогичных рассуждений получим: и итерационную формулу:

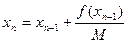(18)

Одним из важнейших свойств итерационных методов решения уравнений, является свойство самоисправляемости. Поскольку начальное приближение х₀ выбирается произвольно, то отсюда следует, что полученное в итерационном процессе n-е приближение при желании можно считать начальным. Это означает, что если в процессе вычисления приближений допускались ошибки, то они не влияют на окончательный результат (при условии, что запрашиваемая точность результата существенно ниже реализуемого в процессе счета уровня точности представления числовых данных). Указанное свойство метода итераций делает его одним из самых надежных методов решения уравнений.