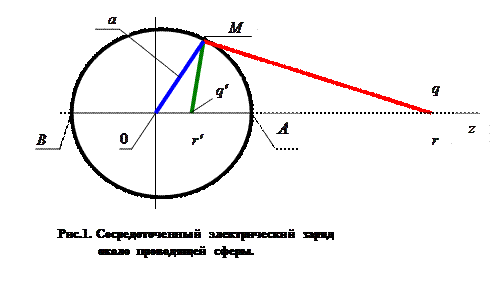
Сосредоточенный электрический заряд около проводящей сферы.

Допустим, что центр проводящей сферы радиуса а находится в начале сферической системы координат, сосредоточенный электрический заряд 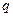помещён на расстоянии 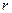от центра сферы ( . Ось симметрии задачи, естественно, проходит через центр сферы и точку расположения исходного электрического заряда. Потенциал электростатического поля рассматриваемой системы должен удовлетворять уравнению Лапласа вне проводящей сферы (кроме точки расположения сосредоточенного заряда), сохранять постоянное значение на поверхности сферы и убывать до нуля в точках пространства, достаточно удалённых от рассматриваемой физической системы.

Сначала рассмотрим случай «заземлённой» сферы, потенциал которой можно положить равным нулю. В этой ситуации оказывается полезным метод изображений, но поскольку поверхность сферы не является плоскостью, использование метода изображений имеет свои особенности.

Пусть на оси симметрии задачи внутри сферической поверхности на расстоянии 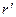от центра сферы помещён фиктивный сосредоточенный заряд 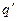, знак фиктивного заряда противоположен знаку исходного сосредоточенного заряда. Подберём величины 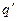и 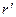таким образом, чтобы удовлетворялись граничные условия для суммарного потенциала электростатического поля. Итак, на поверхности сферы потенциал должен быть равен нулю. Запишем это условие для точек А и В, показанных на рис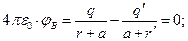. 1:

(1)

При записи этих уравнений учтено различие в знаках исходного и фиктивного электрических зарядов. Из описанной системы уравнений следует промежуточный результат

(2)

и окончательный результат

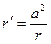или . (3)

Заметим, что если 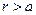, то с необходимостью выполнено условие , т.е. фиктивный заряд необходимо расположить внутри проводящей сферы. Величина фиктивного заряда определяется выражением:

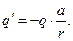(4)

Из этой зависимости следует, что абсолютная величина фиктивного заряда меньше, чем абсолютная величина исходного заряда (напомним, что в случае проводящей плоскости абсолютные величины исходного и фиктивного заряда совпадали).

Непосредственным вычислением можно убедиться, что потенциал электростатического поля, образованного исходным сосредоточенным зарядом и фиктивным сосредоточенным зарядом, обращается в нуль в произвольной точке поверхности сферы.

Напомним, что расстояние между двумя точками пространства, если их положение описано соответствующими радиус-векторами, определено как модуль разности упомянутых радиус-векторов. В декартовой системе координат выражение для модуля вектора известно. При использовании сферической системы координат сначала выписывают все декартовы проекции вектора через сферические переменные, потом записывают выражение для модуля вектора.

Потенциал произвольной точки пространства со сферическими координатами 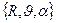, для системы сосредоточенных зарядов рис.1 (заряд и фиктивный заряд) определяется зависимостью:

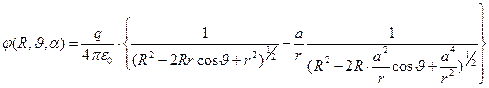. (5)

Проявлением условий симметрии является независимость потенциала результирующего поля от угловой координаты 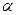. Первое слагаемое в фигурных скобках зависимости (5) обусловлено действием исходного заряда, а второе – действием фиктивного заряда. Относительную величину искажения потенциала поля исходного электрического заряда из-за наличия в начале координат заземлённой проводящей сферы можно оценить выражением

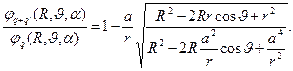(6)

В точках пространства, достаточно удалённых от исходного электрического заряда и проводящей сферы выполняются условия

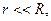
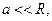
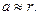(7)

Асимптотическое разложение относительной величины искажения (6) имеет вид:

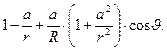(8)

В отличие от рассмотренного выше случая (заряд над проводящей плоскостью) потенциал результирующего поля сохранил асимптотику 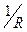при 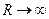, это объясняется тем, что сумма исходного и фиктивного заряда в рассматриваемом случае не равна нулю.

Потенциал реального поля внутри проводящей заземлённой сферы равен нулю вследствие известного принципа максимума для задачи Дирихле для уравнения Лапласа: максимум модуля потенциала внутри области не может быть больше максимального значения модуля потенциала на границе области.

Составляющие напряжённости электростатического поля вне заземлённой проводящей сферы определяются с помощью соответствующих составляющих градиента потенциала в сферической системе координат:

, (9)

(10)

Непосредственным вычислением можно показать, что на поверхности заземлённой проводящей сферы составляющая напряжённости 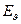обращается в нуль, а радиальная составляющая напряжённости 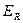зависит от угловой координаты .

С помощью соотношения для нормальных компонент напряжённости электростатического поля на поверхности, несущей поверхностную плотность индуцированных электрических зарядов, получаем зависимость: 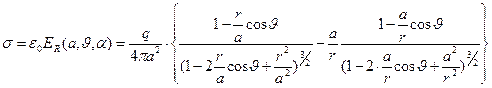(12)

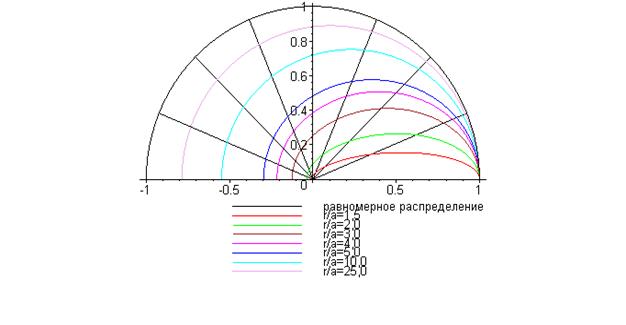
На рис. 2 горизонтальная координата представляет собой полярную ось сферической системы координат, она проходит через центр проводящей сферы и точечный заряд вне сферы. Радиальные направления проведены с интервалом радиан значений угловой координаты . Семейство кривых линий представляет собой изображение зависимости 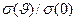, которая является характеристикой неравномерности распределения индуцированного заряда по поверхности сферы. Рассматриваемая конкретная индикатриса распределения поверхностной плотности индуцированного заряда параметрически зависит от величины отношения радиальной координаты 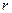заряда 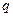к радиусу проводящей сферы 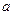. На рис. 2 можно видеть, что с увеличением расстояния исходного электрического заряда 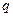от проводящей заземлённой сферы (увеличение отношения r/a) индуцированный заряд всё более равномерно распределяется по поверхности сферы: отношение 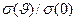приближается к единице. При конечном значении отношения электрический пробой наиболее вероятен для точки проводящей сферы с угловой координатой =0: в этой точке самая большая величина напряжённости электростатического поля.

Интересно, какой суммарный электрический заряд находится на заземлённой проводящей сфере? Проинтегрируем зависимость (12) по поверхности сферы:

(13)

Заряд сферы, оказывается, равен фиктивному заряду, при этом величина фиктивного заряда обратно пропорциональна отношению .

Рассмотрим случай изолированной (незаземлённой) проводящей сферы. Допустим, что первоначально на сфере отсутствовал электрический заряд. Если в произвольную точку пространства вне сферы внесён сосредоточенный электрический заряд 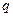, то под действием его поля на поверхности проводящей сферы может произойти перераспределение электрического заряда, а его суммарная величина должна остаться неизменной. Определение электростатического поля в рассматриваемом случае можно провести, используя полученные выше результаты по расчету поля в случае заземленной сферы. Оказывается, достаточно в центре сферы дополнительно поместить второй фиктивный электрический заряд, величина которого равна величине фиктивного заряда 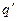в предыдущей задаче, а знак заряда изменен на противоположный. Потенциал произвольной точки пространства вне изолированной проводящей сферы равен сумме потенциалов исходного заряда, первого фиктивного заряда и второго фиктивного заряда. Анализ параметров рассматриваемой электростатической системы проводится аналогично анализу предыдущего случая.