Метрические соотношения в косоугольных системах координат.
Квадрат длины радиус-вектора 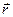 можно получить скалярным произведением
можно получить скалярным произведением 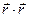 . Воспользуемся при этом тремя возможностями:
. Воспользуемся при этом тремя возможностями:
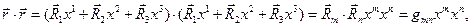 (1)
(1)
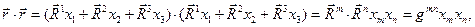 (2)
(2)
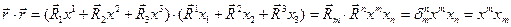 . (3)
. (3)
Полученные результаты удобно объединить
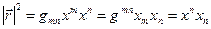 . (4)
. (4)
В общем случае криволинейных координат соотношение (4) справедливо для соответствующих дифференциалов:
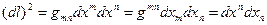 . (5)
. (5)
Говорят, что тензор 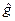 (пока для нас – объект с двумя индексами) в ковариантном или контравариантном представлении (т.е.
(пока для нас – объект с двумя индексами) в ковариантном или контравариантном представлении (т.е. 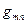 или
или 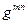 ) определяет «метрику пространства» - устанавливает связь между приращениями координат и расстоянием между рассматриваемыми точками пространства, поэтому этот тензор называют метрическим тензором. Заметим, что его фундаментальное свойство (установление связи между контравариантными и ковариантными координатами) остаётся в силе.
) определяет «метрику пространства» - устанавливает связь между приращениями координат и расстоянием между рассматриваемыми точками пространства, поэтому этот тензор называют метрическим тензором. Заметим, что его фундаментальное свойство (установление связи между контравариантными и ковариантными координатами) остаётся в силе.
Если ковариантный метрический тензор имеет вид
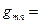
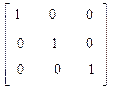 , (6)
, (6)
координатная система является ортогональной и нормированной (ортонормированной). Поясним смысл этого определения. Орты координатных направлений такой системы координат взаимно перпендикулярны, а значение «координаты» вдоль любого из координатных направлений совпадает с расстоянием от начала координат до проекции конца радиус-вектора на рассматриваемое координатное направление. Декартова система координат является примером ортонормированной системы координат.
Если диагональные элементы тензора 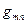 отличны от единицы, не обязательно равны друг другу, а внедиагональные члены равны тождественно нулю, такая система координат является ортогональной, но ненормированной:
отличны от единицы, не обязательно равны друг другу, а внедиагональные члены равны тождественно нулю, такая система координат является ортогональной, но ненормированной:
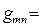
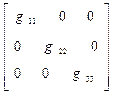 . (7)
. (7)
В этом случае направляющие векторы 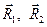 и
и 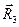 взаимно перпендикулярны, расстояние от начала координат до проекции конца радиус-вектора на рассматриваемое координатное направление не совпадает с соответствующей координатой, выражение для этого расстояния приведено ниже (9).
взаимно перпендикулярны, расстояние от начала координат до проекции конца радиус-вектора на рассматриваемое координатное направление не совпадает с соответствующей координатой, выражение для этого расстояния приведено ниже (9).
Ковариантный метрический тензор вида
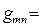
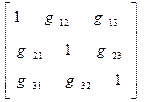 (8)
(8)
описывает нормированную, но не ортогональную систему координат. Представляем читателю самостоятельно выяснить смысл приведённого определения.
В декартовой системе координат контравариантный метрический тензор совпадает с ковариантным метрическим тензором (6), поскольку матрица, обратная к единичной матрице, сама является единичной. Только в этой системе координат справедлива известная теорема Пифагора.
Общее выражение (5) для квадрата элемента длины в произвольной системе координат позволяет вычислить длины элементарных отрезков вдоль координатных направлений исходной системы координат
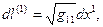
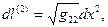
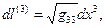 (9)
(9)
и вдоль координатных направлений взаимной системы координат
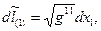
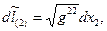
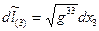 . (10)
. (10)
Таким образом, вектор 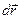 можно описать ещё и с помощью «физических» составляющих одинаковой размерности того или иного строения. В ортогональных криволинейных системах координат физические составляющие разного строения с одинаковым значением индекса ещё и совпадают между собой по величине. Физические представления вектора не обладают свойствами координатных представлений вектора, в частности для них правило преобразования компонент отличается от правила преобразования координат при переходе от одной системы координат к другой. Для теоретических вычислений особенно удобны координатные представления. После их завершения следует, если необходимо, переходить к физическим представлениям, как более наглядным и привычным.
можно описать ещё и с помощью «физических» составляющих одинаковой размерности того или иного строения. В ортогональных криволинейных системах координат физические составляющие разного строения с одинаковым значением индекса ещё и совпадают между собой по величине. Физические представления вектора не обладают свойствами координатных представлений вектора, в частности для них правило преобразования компонент отличается от правила преобразования координат при переходе от одной системы координат к другой. Для теоретических вычислений особенно удобны координатные представления. После их завершения следует, если необходимо, переходить к физическим представлениям, как более наглядным и привычным.
Дата добавления: 2017-09-01; просмотров: 1235;










