Расстояние как интеграл

Обсудим теперь обратную проблему. Пусть вместо таблицы расстояний нам дана таблица скоростей в различные моменты времени, начиная с нуля. В табл. 8.4 представлена зависимость скорости падающего шара от времени. Аналогичную таблицу можно составить и для машины, если записывать показания спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины в любой момент времени, вычислить расстояние, которое ею было пройдено?

Таблица 8.4 • скорость падающего шара

Эта задача обратна той, которую мы только что рассмотрели. Как же решить ее, если скорость машины непостоянна, если она то ускоряется до 90 км/час, то замедляется, затем где-то останавливается у свето­фора и т.д.? Сделать это нетрудно. Нужно использовать ту же идею и выражать полное расстояние через бесконечно малые его части. Пусть в первую секунду скорость будет v₁ , тогда по формуле Ds= v₁Dtможно вычислить расстояние, пройденное за эту секунду. В следующую секунду скорость будет несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние, пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца пути. В ре­зультате мы получим много маленьких отрезков, которые в сум­ме дадут весь путь. Таким образом, путь является суммой ско­ростей, умноженных на отдельные интервалы времени, или s = SvDt,где греческая буква S (сигма) означает сумми­рование. Точнее, это будет сумма скоростей в некоторые мо­менты времени, скажем t_i , умноженные на Dt:

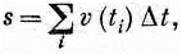
(8.6)

причем каждый последующий момент t_i+1 находится по пра­вилу t_i+1=t_i+Dt. Но расстояние, полученное этим методом, не будет точным, поскольку скорость за время Dtвсе же изменяет­ся. Выход из этого положения заключается в том, чтобы брать все меньшие и меньшие интервалы Dt, т. е. разбивать время дви­жения на все большее число все меньших отрезков. В конце концов мы придем к следующему, теперь уже точному выра­жению для пройденного пути:

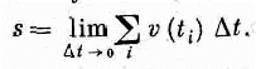
(8.7)

Математики придумали для этого предела, как и для диф­ференциала, специальный символ. Значок D превращается в d, напоминая о том, что интервал времени сколь угодно мал, а знак суммирования превращается в ∫ — искаженное большое S, первая буква латинского слова «Summa». Этот значок назван интегралом. Таким образом, мы пишем

s=∫v(t)dt, (8.8)

где v(t) — скорость в момент t. Сама же операция суммирования этих членов называется интегрированием. Она противополож­на операции дифференцирования в том смысле, что производная этого интеграла равна v(t), так что один оператор (d/dt) «уничто­жает» другой (∫). Это дает возможность получать фор­мулы для интегралов путем обращения формул для дифферен­циалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет равен функции, стоящей в левой колонке. Диф­ференцируя все виды функций, вы сами можете составить таблицу интегралов.

Любая функция, заданная в аналитическом виде, т. е. вы­ражающаяся через комбинацию известных нам функций, диф­ференцируется очень просто — вся операция выполняется чис­то алгебраически, и в результате мы всегда получаем какую-то известную функцию. Однако интеграл не от всякой функции можно записать в аналитическом виде. Разумеется, для каж­дого частного интеграла всегда сначала пытаются найти такую функцию, которая, будучи продифференцирована, давала бы функцию, стоящую после знака интеграла (она называется подынтегральной). Однако это не всегда удается сделать. В та­ких случаях интеграл вычисляют просто суммированием, т. е. вычисляют суммы типа (8.6) со все меньшими и меньшими ин­тервалами, пока не получат результат с достаточной точностью.

Ускорение

Следующий шаг на пути к уравнениям движения — это вве­дение величины, которая связана с изменением скорости дви­жения. Естественно спросить: а как изменяется скорость дви­жения? В предыдущих главах мы рассматривали случай, когда действующая сила приводила к изменению скорости. Бывают легковые машины, которые набирают с места за 10 сек скорость 90 км/час. Зная это, мы можем определить, как изменяется скорость, но только в среднем. Займемся следующим более сложным вопросом: как узнать быстроту изменения скорости. Другими словами, на сколько метров в секунду изменяется скорость за 1 сек. Мы уже установили, что скорость падающего тела изменяется со временем по формуле v=9,8t (см. табл. 8.4), а теперь хотим выяснить, насколько она изменяется за 1 сек. Эта величина называется ускорением.

Таким образом, ускорение определяется как быстрота изме­нения скорости. Всем сказанным ранее мы уже достаточно под­готовлены к тому, чтобы сразу записать ускорение в виде производной от скорости, точно так же как скорость записы­вается в виде производной от расстояния. Если теперь продиф­ференцировать формулу v=9,8 t, то получим ускорение падаю­щего тела

a=dv/dt=9,8. (8.9)

(При дифференцировании этого выражения использовался ре­зультат, полученный нами раньше. Мы видели, что производная от Bt равна просто В (постоянной). Если же выбрать эту по­стоянную равной 9,8, то сразу находим, что производная от 9,8 t равна 9,8.) Это означает, что скорость падающего тела по­стоянно возрастает на 9,8 м/сек за каждую секунду. Этот же результат можно получить и из табл. 8.4. Как видите, в случае падающего тела все получается довольно просто, но ускорение, вообще говоря, непостоянно. Оно получилось постоянным толь­ко потому, что постоянна сила, действующая на падающее тело, а по закону Ньютона ускорение должно быть пропорциональ­но силе.

В качестве следующего примера найдем ускорение в той задаче, с которой мы уже имели дело при изучении скорости:

s=At³+Bt+C.

Для скорости v—ds/dt мы получили формулу

v=3At²+B.

Так как ускорение — это производная скорости по времени, то для того, чтобы найти его значение, нужно продифференци­ровать эту формулу. Вспомним теперь одно из правил табл. 8.3, а именно что производная суммы равна сумме производных. Чтобы продифференцировать первый из этих членов, мы не будем проделывать всю длинную процедуру, которую делали раньше, а просто напомним, что такой квадратичный член встречался нам при дифференцировании функции 5t², причем в результате коэффициент удваивался, a t² превращалось в t. Вы можете сами убедиться в том, что то же самое произойдет и сейчас. Таким образом, производная от ЗAt² будет равна 6Аt. Перейдем теперь к дифференцированию второго слагаемого. По одному из правил табл. 8.3 производная от постоянной бу­дет нулем, следовательно, этот член не даст в ускорение ника­кого вклада. Окончательный результат: a=dv/dt=6At.

Выведем еще две полезные формулы, которые получаются интегрированием. Если тело из состояния покоя движется с постоянным ускорением g, то его скорость v в любой момент времени t будет равна

v=gt,

а расстояние, пройденное им к этому моменту времени,

s=¹/₂gt².

Заметим еще, что поскольку скорость — это ds/dt, а ускоре­ние — производная скорости по времени, то можно написать

Так что теперь мы знаем, как записывается вторая произ­водная.

Существует, конечно, и обратная связь между ускорением и расстоянием, которая просто следует из того, что a=dv/dt. Поскольку расстояние является интегралом от скорости, то оно может быть найдено двойным интегрированием ускорения.

Все предыдущее рассмотрение было посвящено движению в одном измерении, а теперь мы коротко остановимся на движе­нии в пространстве трех измерений. Рассмотрим движение частицы Р в трехмерном пространстве. Эта глава началась с об­суждения одномерного движения легковой машины, а именно с вопроса, на каком расстоянии от начала движения находится машина в различные моменты времени. Затем мы обсуждали связь между скоростью и изменением расстояния со временем и связь между ускорением и изменением скорости. Давайте в той же последовательности разберем движение в трех измерениях. Проще, однако, начать с более наглядного двумерного случая, а уж потом обобщить его на случай трех измерений. Нарисуем две пересекающиеся под прямым углом линии (оси координат) и будем задавать положение частицы в любой момент времени расстояниями от нее до каждой из осей. Таким образом, положе­ние частицы задается двумя числами (координатами) х и у, каж­дое из которых является соответственно расстоянием до оси у и до оси х (фиг. 8.3). Теперь мы можем описать движение, составляя, например, таблицу, в которой эти две коорди­наты заданы как функции времени. (Обобщение на трех­мерный случай требует введения еще одной оси, перпендикулярной двум первым, и измерения еще одной координаты г. Однако теперь расстояния берутся не до осей, а до координат­ных плоскостей.) Как определить скорость частицы? Для этого мы сначала найдем составляющие скорости по каждому направ­лению, или ее компоненты. Горизонтальная составляющая ско­рости, или x-компонента, будет равна производной по времени от координаты х, т. е.

v_x=dx/dt (8.11)

а вертикальная составляющая, или y-компонента, равна

v_y=dy/dt (8.12)

В случае трех измерений необходимо еще добавить

v_z=dz/dt. (8.13)

Как, зная компоненты скорости, определить полную ско­рость в направлении движения? Рассмотрим в двумерном случае два последовательных положения частицы, разделенных корот­ким интервалом времени Dt = t₂-t₁и расстоянием Ds. Из фиг. 8.3 видно, что

(Значок » соответствует выражению «приблизительно равно».)

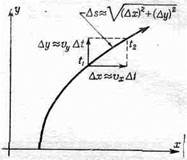
Фиг. 8.3. Описание движения тела на плоскости и вычисление его скорости.

Средняя скорость в течение интервала Dt получается простым делением: Ds/Dt. Чтобы найти точную скорость в момент t, нужно, как это уже делалось в начале главы, устремить Dt к нулю. В результате оказывается, что

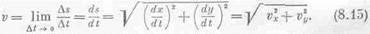
В трехмерном случае точно таким же способом можно полу­чить

Ускорения мы определяем таким же образом, как и скорости: x-компонента ускорения а_х определяется как производная от x-компоненты скорости v_x (т. е. a_x=d²x/dt² — вторая производ­ная по времени) и т. д.

Давайте рассмотрим еще один интересный пример смешан­ного движения на плоскости. Пусть шарик движется в горизон­тальном направлении с постоянной скоростью u и в то же время падает вертикально вниз с постоянным ускорением g. Что это за движение? Так как v_x=dxldt=u и, следовательно, скорость v_x постоянна, то

x=ut, (8.17)

а поскольку ускорение движения вниз постоянно и равно -g, то координата у падающего шара дается формулой

y= -¹/₂gt². (8.18)

Какую же кривую описывает наш шарик, т. е. какая связь между координатами x и y? Из уравнения (8.18), согласно (8.17), можно исключить время, поскольку t=x/u, после чего находим

y=-(g/2u²)x² (8.19)

Эту связь между координатами х и у можно рассматривать как уравнение траектории движения шарика. Если изобразить ее графически, то получим кривую, которая называется параболой (фиг. 8.4).

Фиг. 8.4. Парабола, которую описывает падающее тело, бро­шенное с горизонтальной началь­ной скоростью.

Так что любое свободно падающее тело, будучи бро­шенным в некотором направлении, движется по параболе.