
|  поддержка курсаОсновы дискретной математики поддержка курсаОсновы дискретной математики
информация [+]Автор: М.И. Дехтярь
Студентам: электронная книга | литература | указатель | учебники | форум | мнения | однокурсники| рейтинг
экзамен
экстернат
диплом
Лекции:
· 1
· 2
· 3
· 4
· 5
· 6
· 7
· 8
· 9
· 10
· 11

| | 1. Лекция: Предварительные сведения
| | Страницы: 1 | 2 | 3 | вопросы | »
| для печати и PDA
| 
| | Если Вы заметили ошибку - сообщите нам или выделите ее и нажмите Ctrl+Enter
| | | 
| Множества и операции над ними. Как доказывать равенство множеств? Отношения и функции. Отношения эквивалентности и частичного порядка. Мощность множеств
Содержание
- Множества
- Операции над множествами
- Как доказывать равенство множеств?
- Отношения и функции. Мощность множества
Множества
Множество - это одно из основных понятий математики, как дискретной, так и непрерывной. Оно не определяется через другие понятия. Содержательно, подмножеством понимается некоторая совокупность элементов. Основное отношение между элементами и множеством - этоотношение принадлежности элемента множеству. Оно обозначается знаком 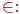  означает, что элемент xпринадлежит множеству A. означает, что элемент xпринадлежит множеству A. 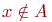 означает, что элемент x не входит в множество A. означает, что элемент x не входит в множество A. 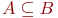 означает, что каждый элементмножества A является также элементом множества B. В этом случае множество A называется подмножеством множества B. Если означает, что каждый элементмножества A является также элементом множества B. В этом случае множество A называется подмножеством множества B. Если 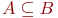 и и 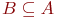 , то A=B, т.е. множества A и B равны. Если , то A=B, т.е. множества A и B равны. Если 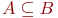 и и 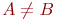 , то A называется собственнымподмножеством множества B, и в этом случае пишем , то A называется собственнымподмножеством множества B, и в этом случае пишем  .Множество, не содержащее элементов, называется пустым и обозначается .Множество, не содержащее элементов, называется пустым и обозначается  .
Обычно множества обозначаются с помощью пары фигурных скобок, в которые заключены их элементы. Небольшие множества задаются прямым перечислением всех элементов. Например, множество простых чисел, не превосходящих 10, это {2, 3, 5, 7} ; множество (имен) летних месяцев: {июнь, июль, август}. В описаниях "больших" конечных множеств используют многоточие. В них часто указывается несколько первых элементов и последний элемент множества. Например, множество целых неотрицательных чисел, не превосходящих 100, записывают как {0, 1, 2, ... , 100}, множествовсех месяцев года - как { январь, февраль, ..., декабрь}. Такое задание требует определенной аккуратности. Например, если некоторое множество A задано как {3, 5, 7, ... , 19}, то не ясно, является ли A множеством нечетных чисел, лежащих в интервале от 3 до 19, или это множествопростых чисел из того же интервала (возможны и другие его расшифровки). Перечисления элементов бесконечных множеств начинаются несколькими начальными элементами, а завершаются многоточием. При этом часто указывают общий вид элемента задаваемого множества. Основное бесконечноемножество, рассматриваемое в дискретной математике, это множество всех натуральных чисел N={0, 1, 2, 3, ... } . Множество всех квадратов этих чисел можно задать, например, так: {0, 1, 4, 9, ..., n2, ... } .
Как мы уже отметили, большие множества не всегда можно точно определить, используя перечисление с многоточием. Основной способ их описания имеет вид: { Elem | условие на Elem}, где Elem - это общий вид элемента определяемого множества, а после вертикальной черты описано условие, которому этот элемент должен удовлетворять. Например, .
Обычно множества обозначаются с помощью пары фигурных скобок, в которые заключены их элементы. Небольшие множества задаются прямым перечислением всех элементов. Например, множество простых чисел, не превосходящих 10, это {2, 3, 5, 7} ; множество (имен) летних месяцев: {июнь, июль, август}. В описаниях "больших" конечных множеств используют многоточие. В них часто указывается несколько первых элементов и последний элемент множества. Например, множество целых неотрицательных чисел, не превосходящих 100, записывают как {0, 1, 2, ... , 100}, множествовсех месяцев года - как { январь, февраль, ..., декабрь}. Такое задание требует определенной аккуратности. Например, если некоторое множество A задано как {3, 5, 7, ... , 19}, то не ясно, является ли A множеством нечетных чисел, лежащих в интервале от 3 до 19, или это множествопростых чисел из того же интервала (возможны и другие его расшифровки). Перечисления элементов бесконечных множеств начинаются несколькими начальными элементами, а завершаются многоточием. При этом часто указывают общий вид элемента задаваемого множества. Основное бесконечноемножество, рассматриваемое в дискретной математике, это множество всех натуральных чисел N={0, 1, 2, 3, ... } . Множество всех квадратов этих чисел можно задать, например, так: {0, 1, 4, 9, ..., n2, ... } .
Как мы уже отметили, большие множества не всегда можно точно определить, используя перечисление с многоточием. Основной способ их описания имеет вид: { Elem | условие на Elem}, где Elem - это общий вид элемента определяемого множества, а после вертикальной черты описано условие, которому этот элемент должен удовлетворять. Например, 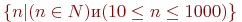 - этомножество целых чисел в интервале от 10 до 1000, - этомножество целых чисел в интервале от 10 до 1000, 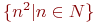 - множество квадратов натуральных чисел, - множество квадратов натуральных чисел, 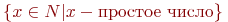 - множество всех простых чисел.
Множества, элементами которых являются другие множества, часто называют семействами или классами. Семейство ( множество ) всех подмножеств множества A обозначается через 2A, т.е. - множество всех простых чисел.
Множества, элементами которых являются другие множества, часто называют семействами или классами. Семейство ( множество ) всех подмножеств множества A обозначается через 2A, т.е. 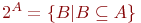 . Например, если A={ 0, 1, {2,3}}, то . Например, если A={ 0, 1, {2,3}}, то 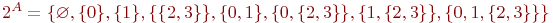 , а для пустого множества , а для пустого множества  семейство его подмножеств семейство его подмножеств 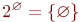 .
Операции над множествами
Имеется целый ряд операций, позволяющих получать одни множества из других. Рассмотрим основные из них.
Объединениеммножеств A и B называется множество .
Операции над множествами
Имеется целый ряд операций, позволяющих получать одни множества из других. Рассмотрим основные из них.
Объединениеммножеств A и B называется множество
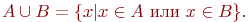 Объединением семейства множеств
Объединением семейства множеств 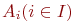 называется множество называется множество
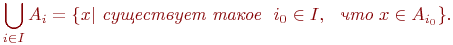 Пересечениеммножеств A и B называется множество
Пересечениеммножеств A и B называется множество
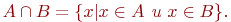 Пересечением семейства множеств
Пересечением семейства множеств 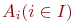 называется множество называется множество
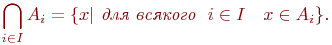 Из определения операций объединения и пересечения непосредственно следует, что они обладают свойствами ассоциативности:
Из определения операций объединения и пересечения непосредственно следует, что они обладают свойствами ассоциативности: 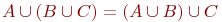 , , 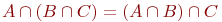 и коммутативности и коммутативности 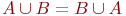 , , 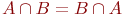 .
Разностьюмножеств A и B называется множество .
Разностьюмножеств A и B называется множество
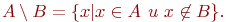 Обычно все рассматриваемые множества являются подмножествами некоторого "универсального"множества U. Разность U \ A называется дополнением множества A (в U ) и обозначается через
Обычно все рассматриваемые множества являются подмножествами некоторого "универсального"множества U. Разность U \ A называется дополнением множества A (в U ) и обозначается через 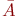 . Ясно, что . Ясно, что 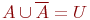 и и 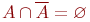 .
Симметрической разностью множеств A и B называется множество .
Симметрической разностью множеств A и B называется множество
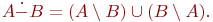 Иногда симметрическую разность множеств называют дизъюнктивной суммой и обозначают
Иногда симметрическую разность множеств называют дизъюнктивной суммой и обозначают  или или  .
Декартовым (прямым) произведениеммножеств A1, ... , An называется множество n -ок .
Декартовым (прямым) произведениеммножеств A1, ... , An называется множество n -ок
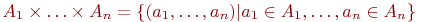 .
Если A1= ... =An=A, то A1 x ... An называется декартовой (прямой) степеньюмножества A и обозначается через An .
.
Если A1= ... =An=A, то A1 x ... An называется декартовой (прямой) степеньюмножества A и обозначается через An .
| |
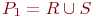 , содержащее все кортежи отношения R и все кортежи отношения S (кортежи, содержащиеся и в R, и в S, входят в P в одном экземпляре). Это отношение представляется формулой
, содержащее все кортежи отношения R и все кортежи отношения S (кортежи, содержащиеся и в R, и в S, входят в P в одном экземпляре). Это отношение представляется формулой 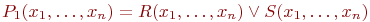 . Результат пересечения - это отношение P2 = R \cap S, которое содержит кортежи, входящие и в R и в S. Оно представляется формулой
. Результат пересечения - это отношение P2 = R \cap S, которое содержит кортежи, входящие и в R и в S. Оно представляется формулой 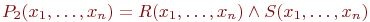 . Результат разности P3= R - S включает кортежи из R, не входящие в S. Это отношение представляется формулой
. Результат разности P3= R - S включает кортежи из R, не входящие в S. Это отношение представляется формулой  . Декартово произведение P4= R x S отношенийR(A1, ..., An) и S(B1, ..., Bm) содержит кортежи, которые составлены из кортежей отношения R, продолженных кортежами отношения S. Список атрибутов P4 включает все атрибуты отношений R и S: (A1, ..., An, B1, ..., Bm). Если у R и S имеются общие атрибуты, то они переименовываются. Обычно перед именем атрибута общего атрибута Ai=Bj помещается через точку имя его отношения,R.Ai и S.Bj. Результат декартового произведения задается формулой
. Декартово произведение P4= R x S отношенийR(A1, ..., An) и S(B1, ..., Bm) содержит кортежи, которые составлены из кортежей отношения R, продолженных кортежами отношения S. Список атрибутов P4 включает все атрибуты отношений R и S: (A1, ..., An, B1, ..., Bm). Если у R и S имеются общие атрибуты, то они переименовываются. Обычно перед именем атрибута общего атрибута Ai=Bj помещается через точку имя его отношения,R.Ai и S.Bj. Результат декартового произведения задается формулой 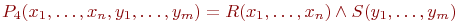 (мы предполагаем, что все переменные xi и yj разные).
(мы предполагаем, что все переменные xi и yj разные).

 поддержка курсаОсновы дискретной математики
поддержка курсаОсновы дискретной математики 
 означает, что элемент xпринадлежит множеству A.
означает, что элемент xпринадлежит множеству A. 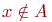 означает, что элемент x не входит в множество A.
означает, что элемент x не входит в множество A. 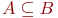 означает, что каждый элементмножества A является также элементом множества B. В этом случае множество A называется подмножеством множества B. Если
означает, что каждый элементмножества A является также элементом множества B. В этом случае множество A называется подмножеством множества B. Если 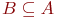 , то A=B, т.е. множества A и B равны. Если
, то A=B, т.е. множества A и B равны. Если 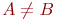 , то A называется собственнымподмножеством множества B, и в этом случае пишем
, то A называется собственнымподмножеством множества B, и в этом случае пишем  .Множество, не содержащее элементов, называется пустым и обозначается
.Множество, не содержащее элементов, называется пустым и обозначается  .
Обычно множества обозначаются с помощью пары фигурных скобок, в которые заключены их элементы. Небольшие множества задаются прямым перечислением всех элементов. Например, множество простых чисел, не превосходящих 10, это {2, 3, 5, 7} ; множество (имен) летних месяцев: {июнь, июль, август}. В описаниях "больших" конечных множеств используют многоточие. В них часто указывается несколько первых элементов и последний элемент множества. Например, множество целых неотрицательных чисел, не превосходящих 100, записывают как {0, 1, 2, ... , 100}, множествовсех месяцев года - как { январь, февраль, ..., декабрь}. Такое задание требует определенной аккуратности. Например, если некоторое множество A задано как {3, 5, 7, ... , 19}, то не ясно, является ли A множеством нечетных чисел, лежащих в интервале от 3 до 19, или это множествопростых чисел из того же интервала (возможны и другие его расшифровки). Перечисления элементов бесконечных множеств начинаются несколькими начальными элементами, а завершаются многоточием. При этом часто указывают общий вид элемента задаваемого множества. Основное бесконечноемножество, рассматриваемое в дискретной математике, это множество всех натуральных чисел N={0, 1, 2, 3, ... } . Множество всех квадратов этих чисел можно задать, например, так: {0, 1, 4, 9, ..., n2, ... } .
Как мы уже отметили, большие множества не всегда можно точно определить, используя перечисление с многоточием. Основной способ их описания имеет вид: { Elem | условие на Elem}, где Elem - это общий вид элемента определяемого множества, а после вертикальной черты описано условие, которому этот элемент должен удовлетворять. Например,
.
Обычно множества обозначаются с помощью пары фигурных скобок, в которые заключены их элементы. Небольшие множества задаются прямым перечислением всех элементов. Например, множество простых чисел, не превосходящих 10, это {2, 3, 5, 7} ; множество (имен) летних месяцев: {июнь, июль, август}. В описаниях "больших" конечных множеств используют многоточие. В них часто указывается несколько первых элементов и последний элемент множества. Например, множество целых неотрицательных чисел, не превосходящих 100, записывают как {0, 1, 2, ... , 100}, множествовсех месяцев года - как { январь, февраль, ..., декабрь}. Такое задание требует определенной аккуратности. Например, если некоторое множество A задано как {3, 5, 7, ... , 19}, то не ясно, является ли A множеством нечетных чисел, лежащих в интервале от 3 до 19, или это множествопростых чисел из того же интервала (возможны и другие его расшифровки). Перечисления элементов бесконечных множеств начинаются несколькими начальными элементами, а завершаются многоточием. При этом часто указывают общий вид элемента задаваемого множества. Основное бесконечноемножество, рассматриваемое в дискретной математике, это множество всех натуральных чисел N={0, 1, 2, 3, ... } . Множество всех квадратов этих чисел можно задать, например, так: {0, 1, 4, 9, ..., n2, ... } .
Как мы уже отметили, большие множества не всегда можно точно определить, используя перечисление с многоточием. Основной способ их описания имеет вид: { Elem | условие на Elem}, где Elem - это общий вид элемента определяемого множества, а после вертикальной черты описано условие, которому этот элемент должен удовлетворять. Например, 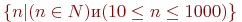 - этомножество целых чисел в интервале от 10 до 1000,
- этомножество целых чисел в интервале от 10 до 1000, 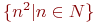 - множество квадратов натуральных чисел,
- множество квадратов натуральных чисел, 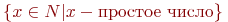 - множество всех простых чисел.
Множества, элементами которых являются другие множества, часто называют семействами или классами. Семейство ( множество ) всех подмножеств множества A обозначается через 2A, т.е.
- множество всех простых чисел.
Множества, элементами которых являются другие множества, часто называют семействами или классами. Семейство ( множество ) всех подмножеств множества A обозначается через 2A, т.е. 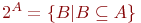 . Например, если A={ 0, 1, {2,3}}, то
. Например, если A={ 0, 1, {2,3}}, то 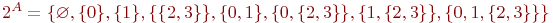 , а для пустого множества
, а для пустого множества 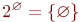 .
Операции над множествами
Имеется целый ряд операций, позволяющих получать одни множества из других. Рассмотрим основные из них.
Объединениеммножеств A и B называется множество
.
Операции над множествами
Имеется целый ряд операций, позволяющих получать одни множества из других. Рассмотрим основные из них.
Объединениеммножеств A и B называется множество
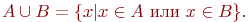 Объединением семейства множеств
Объединением семейства множеств 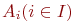 называется множество
называется множество
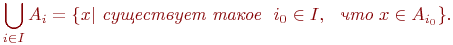 Пересечениеммножеств A и B называется множество
Пересечениеммножеств A и B называется множество
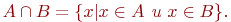 Пересечением семейства множеств
Пересечением семейства множеств 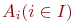 называется множество
называется множество
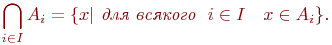 Из определения операций объединения и пересечения непосредственно следует, что они обладают свойствами ассоциативности:
Из определения операций объединения и пересечения непосредственно следует, что они обладают свойствами ассоциативности: 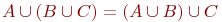 ,
, 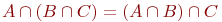 и коммутативности
и коммутативности 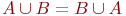 ,
, 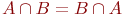 .
Разностьюмножеств A и B называется множество
.
Разностьюмножеств A и B называется множество
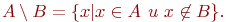 Обычно все рассматриваемые множества являются подмножествами некоторого "универсального"множества U. Разность U \ A называется дополнением множества A (в U ) и обозначается через
Обычно все рассматриваемые множества являются подмножествами некоторого "универсального"множества U. Разность U \ A называется дополнением множества A (в U ) и обозначается через 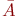 . Ясно, что
. Ясно, что 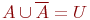 и
и 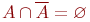 .
Симметрической разностью множеств A и B называется множество
.
Симметрической разностью множеств A и B называется множество
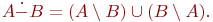 Иногда симметрическую разность множеств называют дизъюнктивной суммой и обозначают
Иногда симметрическую разность множеств называют дизъюнктивной суммой и обозначают  или
или  .
Декартовым (прямым) произведениеммножеств A1, ... , An называется множество n -ок
.
Декартовым (прямым) произведениеммножеств A1, ... , An называется множество n -ок
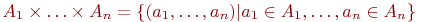 .
Если A1= ... =An=A, то A1 x ... An называется декартовой (прямой) степеньюмножества A и обозначается через An .
.
Если A1= ... =An=A, то A1 x ... An называется декартовой (прямой) степеньюмножества A и обозначается через An .









