Семантика: системы и значения формул на их состояниях
Даже приведенных выше небольших примеров достаточно, чтобы понять, что семантика (т.е. значение, смысл) формул логики предикатов зависит от состояния дел в той предметной области, о которой идет речь в формулах, и от значений их свободных переменных. Для того, чтобы ее определить, нужно уточнить, свойства какой предметной области мы собираемся описывать с помощью формул и как в этой области интерпретируются символы предикатов, функций и констант нашего языка.
Определение 7.4. Алгебраической системой или просто системой1). Сигнатуры 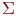 называется непустое множество Aвместе с отображением, которое каждому n -местному предикатному (функциональному) символу из
называется непустое множество Aвместе с отображением, которое каждому n -местному предикатному (функциональному) символу из 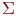 сопоставляет n-местный предикат ( n -местную функцию) на
сопоставляет n-местный предикат ( n -местную функцию) на 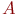 , а каждой константе из
, а каждой константе из 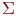 - некоторый элемент из A. A называется основным множеством системы. Если множество F имен функций в
- некоторый элемент из A. A называется основным множеством системы. Если множество F имен функций в 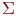 пусто, то соответствующую систему часто называют моделью.
пусто, то соответствующую систему часто называют моделью.
Определенную таким образом систему будем обозначать как 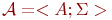 , используя для предикатов и функций системы их имена из сигнатуры
, используя для предикатов и функций системы их имена из сигнатуры 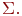
Определим теперь интерпретации свободных переменных.
Определение 7.5. Состоянием (оценкой) системы 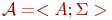 назывется отображение
назывется отображение 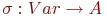 , которое каждой переменной
, которое каждой переменной 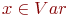 сопоставляет ее значение в данном состоянии
сопоставляет ее значение в данном состоянии 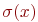 .
.
Имея систему и состояние, можно говорить о значениях термов и формул на данном состоянии системы. Мы будем считать, что в определениях ниже зафиксирована некоторая система 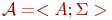 , будем через
, будем через 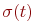 и
и 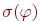 обозначать значение терма t и формулы
обозначать значение терма t и формулы 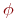 на состоянии
на состоянии  системы
системы 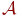 . И то, и другое определяется индукцией по построению термов и формул соответственно.
. И то, и другое определяется индукцией по построению термов и формул соответственно.
Определение 7.6. Значение терма.
- Для переменной
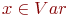
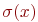 уже определено в состоянии
уже определено в состоянии 
- Если t является константой
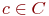 , то
, то 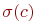 не зависит от
не зависит от  и равно значению этой константы при данной интерпретации
и равно значению этой константы при данной интерпретации - (напомним, в интерпретации каждой константе сопоставлен некоторый элемент основного множества).
- Если t имеет вид f(t1,...,tm), где
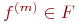 - символ m - местной функции, а t1,...,tm -термы, то
- символ m - местной функции, а t1,...,tm -термы, то 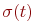 есть
есть  , где fA есть функция, соответствующая символу f в системе
, где fA есть функция, соответствующая символу f в системе 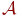 .
.
Таким образом, чтобы определить значение терма на состоянии, нужно подставить в него задаваемые этим состоянием значения переменных и вычислить значение получившейся суперпозиции функций на основном множестве системы.
Определение 7.7. Значение атомной формулы.
- Если
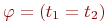 , где t1 и t2 - термы, то
, где t1 и t2 - термы, то 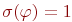 , если
, если 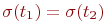 , и
, и 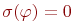 , если
, если 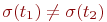 .
. - Пусть
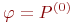 - 0 -местный предикатный символ из P и PA - это 0 -местный предикат, сопоставленный ему в
- 0 -местный предикатный символ из P и PA - это 0 -местный предикат, сопоставленный ему в 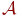 . Тогда
. Тогда 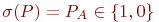 .
.
· Пусть 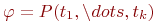 , где P(k) - предикатный k -местный символ из P, t1,...,tk - термы, аPA - это k -местный предикат, сопоставленный P(k) в
, где P(k) - предикатный k -местный символ из P, t1,...,tk - термы, аPA - это k -местный предикат, сопоставленный P(k) в 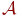 . Тогда
. Тогда
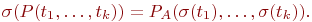
Таким образом, равенство термов на некотором состоянии истинно, если эти термы имеют на этомсостоянии одинаковые значения. Для определения истинности предиката от набора термов нужно вычислить их значения на заданном состоянии и проверить, входит ли получившийся набор значений во множество наборов, принадлежащих данному предикату.
Определение 7.8. Значение формулы.
Если 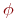 - атомная формула, то ее значение
- атомная формула, то ее значение 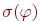 определено выше. Значения сложных формулопределяются следующим образом.
определено выше. Значения сложных формулопределяются следующим образом.
- Если
 , то
, то 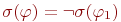 .
. - Если
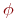 имеет одну из форм
имеет одну из форм 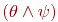 ,
, 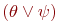 или
или 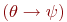 , то значение
, то значение 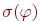
- равно значению
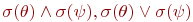 или
или 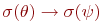 , соответственно.
, соответственно. - Если
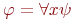 , то
, то 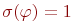 , если
, если 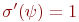 для
для 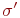 , которое может отличаться от
, которое может отличаться от  только значением переменной x, т.е. такого
только значением переменной x, т.е. такого 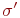 , что
, что 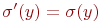 при
при 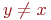 , иначе
, иначе 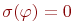 .
. - Если
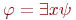 , то
, то 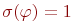 , если существует такое состояние
, если существует такое состояние 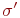 , которое может отличаться от
, которое может отличаться от  только значением переменной x, для которого
только значением переменной x, для которого 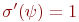 , иначе
, иначе 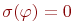 .
.
Прокомментируем два последних пункта. Для истинности формулы вида 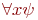 (она читается: "для всехx имеет место (выполняется, истинно, справедливо)
(она читается: "для всехx имеет место (выполняется, истинно, справедливо) 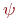 ") на состоянии
") на состоянии  нужно убедиться в том, что формула
нужно убедиться в том, что формула 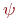 истинна при замене x любым элементом
истинна при замене x любым элементом  , т.е. на любом состоян ии, получающемся из
, т.е. на любом состоян ии, получающемся из  изменением значения на переменной x:
изменением значения на переменной x: 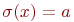 . Для истинности формулы вида
. Для истинности формулы вида 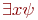 (она читается: "существует такое x, что имеет место (выполняется, истинно, справедливо)
(она читается: "существует такое x, что имеет место (выполняется, истинно, справедливо) 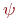 ") насостоянии
") насостоянии  достаточно найти такое значение
достаточно найти такое значение  , что при подстановке a вместо x в формулу
, что при подстановке a вместо x в формулу 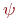 она будет истинна при неизменившихся значениях остальных свободных переменных.
она будет истинна при неизменившихся значениях остальных свободных переменных.
Из приведенных определений нетрудно вывести, что значение формулы на некотором состояниизависит лишь от значений ее свободных переменных в этом состоянии.
Предложение 7.1. Пусть 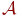 - система сигнатуры
- система сигнатуры 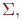
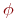 - формула той же сигнатуры,
- формула той же сигнатуры, 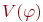 - множество ее свободных переменных. Тогда для любых двух состояний
- множество ее свободных переменных. Тогда для любых двух состояний 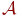
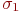 и
и 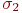 , совпадающих на
, совпадающих на 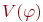 (т.е. таких, что для всякой
(т.е. таких, что для всякой 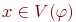
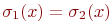 ), имеет место равенство
), имеет место равенство 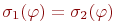 .
.
Доказательство получается индукцией по построению формулы 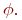 Действительно, утверждение, очевидно, справедливо для значений термов и атомных формул. Из предположения о его справедливости для формул
Действительно, утверждение, очевидно, справедливо для значений термов и атомных формул. Из предположения о его справедливости для формул 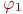 и
и 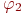 его легко перенести на формулы вида
его легко перенести на формулы вида 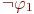 и
и 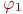

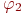 , где
, где 
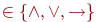 . ( Проведите это рассуждение самостоятельно!). Пусть теперь
. ( Проведите это рассуждение самостоятельно!). Пусть теперь 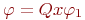 , где
, где 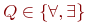 , а
, а 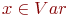 . Тогда
. Тогда 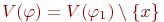 . Пусть
. Пусть 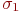 и
и 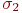 - состояния, совпадающие на
- состояния, совпадающие на 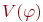 . Рассмотрим множества состояний, отличающихся от них только на x:
. Рассмотрим множества состояний, отличающихся от них только на x: 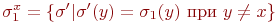 и
и 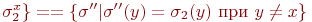 . Для каждого состояния
. Для каждого состояния 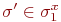 в
в 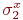 имеется состояние
имеется состояние 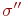 , совпадающее с
, совпадающее с 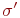 на
на 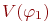 . Верно и обратное. Поэтому по предположению индукции в
. Верно и обратное. Поэтому по предположению индукции в 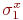 имеется состояние
имеется состояние 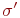 , для которого
, для которого 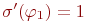 тогда и только тогда, когда в
тогда и только тогда, когда в 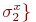 имеется состояние
имеется состояние 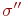 , для которого
, для которого 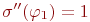 . Отсюда и из определения значения формулы
. Отсюда и из определения значения формулы 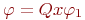 следует, что
следует, что 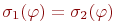 .
.
Из этого предложения немедленно вытекает
Следствие. Значение замкнутой формулы не зависит от состояния, на котором она оценивается, т.е. либо на всех состояниях системы она истинна, либо на всех состояниях системы эта формула ложна.
Определение 7.9. Формула 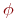 называется истинной на системе
называется истинной на системе 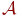 , если для любого состояния
, если для любого состояния  этой системы
этой системы 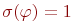 . В этом случае пишем
. В этом случае пишем 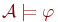 .
.
Формула 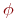 называется тождественно истинной (общезначимой), если она истинна на всехалгебраических системах своей сигнатуры. В этом случае пишем
называется тождественно истинной (общезначимой), если она истинна на всехалгебраических системах своей сигнатуры. В этом случае пишем 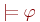 . Тождественно истинные формулы называют также законами логики.
. Тождественно истинные формулы называют также законами логики.
Пример 7.4. В качестве примера рассмотрим следующую систему 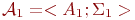 для определенной выше примере 7.2 сигнатуры
для определенной выше примере 7.2 сигнатуры 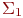 .
.
Ее основное множество A1 включает множество натуральных чисел N={0, 1, 2, ... }, для которых истинен предикат число и множество людей { петр, джон, ольга, иван, мария }, для которых истинен предикат человек (мы используем для объектов-людей имена, начинающиеся со строчных букв, чтобы отличить их от имен констант из сигнатуры). Пусть, кроме того, A1 включает специальный объект  соответствующий неопределенному (или ошибочному) значению. Константы интерпретируются естественным образом: числовые - соответствующими числами, имена людей - людьми с теми же именами.
соответствующий неопределенному (или ошибочному) значению. Константы интерпретируются естественным образом: числовые - соответствующими числами, имена людей - людьми с теми же именами.
| x | отец(x) | лучший_друг(x) | зарплата(x) |
| петр | иван | джон | |
| джон | петр | ольга | |
| ольга | джон | петр | |
| иван | 
| мария | |
| мария | иван | петр |
Функция + на числах интерпретируется обычным сложением, а в остальных случаях ее значением является  Интерпретации остальных функций заданы в таблице (для числовых аргументов все они равны
Интерпретации остальных функций заданы в таблице (для числовых аргументов все они равны  ). Предикат
). Предикат  интерпретируется обычным образом на числах и ложен, если хоть один его аргумент не число ( мы будем для него использовать стандартную форму записи x <= y вместо <=(x,y)). Остальные предикаты зададим перечислением пар, на которых они истинны:
интерпретируется обычным образом на числах и ложен, если хоть один его аргумент не число ( мы будем для него использовать стандартную форму записи x <= y вместо <=(x,y)). Остальные предикаты зададим перечислением пар, на которых они истинны:
живут_рядом = { (ольга,петр), (петр, ольга), (иван, джон), (джон, иван), (мария, ольга), (ольга, мария) }
родственники = { (ольга,петр), (петр, ольга), (джон, петр), (петр, джон), (ольга, джон), (джон, ольга), (иван, мария), (мария, иван) }.
Пусть множество переменных Var= {x, y, z, i, n, k, ...} и состояние  определяет их значения следующим образом:
определяет их значения следующим образом:
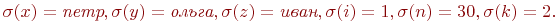
Определим значения некоторых термов на 
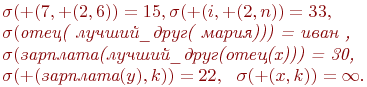
Рассмотрим теперь введенные выше формулы

и
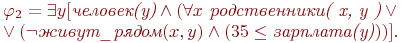
Чтобы оценить первую из них на состоянии  мы должны проверить ее подформулу
мы должны проверить ее подформулу 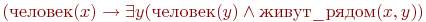 на всех состояниях
на всех состояниях 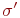 , совпадающих с
, совпадающих с  на всех переменных кроме, быть может, x. Если
на всех переменных кроме, быть может, x. Если 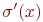 - число или
- число или  то
то  , а вся импликация = 1. Если же
, а вся импликация = 1. Если же 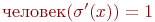 , т. е
, т. е 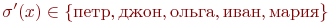 , то легко проверить, что для каждого из этих значений x найдется такое значение
, то легко проверить, что для каждого из этих значений x найдется такое значение 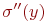 , для которого выполнено
, для которого выполнено 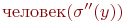 , и что имеет место
, и что имеет место 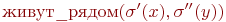 . Например, если
. Например, если 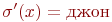 , то в качестве
, то в качестве 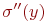 следует взять иван. Таким образом формула
следует взять иван. Таким образом формула 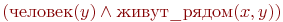 будет иметь значение 1 на состоянии
будет иметь значение 1 на состоянии 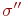 , совпадающем с
, совпадающем с 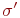 на всех переменных кроме, быть может, y. Следовательно, мы показали, что
на всех переменных кроме, быть может, y. Следовательно, мы показали, что 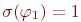 . Заметим, что так как
. Заметим, что так как 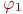 - замкнутая формула, то на самом деле, мы показали, что она имеет значение 1 на любомсостоянии системы
- замкнутая формула, то на самом деле, мы показали, что она имеет значение 1 на любомсостоянии системы 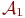 , т.е. что
, т.е. что 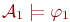 .
.
Для оценки значения 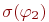 нужно постараться найти такого человека
нужно постараться найти такого человека 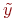 , для которого выполняется хотя бы одна из подформул
, для которого выполняется хотя бы одна из подформул  или
или 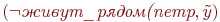
 (напомним, что
(напомним, что 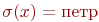 ). Из определения предиката родственники в
). Из определения предиката родственники в  следует, что первая из этих формул не выполняется ни для какого
следует, что первая из этих формул не выполняется ни для какого 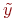 . Что касается второй подформулы, то она верна при
. Что касается второй подформулы, то она верна при 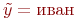 или
или 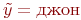 , поскольку оба они не являются соседямипетр а и имеют зарплату >= 35. Таким образом,
, поскольку оба они не являются соседямипетр а и имеют зарплату >= 35. Таким образом, 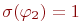 .
.
Эквивалентные формулы и нормальные формы
С понятием эквивалентности формул мы уже знакомились, когда рассматривали булевы формулы (формулы логики высказываний). Для логики предикатов эквивалентность определяется следующим образом.
Определение 7.10. Формулы 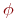 и и 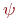 сигнатуры сигнатуры 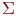 называются эквивалентными, если для любой системы называются эквивалентными, если для любой системы  этой сигнатуры и любого ее состояния этой сигнатуры и любого ее состояния  имеет место равенство имеет место равенство 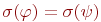 . В этом случае пишем . В этом случае пишем  .
Отметим сначала, что все эквивалентности булевых формул, приведенные в лекции 4: законы ассоциативности и коммутативности для конъюнкции и дизъюнкции, законы дистрибутивности, двойного отрицания, де Моргана и др., остаются справедливыми и для формул логики предикатов. Поэтому и для них мы примем соглашение об упрощенной записи, которое позволяет опускать скобки в формулах, содержащих только операции конъюнкции или только операции дизъюнкции. Разрешим также опускать внешние скобки в формулах, внешняя функция которых .
Отметим сначала, что все эквивалентности булевых формул, приведенные в лекции 4: законы ассоциативности и коммутативности для конъюнкции и дизъюнкции, законы дистрибутивности, двойного отрицания, де Моргана и др., остаются справедливыми и для формул логики предикатов. Поэтому и для них мы примем соглашение об упрощенной записи, которое позволяет опускать скобки в формулах, содержащих только операции конъюнкции или только операции дизъюнкции. Разрешим также опускать внешние скобки в формулах, внешняя функция которых 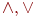 или или  Например, формула Например, формула 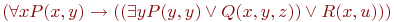 может быть упрощенно записана как может быть упрощенно записана как 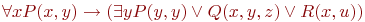 .
Для логики предикатов остается справедливым и правило замены эквивалентных подформул:
если .
Для логики предикатов остается справедливым и правило замены эквивалентных подформул:
если 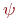 является подформулой формулы является подформулой формулы 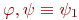 и формула и формула 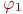 получена из формулы получена из формулы 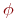 заменой некоторого вхождения заменой некоторого вхождения 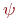 на на 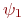 , то , то  .
Доказательство этого правила получается индукцией по определению значения формулы на состоянии системы (см. задачу 7.8).
Новые эквивалентности связаны с кванторами.
Теорема 7.1. Для любых формул .
Доказательство этого правила получается индукцией по определению значения формулы на состоянии системы (см. задачу 7.8).
Новые эквивалентности связаны с кванторами.
Теорема 7.1. Для любых формул 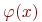 и и 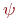 таких, что таких, что 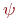 не содержит свободно переменной x, имеют место следующие эквивалентности. не содержит свободно переменной x, имеют место следующие эквивалентности.
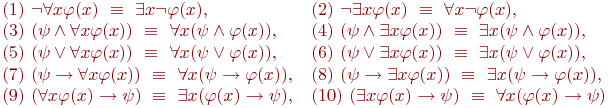 Доказательствавсех этих эквивалентностей получаются непосредственно из определения значения формул на состояниях. Рассмотрим, например, первую из них. Для любого состояния
Доказательствавсех этих эквивалентностей получаются непосредственно из определения значения формул на состояниях. Рассмотрим, например, первую из них. Для любого состояния  имеем имеем  . Это значение равно 1 тогда и только тогда, когда . Это значение равно 1 тогда и только тогда, когда 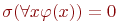 или, по определению значения квантора или, по определению значения квантора 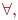 когда найдется такое состояние когда найдется такое состояние 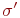 , совпадающее с , совпадающее с  внеx, для которого внеx, для которого 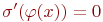 . Но это эквивалентно истинности формулы . Но это эквивалентно истинности формулы 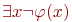 на состоянии на состоянии  Рассмотрим еще эквивалентности (9) и (10), которые, на первый взгляд, могут удивить - квантор всеобщности превращается при вынесении за скобки в квантор существования и наоборот. Доказательство (9) получается с помощью булевых эквивалентностей и пунктов (1) и (4) настоящей теоремы:
Рассмотрим еще эквивалентности (9) и (10), которые, на первый взгляд, могут удивить - квантор всеобщности превращается при вынесении за скобки в квантор существования и наоборот. Доказательство (9) получается с помощью булевых эквивалентностей и пунктов (1) и (4) настоящей теоремы:
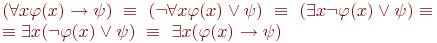 Эквивалентность (10) доказывается аналогично.
Останутся ли эквивалентности (2) - (8) справедливыми, если мы не будем требовать, чтобы формула
Эквивалентность (10) доказывается аналогично.
Останутся ли эквивалентности (2) - (8) справедливыми, если мы не будем требовать, чтобы формула 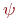 не содержала свободных вхождений переменной x? Нет! Рассмотрим, например, для арифметической сигнатуры две формулы не содержала свободных вхождений переменной x? Нет! Рассмотрим, например, для арифметической сигнатуры две формулы 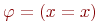 и и 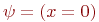 . Тогда формула . Тогда формула 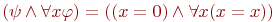 , представляющая левую часть эквивалентности (3) истинна насостоянии , представляющая левую часть эквивалентности (3) истинна насостоянии  в котором $ в котором $  (x)=0.$ А формула (x)=0.$ А формула 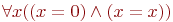 , представляющая ее правую часть, ложна на всех состояниях. Чтобы корректно вынести за скобки квантор в формуле , представляющая ее правую часть, ложна на всех состояниях. Чтобы корректно вынести за скобки квантор в формуле 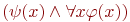 , в которой , в которой 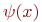 содержит x свободно, нужно предварительно переименоватьсвязанную переменную в содержит x свободно, нужно предварительно переименоватьсвязанную переменную в 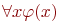 . Это позволяют сделать следующие эквивалентности, справедливость которых следует из предложения 7.1.
Лемма 7.1.О замене связанных переменных. . Это позволяют сделать следующие эквивалентности, справедливость которых следует из предложения 7.1.
Лемма 7.1.О замене связанных переменных.
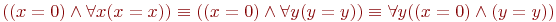 . В общем случае, если переменная y не входит в . В общем случае, если переменная y не входит в 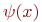 и в и в 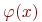 , справедлива эквивалентность , справедлива эквивалентность  .
Определение 7.11. Формула вида .
Определение 7.11. Формула вида 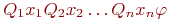 , где , где 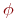 - бескванторная формула, а каждый символ Qi - это один из кванторов - бескванторная формула, а каждый символ Qi - это один из кванторов  или или 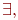 называется предваренной (или пренексной)нормальной формой. Последовательность кванторов Q1 x1 Q2 x2 ... Qn xn называется ее приставкой, а бескванторная формула называется предваренной (или пренексной)нормальной формой. Последовательность кванторов Q1 x1 Q2 x2 ... Qn xn называется ее приставкой, а бескванторная формула 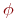 - матрицей этой нормальной формы.
Теорема 7.2. О предваренной форме.
Для всякой формулы - матрицей этой нормальной формы.
Теорема 7.2. О предваренной форме.
Для всякой формулы 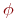 существует формула существует формула 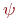 в предваренной нормальной форме такая, что в предваренной нормальной форме такая, что  .
Доказательство следует из теоремы 7.1 и леммы 7.1. Мы приведем его в виде процедуры, которая позволяет построить предваренную форму .
Доказательство следует из теоремы 7.1 и леммы 7.1. Мы приведем его в виде процедуры, которая позволяет построить предваренную форму 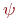 по исходной формуле по исходной формуле 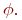 Процедура состоит из двух этапов. На первом этапе, используя лемму 7.1, заменим все связанные переменные в Процедура состоит из двух этапов. На первом этапе, используя лемму 7.1, заменим все связанные переменные в 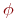 на новые так, чтобы на новые так, чтобы
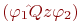 , где , где 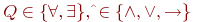 на эквивалентную формулу на эквивалентную формулу 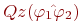 , и каждую подформулу вида , и каждую подформулу вида 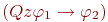 на формулу на формулу 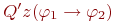 , где , где 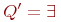 при при 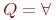 и и 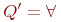 при при 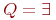 . Если после этого вынесенный квантор стоит сразу после операции отрицания . Если после этого вынесенный квантор стоит сразу после операции отрицания  то, применяя эквивалентности (1), (2), проносим отрицание в глубь формулы. Заметим, что порядок выноса кванторов определен неоднозначно, в зависимости от него в результате могут получиться эквивалентные формулы с разными кванторными приставками.
Пример 7.1. Рассмотрим пример. Пусть то, применяя эквивалентности (1), (2), проносим отрицание в глубь формулы. Заметим, что порядок выноса кванторов определен неоднозначно, в зависимости от него в результате могут получиться эквивалентные формулы с разными кванторными приставками.
Пример 7.1. Рассмотрим пример. Пусть 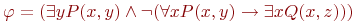 .
Ее свободные переменные: x, y и z (у x и y имеются также и связанные вхождения). Выберем в качестве новых имен для связанных переменных u, v и w и заменим ими "старые" связанные переменные. Получим эквивалентную формулу .
Ее свободные переменные: x, y и z (у x и y имеются также и связанные вхождения). Выберем в качестве новых имен для связанных переменных u, v и w и заменим ими "старые" связанные переменные. Получим эквивалентную формулу 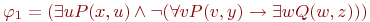 . На следующем этапе выносим кванторы за скобки (в качестве индексов у знаков эквивалентности указаны номера применяемых эквивалентностей): . На следующем этапе выносим кванторы за скобки (в качестве индексов у знаков эквивалентности указаны номера применяемых эквивалентностей):
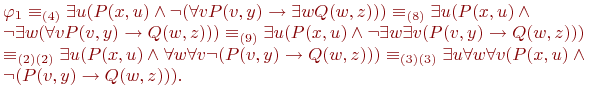 Далее можно упрощать матрицу формулы, используя известные эквивалентности булевой логики. В данном случае получим формулу
Далее можно упрощать матрицу формулы, используя известные эквивалентности булевой логики. В данном случае получим формулу
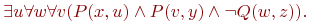
|

|
Дата добавления: 2022-05-27; просмотров: 99;

 , где
, где 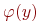 получается заменой всех свободных вхождений x в
получается заменой всех свободных вхождений x в  , где
, где 








