Правила приведения произвольной формулы алгебры логики к совершенной нормальной форме.
А. Правила приведения к СДНФ.
Из определения 8.4 следует, что формула F является СДНФ, если она отвечает следующим условиям (иначе, если она обладает следующими свойствами, называемыми “СВОЙСТВАМИ СОВЕРШЕНСТВА ”):
а) в ней нет двух одинаковых слагаемых (дизъюнктивных членов);
б) ни одно слагаемое не содержит двух одинаковых множителей;
в) никакое слагаемое не содержит переменную вместе с её отрицанием;
г) в каждом слагаемом содержится в качестве множителя либо каждая из переменных 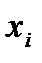 , либо её отрицание
, либо её отрицание 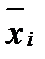 , где
, где 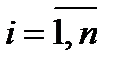 .
.
Условия а) ÷г) являются, таким образом, необходимыми и достаточными для того, чтобы ДНФ являлась СДНФ. Вместе с тем, эти условия дают возможность высказать правила, позволяющие приводить с помощью равносильных преобразований любую не тождественно ложную формулу к СДНФ, которая является для неё единственной. Итак, приведем эти правила.
Пусть дана произвольная формула F 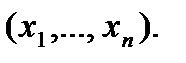
Проделаем пять операций, которые приведут формулу к СДНФ.
1) Приведем её с помощью равносильных преобразований к какой-либо ДНФ.
2) Если какое-нибудь из слагаемых этой ДНФ, например, В не содержит переменную 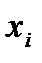 , то заменим его суммой
, то заменим его суммой 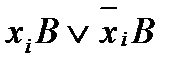 . Эта замена представляет собой равносильное преобразование, так как
. Эта замена представляет собой равносильное преобразование, так как 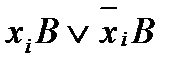
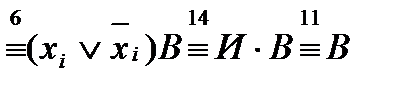 (см. также формулу расщепления R). Проделав операции по п.2), мы удовлетворили требованиям п. г) свойств совершенства.
(см. также формулу расщепления R). Проделав операции по п.2), мы удовлетворили требованиям п. г) свойств совершенства.
3) Если в полученном выражении окажутся одинаковые слагаемые, то, удалив все, кроме одного из них ( в силу закона идемпотентности (8)), мы получим опять равносильное выражение. Здесь мы удовлетворили п. а) свойств совершенства.
4) Если после этого в некоторых слагаемых окажется по несколько одинаковых множителей, то лишние (в силу закона идемпотентности (9)) удаляем. Таким образом, мы удовлетворяем п. б) свойств совершенства.
5) Наконец, удаляем все те слагаемые, которые содержат какую-нибудь переменную 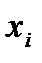 вместе со своим отрицанием
вместе со своим отрицанием 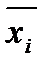 , так как, в силу закона противоречия (15), они являются тождественно ложными выражениями – удовлетворили п. в) свойств совершенства.
, так как, в силу закона противоречия (15), они являются тождественно ложными выражениями – удовлетворили п. в) свойств совершенства.
Если бы все слагаемые оказались таковыми, то и вся ДНФ была бы тождественно ложной. А тогда это значило бы, что исходная формула F – тождественно ложная формула и не имеет СДНФ. Именно поэтому мы утверждаем: если формула F не является тождественно ложной, то в её произвольной ДНФ должны присутствовать слагаемые, удовлетворяющие условию п. в) свойств совершенства.
После удаления всех слагаемых, содержащих какую-нибудь переменную вместе с её отрицанием, мы получили ДНФ, удовлетворяющую всем свойствам совершенства, т.е. СДНФ.
Заметим, что нам нет необходимости знать заранее, является ли формула F тождественно ложной или нет. Проделывая указанные операции, мы это выясним после того, как удалим все слагаемые, содержащие какую-нибудь переменную вместе с её отрицанием. Если формула F – тождественно ложная формула, то все слагаемые будут удалены, и мы не получим СДНФ.
Б. Правила приведения к СКНФ.
Из определения 8.3 следует, что СКНФ обладает следующими свойствами совершенства (иными словами, СКНФ формулы F 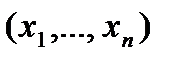 называется её КНФ, удовлетворяющая следующим условиям):
называется её КНФ, удовлетворяющая следующим условиям):
а) в ней нет двух одинаковых множителей;
б) ни один множитель не содержит двух одинаковых слагаемых;
в) ни один множитель не содержит какую-нибудь переменную 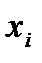 вместе с её отрицанием
вместе с её отрицанием 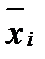 ;
;
г) каждый множитель содержит в качестве слагаемых все переменные 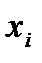 или их отрицание
или их отрицание 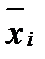 , т.е.
, т.е. 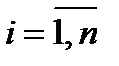 для каждого множителя.
для каждого множителя.
Можно доказать, что каждая не тождественно истинная формула имеет единственную (с точностью до порядка расположения множителей и слагаемых в множителях) СКНФ.
Правила приведения произвольной формулы к СКНФ аналогичны тем, которые описаны выше для нахождения СДНФ, и выражаются в двойственных терминах.
Пусть дана произвольная формула F 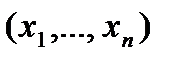 .
.
Проделаем несколько операций, которые приведут формулу к СКНФ.
1) Путем равносильных преобразований приведем формулу к КНФ.
2) Если в полученной КНФ какой-либо дизъюнктивный сомножитель В не содержит некоторую переменную 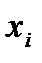 (т.е. не удовлетворяет условию совершенства п. г)), то, используя равносильность
(т.е. не удовлетворяет условию совершенства п. г)), то, используя равносильность 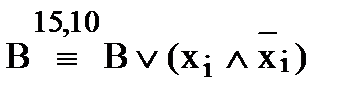 , элементарную дизъюнкцию В заменяем на две элементарных дизъюнкции:
, элементарную дизъюнкцию В заменяем на две элементарных дизъюнкции: 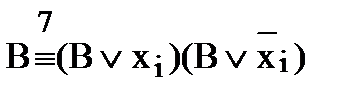 , каждая из которых уже содержит переменную
, каждая из которых уже содержит переменную 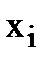 - удовлетворили условию совершенства п. г).
- удовлетворили условию совершенства п. г).
3) Если в КНФ входят две одинаковых элементарных дизъюнкции В, то лишнюю отбрасываем, поскольку 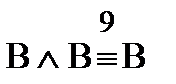 - удовлетворили условию совершенства п. а).
- удовлетворили условию совершенства п. а).
Дата добавления: 2022-05-27; просмотров: 118;










