Табличным способом.
Последовательность называется возрастающей (строго), если 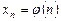 является возрастающей (строго) числовой функцией, т.е. если
является возрастающей (строго) числовой функцией, т.е. если 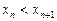
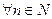 .
.
Последовательность называется убывающей (строго), если 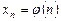 – убывающая (строго) числовая функция, т.е.
– убывающая (строго) числовая функция, т.е. 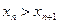
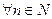 .
.
Последовательность 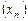 называется неубывающей, если каждый её член, начиная со второго, не меньше предыдущего, т.е.
называется неубывающей, если каждый её член, начиная со второго, не меньше предыдущего, т.е. 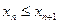
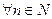 .
.
Последовательность (хn) называется невозрастающей, если каждый её член, начиная со второго, не больше предыдущего, т.е. 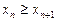
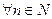 .
.
Возрастающая и убывающая последовательности называются монотонными последовательностями.
Последовательность 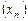 называется ограниченной, если существует такие числа m и M, что выполняется неравенство
называется ограниченной, если существует такие числа m и M, что выполняется неравенство 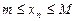
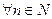 .
.
Если существует такое число M, что 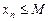
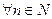 , то последовательность называется ограниченной сверху; если существует такое число m, что
, то последовательность называется ограниченной сверху; если существует такое число m, что 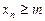
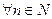 , то последовательность называется ограниченной снизу.
, то последовательность называется ограниченной снизу.
Последовательность 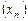 ограничена тогда и только тогда, когда существует такое положительное число C, что выполняется неравенство
ограничена тогда и только тогда, когда существует такое положительное число C, что выполняется неравенство
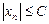
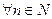 .
.
Пример 1. Определить, является ли число 28 членом последовательности 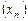 , если
, если 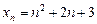 .
.
Решение. Число 28 является членом последовательности, если найдётся такой номер 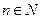 , для которого выполняется равенство
, для которого выполняется равенство 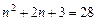 . Решим это квадратное уравнение
. Решим это квадратное уравнение 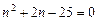 , т.е.
, т.е. 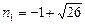 ,
, 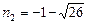 . Числа
. Числа 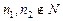 , значит, число 28 не является членом данной последовательности.
, значит, число 28 не является членом данной последовательности.
Пример 2. Вычислить первые пять членов последовательности 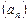 , если
, если 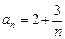 . Определить, для каких членов последовательности
. Определить, для каких членов последовательности 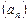 выполняется условие
выполняется условие 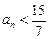 .
.
Решение. Подставляя в формулу общего члена значение n=1,2,3,4,5, получим:
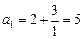 ;
; 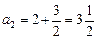 ;
;
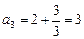 ;
; 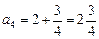 ;
;
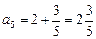 .
.
Решим неравенство 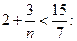
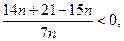
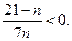
Решением этого неравенства будут 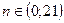 . Поэтому для любых членов последовательности с номерами от 1 до 20 включительно выполняется условие
. Поэтому для любых членов последовательности с номерами от 1 до 20 включительно выполняется условие 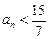 .
.
Пример 3. Последовательность задана следующим образом (реккурентно): 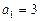 и
и 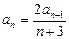 . Вычислить первые 4 ее члена.
. Вычислить первые 4 ее члена.
Решение: Первый члена последовательности известен: 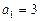 . Для вычисления
. Для вычисления 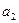 в заданной формуле для
в заданной формуле для 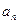 положим
положим 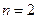 . Получим
. Получим
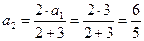 .
.
Для вычисления 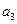 в формуле
в формуле 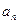 выбираем
выбираем 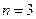 . Тогда
. Тогда 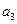 выразится через найденный член
выразится через найденный член 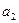 :
:
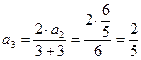 .
.
Аналогично:
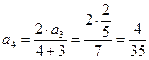 .
.
Пример 4.Последовательность 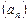 задана формулой общего члена:
задана формулой общего члена: 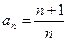 . Задать таблично первые 8 ее членов, изобразить их геометрически и графически.
. Задать таблично первые 8 ее членов, изобразить их геометрически и графически.
Решение. Вычислим первые 8 членов заданной последовательности и заполним таблицу.
| ||||||||
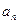
| 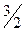
| 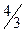
| 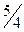
| 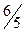
| 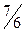
| 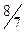
| 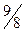
|
Для геометрической иллюстрации изобразим на числовой оси члены последовательности (рис.1)
Рис.1
В системе координат 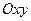 укажем точки плоскости, которые имеют координаты
укажем точки плоскости, которые имеют координаты 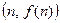 для
для 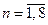 (рис.2).
(рис.2).
Рис. 2
Пример 5. Доказать, что последовательность 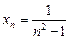 является строго убывающей.
является строго убывающей.
Решение. Если последовательность строго убывающая, то выполняется неравенство 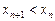 или
или 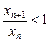
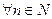 .
.
Вычисляем
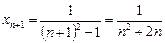 .
.
Составим отношение
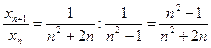 .
.
Поскольку
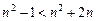
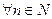 , действительно.
, действительно.
Получаем 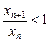 для любых натуральных n.
для любых натуральных n.
Значит, последовательность является строго убывающей.
Пример 6. Исследовать последовательность 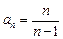 ,
, 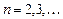 на ограниченность.
на ограниченность.
Решение. Запишем формулу общего члена последовательности следующим образом:
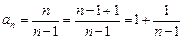 .
.
Так как 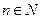 и
и 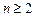 , то
, то 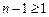 , а поэтому
, а поэтому
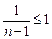 и
и 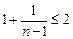 .
.
Следовательно, последовательность является ограниченной сверху.
Поскольку неравенство 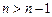 выполняется для всех
выполняется для всех 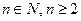 , то
, то 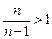 .
.
Значит, последовательность является также ограниченной снизу.
Приходим к выводу. что 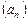 – ограниченная последовательность.
– ограниченная последовательность.
Дата добавления: 2016-07-27; просмотров: 1558;











