Различные способы задания плоскости
Вектор 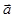 называется параллельным плоскости
называется параллельным плоскости 
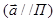 , если $
, если $ 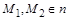 /
/ 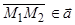 .
.
1. Пусть  - какая-либо плоскость в пространстве, точка
- какая-либо плоскость в пространстве, точка 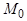 - некоторая точка этой плоскости, а векторы
- некоторая точка этой плоскости, а векторы 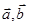 - неколлинеарны и параллельны плоскости
- неколлинеарны и параллельны плоскости  .
.
Точка 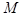 Î
Î 
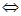 когда векторы
когда векторы 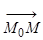 ,
, 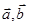 компланарны, т.е.
компланарны, т.е. 
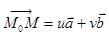 (u,v
(u,v 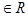 ) (1)
) (1)
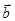
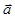
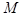
 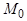
| Таким образом, чтобы задать плоскость  , достаточно задать одну её точку , достаточно задать одну её точку 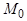 и пару неколлинеарных векторов и пару неколлинеарных векторов 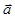 и и 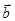 , параллельных плоскости. Плоскость , параллельных плоскости. Плоскость
|
 , заданную точкой
, заданную точкой 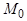 и векторами
и векторами 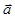 и
и 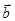 , будем обозначать:
, будем обозначать: 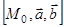
Формула (1) устанавливает взаимно однозначное соответствие между точками плоскости  и упорядоченными парами чисел
и упорядоченными парами чисел 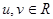 . Из определения координат точки на плоскости следует, что параметры u,v являются координатами точки
. Из определения координат точки на плоскости следует, что параметры u,v являются координатами точки 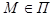 относительно аффинной системы координат
относительно аффинной системы координат 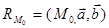 на плоскости
на плоскости  .
.
Пусть 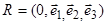 какая-либо аффинная система в пространстве и относительно неё точки
какая-либо аффинная система в пространстве и относительно неё точки 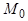 и
и 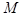 имеют координаты:
имеют координаты: 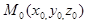 ,
, 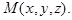 Разложим векторы
Разложим векторы 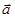 и
и 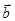 по векторам базиса
по векторам базиса 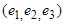 :
:
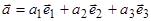 ,
, 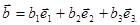


Так как векторы 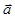 и
и 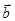 не коллинеарны, то
не коллинеарны, то
rang 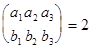 . (*)
. (*)
Сравнивая одноимённые координаты векторов в формуле (1), получим:

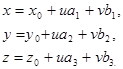 (2)
(2)
Обратно, (2) 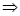 (1). Таким образом, уравнения (2) определяют плоскость
(1). Таким образом, уравнения (2) определяют плоскость  в пространстве. Они называются параметрическими уравнениямиплоскости.
в пространстве. Они называются параметрическими уравнениямиплоскости.
2. Из формулы (1) следует, что определитель системы векторов 
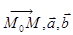 относительно базиса
относительно базиса 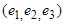 равен нулю
равен нулю 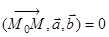
т.е. 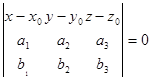 . (3)
. (3)
(3) 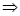
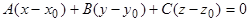 , (4)
, (4)
где 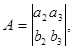
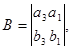
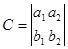 .
.
(4) 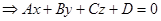 , где
, где 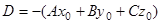 . (5)
. (5)
Уравнение (5) первой степени, так как в силу условия (*) по крайней мере одно из чисел А,В,С отлично от нуля. Следовательно, всякая плоскость определяется уравнением первой степени относительно аффинной системы координат в пространстве.
Справедливо и обратное утверждение: всякое уравнение (5) первой степени определяет некоторую плоскость в пространстве, если задана аффинная система координат 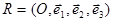 .
.
ü Так как уравнение (5) первой степени, то по крайней мере одно из чисел А,В,С отлично от нуля. Пусть А 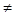 0. Тогда уравнение (5) можно представить в виде:
0. Тогда уравнение (5) можно представить в виде:
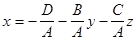 .
.
Обозначив 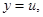
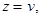 будем иметь:
будем иметь:
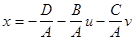 ,
,
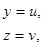
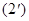
причём ранг матрицы
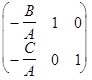 ,
,
составленный из коэффициентов при 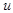 и
и 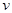 в системе
в системе 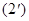 , равен двум. Следовательно, уравнения
, равен двум. Следовательно, уравнения 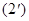 , а значит, и уравнение (5) определяют плоскость
, а значит, и уравнение (5) определяют плоскость 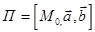 , где
, где 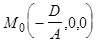 ,
, 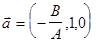 ,
, 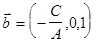 . ■
. ■
Уравнение (5) называется общимуравнением плоскости 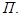 Уравнения
Уравнения 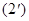 являются параметрическими уравнениями той же плоскости
являются параметрическими уравнениями той же плоскости  (при
(при 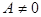 ).
).
3. Плоскость  будет определена, если задать три её точки
будет определена, если задать три её точки 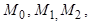 не лежащие на одной прямой:
не лежащие на одной прямой: 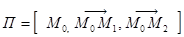 .
.
Пусть в аффинной системе координат 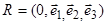 точки
точки 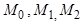 имеют координаты:
имеют координаты: 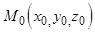 ,
, 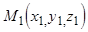 ,
, 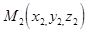 . Тогда плоскость
. Тогда плоскость  определяется уравнением:
определяется уравнением:


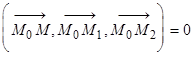
или в координатной форме:
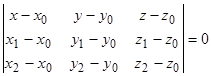 . (6)
. (6)
Если, в частности, точки 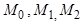 являются точками пересечения плоскости
являются точками пересечения плоскости  с осями координат
с осями координат 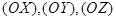 соответственно и плоскость
соответственно и плоскость  не проходит через начало координат
не проходит через начало координат 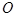 , то эти точки имеют координаты:
, то эти точки имеют координаты: 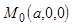 ,
, 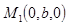 ,
, 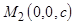 ,
, 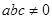 , то уравнение (6) принимает вид:
, то уравнение (6) принимает вид: 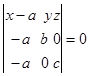 ,
,
или 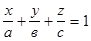 , и называется уравнениемплоскости
, и называется уравнениемплоскости  «в отрезках».
«в отрезках».
Дата добавления: 2020-10-25; просмотров: 214;










