Третья часть задания
Результаты выполнения заданий №1 и №2 представить преподавателю.
Заключение
Литература
| 1. | Атабеков Г.И. Основы теории цепей. Учебник для вузов . М., «Энергия», 1969 424с. |
| 2. | Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 600с. |
| 3. | Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. – 4-е изд., перераб. и доп. – М.: Радио и связь, 1986. – 512с.: ил. |
| 4. | Гребнев В.В. Микроконтроллеры семейства AVR фирмы Atmel. – М.: ИП РадиоСофт, 2002 – 176 с.: ил. |
| 5. | Дмитрев Б.Ф., Красавчиков В.Г., Губанов Ю.А. Математические основы и практика применения символьного метода расчета электрических цепей: Учеб. пособие/СПб.,2004.111 с. |
| 6. | Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. Издательство «Наука», Главная редакция физико-математической литературы, М., 1972. |
| 7. | Лебедев М.К. CodeVisionAVR Пособие для начинающих. – М.: Издательский дом «Додэка – XXI», 2008 – 592 с.: ил. |
| 8. | Макаров Е.Г. Инженерные расчеты в MathCad. Учебный курс. – СПб.: Питер, 2003. – 448 с.: ил. |
| 9. | Мошуц Г., Хорн П. Проектирование активных фильтров: Пер. с англ. – М.: Мир, 1984. – 320с., ил. |
| 10. | Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов том 1 М., 1978г., 456 стр. с илл. |
| 11. | Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов том 2 М., 1978г., 456 стр. с илл. |
| 12. | Татур Т.А. Основы теории электрических цепей (справочное пособие): Учеб. пособие – М.: Высш. школа, 1980. _ 271с., ил. |
| 13. | Шпак Ю.А. Программирование на языке Си для AVR и PIC микроконтроллеров. – М.: МК-Пресс, 2006 – 400 с.: ил. |
ПРИЛОЖЕНИЕ А Термины и определения
А.1 Линейные пространства
Непустое множество 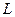 элементов
элементов 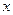 ,
, 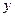 ,
, 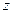 … называют линейным (или векторным) пространством, если оно удовлетворяет следующим условиям [ 9 ]:
… называют линейным (или векторным) пространством, если оно удовлетворяет следующим условиям [ 9 ]:
а) Для любых двух элементов 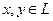 однозначно определен третий элемент
однозначно определен третий элемент 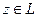 , называемый их суммой и обозначаемый
, называемый их суммой и обозначаемый 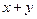 , причем:
, причем:
- 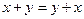 (коммутативность),
(коммутативность),
- 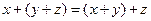 (ассоциативность),
(ассоциативность),
- в 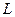 существует такой элемент
существует такой элемент 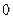 , что
, что 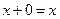 для всех
для всех 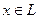 (существование нуля),
(существование нуля),
- для каждого 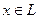 существует такой элемент
существует такой элемент 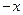 , что
, что 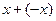 (существование противоположного элемента);
(существование противоположного элемента);
б) Для любого числа 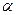 и любого элемента
и любого элемента 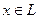 определен элемент
определен элемент 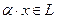 (произведение числа
(произведение числа 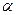 на элемент
на элемент 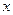 ), причем:
), причем:
- 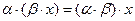 ,
,
- 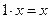 ,
,
- 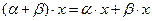 ,
,
- 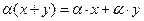 .
.
Элементы 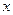 ,
, 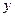 ,…
,… 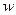 линейного пространства
линейного пространства 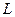 называют линейно зависимыми, если существуют такие числа
называют линейно зависимыми, если существуют такие числа 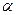 ,
, 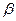 ,…
,… 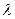 , не все равные
, не все равные 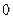 , что
, что
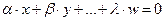 .
.
Числовую функцию 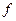 , определенную на некотором линейном пространстве
, определенную на некотором линейном пространстве 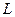 , называют функционалом.
, называют функционалом.
Функционал 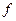 называют аддитивным, если
называют аддитивным, если
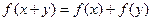 для всех
для всех 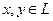 ,
,
он называется однородным, если
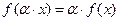 (
( 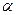 - произвольное число).
- произвольное число).
Функционал, обладающий свойством однородности, называют мультипликативным.
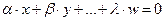 .
.
Числовую функцию 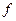 , определенную на некотором линейном пространстве
, определенную на некотором линейном пространстве 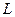 , называют функционалом.
, называют функционалом.
Функционал 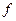 называют аддитивным, если
называют аддитивным, если
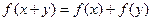 для всех
для всех 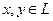 ,
,
он называется однородным, если
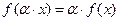 (
( 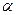 - произвольное число).
- произвольное число).
Функционал, обладающий свойством однородности, называют мультипликативным.
А.2 Дифференциальные уравнения
Дифференциальным уравнением называют уравнение [ 5 ], связывающее независимую переменную 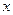 , искомую функцию
, искомую функцию 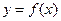 и ее производные
и ее производные 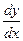 ,
, 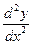 ,…,
,…, 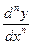
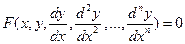 .
.
Линейным уравнением первого порядка называют уравнение, линейное относительно неизвестной функции и ее производной
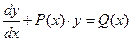 .
.
Дифференциальное уравнение n-го порядка называют линейным (уравнение первой степени относительно совокупности искомой функции и ее производных), если оно имеет вид
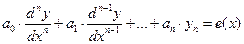 ,
,
где 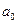 ,
, 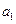 ,…,
,…, 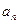 и
и 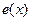 это заданные функции от
это заданные функции от 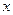 или постоянные, причем
или постоянные, причем 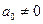 для всех значений
для всех значений 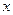 из области определения уравнения. Обычно уравнение приводят к виду с коэффициентом
из области определения уравнения. Обычно уравнение приводят к виду с коэффициентом 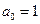 . Функцию
. Функцию 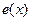 называют правой частью уравнения.
называют правой частью уравнения.
Если 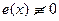 , то уравнение называют линейным неоднородным или уравнением с правой частью.
, то уравнение называют линейным неоднородным или уравнением с правой частью.
Если 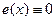 , то уравнение имеет вид
, то уравнение имеет вид
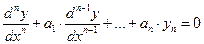
и называется линейным однородным или уравнением без правой части (левая часть этого уравнения является однородной функцией первой степени относительно 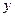 ,
, 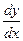 ,
, 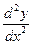 ,…,
,…, 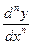 ).
).
Если для всех 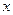 отрезка
отрезка 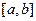 имеет место равенство
имеет место равенство
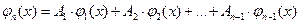 ,
,
где 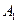 ,
, 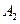 ,
, 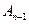 это постоянные числа, не равные нулю, то говорят, что
это постоянные числа, не равные нулю, то говорят, что 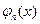 выражается линейно через функции
выражается линейно через функции 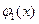 ,
, 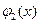 ,…
,… 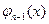 .
.
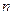 функций
функций 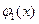 ,
, 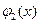 ,…
,… 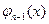 ,
, 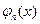 называют линейно независимыми, если никакая функция из этих функций линейно не выражается через остальные.
называют линейно независимыми, если никакая функция из этих функций линейно не выражается через остальные.
Систему дифференциальных уравнений, в которой в левой части уравнений стоят производные первого порядка, а правые части не содержат производных,
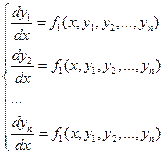 ,
,
где 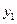 ,
, 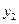 ,…
,… 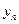 искомые функции, а
искомые функции, а 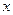 это аргумент, называют нормальной.
это аргумент, называют нормальной.
Систему дифференциальных уравнений, в которой коэффициенты 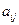 это постоянные,
это постоянные, 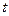 это аргумент, а
это аргумент, а 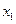 ,
, 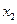 ,…
,… 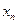 это искомые функции
это искомые функции
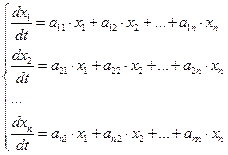 ,
,
называют системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Проинтегрировать систему дифференциальных уравнений (например, нормальную систему) это значит определить функции 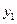 ,
, 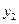 ,…
,… 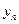 , удовлетворяющие заданной системе уравнений и начальным условиям:
, удовлетворяющие заданной системе уравнений и начальным условиям: 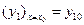 ,
, 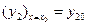 ,…
,… 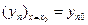 . Интегрирование нормальной системы можно производить следующим образом. Дифференцируем по
. Интегрирование нормальной системы можно производить следующим образом. Дифференцируем по 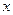 первое из уравнений
первое из уравнений
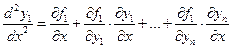 .
.
Заменяем производные 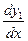 ,
, 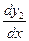 ,…
,… 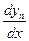 их выражениями
их выражениями 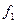 ,
, 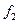 ,…
,… 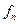 из нормальной системы уравнения получим уравнение
из нормальной системы уравнения получим уравнение
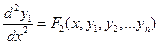 .
.
Дифференцируя полученное уравнение и делая аналогичные замены, получим уравнение
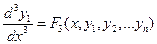 .
.
Дифференцируя далее и производя замены, получим следующую систему дифференциальных уравнений
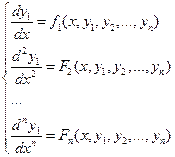 .
.
Далее из 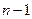 уравнений определяем
уравнений определяем 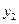 ,
, 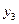 ,…
,… 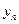 , выразив их через
, выразив их через 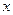 ,
, 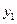 и производные
и производные 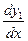 ,
, 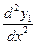 ,…
,… 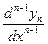 (предполагая, что эти операции выполнимы)
(предполагая, что эти операции выполнимы)
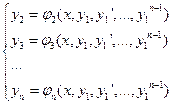 .
.
Подставив эти выражения в уравнение 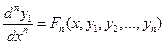 , получим уравнение n-го порядка для определения
, получим уравнение n-го порядка для определения 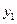
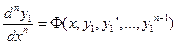 .
.
Если исходная система дифференциальных уравнений линейна относительно искомой функции, то и выражение 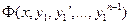 будет линейным.
будет линейным.
Решая полученное уравнение, определим 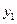 :
: 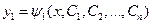 .
.
Дифференцируя это выражение 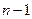 раз, найдем производные
раз, найдем производные 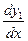 ,
, 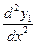 ,…
,… 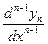 как функции от
как функции от 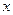 ,
, 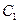 ,
, 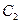 ,…
,… 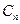 . Подставляя эти функции в уравнения для
. Подставляя эти функции в уравнения для 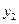 ,
, 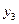 ,…
,… 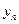 получим
получим
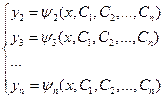 .
.
Для удовлетворения решения заданным начальным условиям необходимо найти значения постоянных 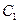 ,
, 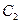 ,…
,… 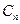 .
.
Рассмотрим пример интегрирования следующей системы дифференциальных уравнений
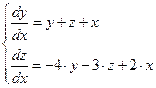
при начальных условиях 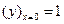 ,
, 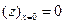 .
.
Дифференцируя по 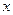 получим
получим
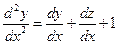 .
.
Подставив сюда выражения 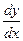 и
и 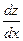 из заданных уравнений, получим
из заданных уравнений, получим
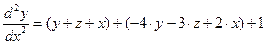
или
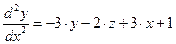 .
.
Далее, находим выражение 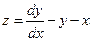 и подставляем его в только что полученное уравнение, из чего получаем
и подставляем его в только что полученное уравнение, из чего получаем
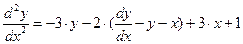
или
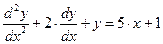 .
.
Общее решение последнего уравнения есть
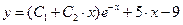
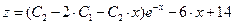 .
.
Для удовлетворения начальных условий необходимо чтобы 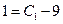 и
и 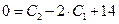 . Отсюда
. Отсюда 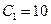 ,
, 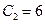 . Таким образом, решения, удовлетворяющие заданным начальным условиям, будут иметь вид
. Таким образом, решения, удовлетворяющие заданным начальным условиям, будут иметь вид
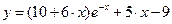 ,
,
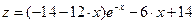 .
.
В приведенных выше рассуждениях предполагалось, что из первых 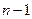 уравнений можно определить функции
уравнений можно определить функции 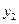 ,
, 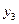 ,…
,… 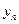 . Возможно, что переменные
. Возможно, что переменные 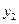 ,
, 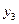 ,…
,… 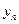 исключаются не из
исключаются не из 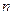 , а из меньшего числа уравнений. В этом случае получим уравнение, порядок которого ниже
, а из меньшего числа уравнений. В этом случае получим уравнение, порядок которого ниже 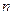 .
.
А.3 Комплексные числа
Комплексным числом называют [ 1, 2, 6 ] сумму действительного и мнимого чисел 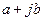 (
( 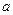 и
и 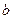 – действительные числа,
– действительные числа, 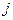 - мнимая единица). Мнимую единицу (
- мнимая единица). Мнимую единицу ( 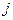 ) определяют следующим образом:
) определяют следующим образом: 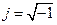 . Мнимая единица обладает свойствами:
. Мнимая единица обладает свойствами: 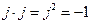 ,
, 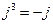 , и т.д.
, и т.д.
Два комплексных числа 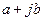 и
и 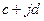 считают равными, если равны их действительные (
считают равными, если равны их действительные ( 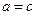 ) и мнимые (
) и мнимые ( 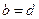 ) части.
) части.
Два комплексных числа 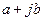 и
и 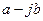 называют сопряженными.
называют сопряженными.
Комплексное число можно представить вектором на комплексной плоскости (рис. а.1), проведенным из начала координат 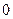 в точку
в точку 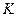 .
.
Длину вектора ( 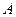 ), изображающего комплексное число, называют модулем этого числа (
), изображающего комплексное число, называют модулем этого числа ( 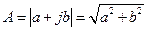 ). Аргументом комплексного числа (
). Аргументом комплексного числа ( 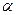 ) называют угол между осью действительных значений и вектором, изображающим комплексное число (
) называют угол между осью действительных значений и вектором, изображающим комплексное число ( 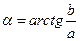 ).
).
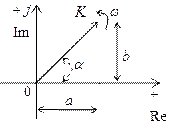
Рис. А.1 – Комплексная плоскость
Вещественную и мнимую части комплексного числа обозначают следующим образом 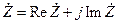 .
.
Выделяют алгебраическую, показательную и тригонометрическую формы представления комплексного числа:
- 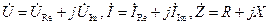 алгебраическая форма;
алгебраическая форма;
- 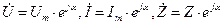 показательная форма;
показательная форма;
- 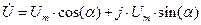 тригонометрическая форма.
тригонометрическая форма.
Алгебраическая форма удобна при сложении и вычитании комплексных чисел:
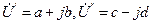 ,
,
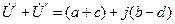 .
.
Показательная форма удобна при умножении, делении, извлечении корня и логарифмирования комплексных чисел:
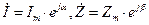 ,
,
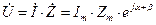 ,
,
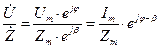 ,
,
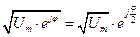 ,
,
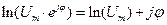 .
.
Тригонометрическая форма удобна при переходе от показательной формы к алгебраической форме комплексного числа:
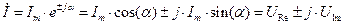 ,
,
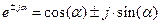 .
.
Умножение комплексного числа на величину 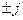 приводит к повороту вектора комплексного числа против (по) часовой стрелки на
приводит к повороту вектора комплексного числа против (по) часовой стрелки на 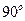 без изменения длины вектора.
без изменения длины вектора.
Сопротивление, содержащее активную и реактивную составляющую, представляют как комплексное число 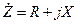 (
( 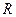 - активная,
- активная, 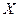 - реактивная часть).
- реактивная часть).
А.4 Гармонические функции
Гармоническим током (напряжением) называют ток, периодически изменяющийся во времени по синусоидальному закону [ 1, 6 ]. Мгновенное значение гармонического тока определяет следующим выражением
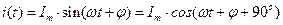 , где:
, где:
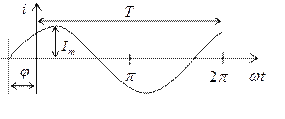
Рис. А.2 ‑ Гармоническая функция
- 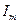 амплитуда гармонического сигнала (максимальное значение);
амплитуда гармонического сигнала (максимальное значение);
- 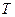 период гармонического сигнала (время одного колебания);
период гармонического сигнала (время одного колебания);
- 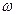 угловая частота (скорость изменения фазы);
угловая частота (скорость изменения фазы);
- 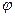 начальная фаза (значение фазы в момент времени
начальная фаза (значение фазы в момент времени 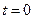 );
);
- 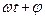 фаза (аргумент синусоидального сигнала).
фаза (аргумент синусоидального сигнала).
График гармонической функции представлен на рис. а.2.
Мгновенное значение гармонического сигнала заменяют комплексным значением, например:
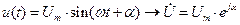 ,
,
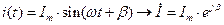 .
.
Комплексную величину, представляющую гармоническую функцию времени, отмечают точкой наверху ( 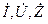 ). Иногда комплексные величины подчеркивают снизу (
). Иногда комплексные величины подчеркивают снизу ( 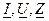 ).
).
Для описания работы линейной электрической схемы гармонического тока в установившемся режиме используют систему алгебраических уравнений, составленных по методам, основанным на законах Ома и Кирхгофа [ 3 ].
Для алгебраизации интегро-дифференциальных уравнений применяют комплексные величины. В этих уравнениях дифференцирование и интегрирование мгновенного значения переменных заменяют умножением комплексных величин этих переменных на комплексные числа 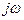 и
и 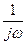 соответственно:
соответственно:
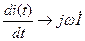 ,
, 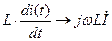
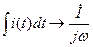 ,
, 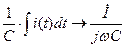 .
.
Полученную таким образом систему алгебраических уравнений можно решать относительно неизвестных комплексных величин.
А.5 Законы Ома и Кирхгофа
Для описания электрической цепи (совокупности устройств и объектов, образующих путь для электрического тока) используют некоторую эквивалентную схему. Выделяют следующие топологические элементы [ 6 ], образующие схему электрической цепи.
Ветвью называют участок электрической цепи, вдоль которого протекает один и тот же ток.
Узлом называют место соединения ветвей электрической цепи.
Контуром называют любой замкнутый путь, образованный узлами и ветвями.
Графом называют изображение схемы электрической цепи, в котором ветви схемы представлены отрезками (ветвями графа), а узлы представлены точками (узлами графа).
Деревом называют любую совокупность ветвей графа, соединяющих все узлы графа без образования контуров.
Первый закон Кирхгофа говорит о том, что алгебраическая сумма токов в узле равна или нулю или алгебраической сумме источников тока в том же узле
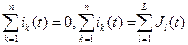 ,
,
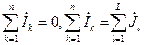 .
.
Число линейно независимых уравнений, составленных по первому закону Кирхгофа, равно n-1, где n это число узлов рассматриваемой схемы.
Второй закон Кирхгофа говорит о том, что алгебраическая сумма падений напряжений в любом замкнутом контуре схемы равна или нулю или алгебраической сумме э.д.с. в этом контуре
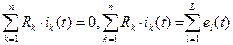 ,
,
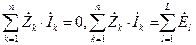 .
.
Число линейно независимых уравнений, составленных по второму закону Кирхгофа, равно m-n+1, где m это число ветвей, а n это число узлов рассматриваемой схемы.
Закон Ома для участка цепи, содержащей сопротивление, емкость и индуктивность выглядит следующим образом:
- 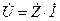 для комплексного значения гармонического тока и напряжения;
для комплексного значения гармонического тока и напряжения;
- 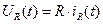 ,
, 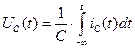 ,
, 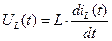 для тока и напряжения как функции времени.
для тока и напряжения как функции времени.
Формулы вычисления значений последовательного и параллельного соединения сопротивлений, представлены в табл. а.1.
Частотные и мгновенные временные характеристики цепей представлены в табл. а.2.
Табл. А.1 – Соединения сопротивлений
| Обозначение | Вычисление | Описание |

| 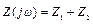
| Последовательное соединение |

| 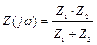
| Параллельное соединение |
Табл. А.2 – Частотные и временные характеристики цепей
| Обозначение цепи | Частотная область | Временная область |

| 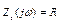
| 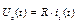
|
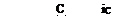 
| 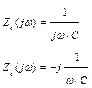
| 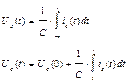
|
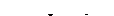 
| 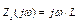
| 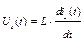
|

| 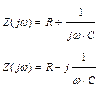
| 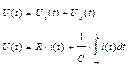
|

| 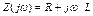
| 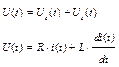
|

| 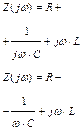
| 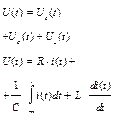
|
Рассмотрим применение законов Ома и Кирхгофа для составления алгебраических уравнений в частотной области и интегро-дифференциальных уравнений во временной области на примере схемы последовательного R, C, L контура (рис. а.3).
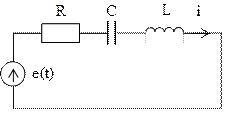
Рис. А.3 – Последовательный R, C, L контур
В частотной области, при гармоническом входном воздействии 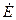 , уравнение составлено по второму закону Кирхгофа будут выглядеть следующим образом
, уравнение составлено по второму закону Кирхгофа будут выглядеть следующим образом
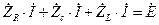 .
.
Ток в цепи вычислим по формуле 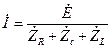 .
.
Напряжение на индуктивном элементе 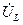 вычислим по формуле
вычислим по формуле
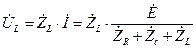
учитывая, что
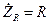 ,
, 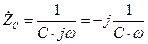 ,
, 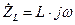
получим выражение
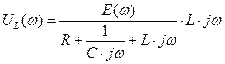 .
.
Выделив, вещественную и мнимую части выражения, получим
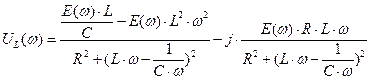
алгебраическую форму комплексного числа (зависящего от частоты 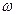 ) для напряжения
) для напряжения 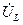 .
.
Выделив, вещественную и мнимую части выражения, получим
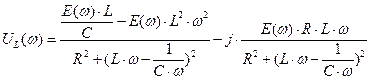
алгебраическую форму комплексного числа, зависящего от частоты 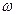 , для напряжения
, для напряжения 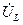 .
.
Во временной области уравнение, составленное по второму закону Кирхгофа, представлено в главе 3.2 и приложении А.6.
А.6 Переходные процессы
Переходные (нестационарные) процессы возникают в результате коммутаций, происходящих в электрических цепях. Под коммутацией понимают различные включения, выключения, переключения пассивных и активных ветвей и элементов электрической цепи, приводящие к изменению схемы или ее параметров. Считают, что коммутация совершается мгновенно. Для момента коммутации существуют следующие правила.
Ток и магнитный поток в ветви с индуктивным элементом не могут изменяться скачком, и в момент коммутации равны тем значениям, которые они имели непосредственно перед коммутацией. Условия непрерывности тока и магнитного потокосцепления в цепи с индуктивным элементом рис. а.4:
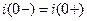 ,
, 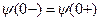 ,
, 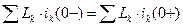 .
.
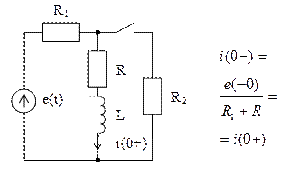
Рис. А.4 – Схема коммутации с индуктивностью
Напряжение и заряд на емкостном элементе не могут изменяться скачком, и в момент коммутации равны тем значениям, которые они имели непосредственно перед коммутацией. Условия непрерывности напряжения и заряда в цепи с емкостным элементом рис. а.5:
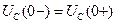 ,
,  ,
,
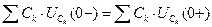 .
.
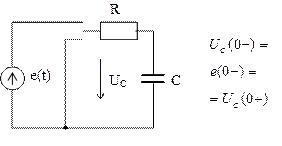
Рис. А.5 – Схема коммутации с емкостью
Независимые начальные условия (значение тока или потока в индуктивном и напряжения или заряда на емкостном элементах в момент коммутации) определяются по законам коммутации.
Зависимые начальные условия (значения токов и напряжений в момент коммутации) определяются по схеме, образованной после коммутации по законам Кирхгофа с учетом законов коммутации.
Независимые и зависимые начальные условия схемы, представленной на рис. а.6 будут следующие:
- 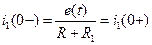 независимые начальные условия для тока
независимые начальные условия для тока 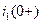 ;
;
- 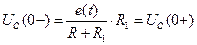 независимые начальные условия для напряжения
независимые начальные условия для напряжения 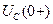 .
.
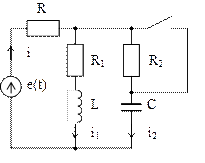
Рис. А.6 – Зависимые начальные условия
Для определения зависимых начальных условий используем законы Кирхгофа и определенные ранее значения тока и напряжения 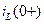 ,
, 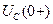 . Для цепей, образованных после коммутации, составим уравнения Кирхгофа с учетом значений
. Для цепей, образованных после коммутации, составим уравнения Кирхгофа с учетом значений 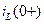 ,
, 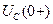 .
.
Полученную систему алгебраических уравнений решим относительно искомых величин 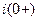 ,
, 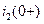 ,
, 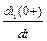 .
.
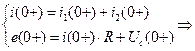
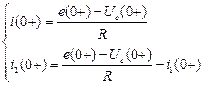
зависимые начальные условия для токов 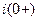 ,
, 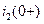 ;
;
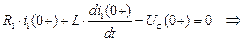
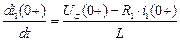
зависимые начальные условия для производной 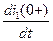 .
.
Для расчета переходных процессов на цифровых вычислительных машинах используют, как наиболее удобный, метод переменных состояний. Для после коммутационной схемы, вместо одного неоднородного дифференциального уравнения n-го порядка, решают n дифференциальных уравнений первого порядка относительно выбранных переменных. Переменными могут быть напряжения на конденсаторах, токи в индуктивных катушках, и другие величины, по начальным состояниям которых (и входным воздействиям) определяют искомые переходные функции.
В качестве примера рассмотрим переходный процесс в последовательном колебательном контуре (рис. а.3). Ток в схеме является общим для всех элементов схемы. Считаем начальные условия нулевыми 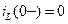 ,
, 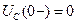 . В схеме до коммутации нет запаса энергии.
. В схеме до коммутации нет запаса энергии.
Независимые начальные условия схемы будут следующие 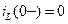 ,
, 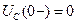
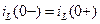 ,
, 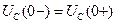 .
.
Зависимые начальные условия схемы вычисляются из следующих соображений 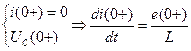 .
.
Интегро-дифференциальное уравнение контура, составленное по второму закону Кирхгофа и закону Ома, будет выглядеть так:
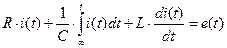 .
.
Дифференцируя левую и правую части этого уравнения, получим следующее дифференциальное уравнение второго порядка
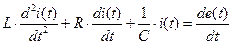 .
.
Система из двух дифференциальных уравнений первого порядка будет выглядеть так:
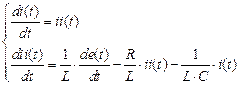 .
.
Такая система дифференциальных уравнений, решаемая численными методами, может использоваться микропроцессорной системой, для обработки входного сигнала 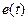 в реальном времени.
в реальном времени.
А.7 Сигналы с ограниченной полосой частот
В теории сигналов используют теорему Котельникова (теорема отсчетов). Эта теорема формулируется следующим образом [ 2 ]:
Если наивысшая частота в спектре функции 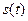 меньше чем
меньше чем 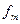 , то функция
, то функция 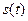 полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на
полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 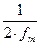 секунд.
секунд.
В соответствии с этой теоремой сигнал 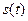 , ограниченный по спектру наивысшей частотой
, ограниченный по спектру наивысшей частотой 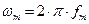 , может быть представлен рядом
, может быть представлен рядом
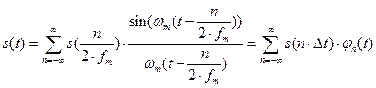 .
.
В этом выражении 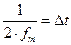 обозначает интервал между двумя отсчетными точками на оси времени, а
обозначает интервал между двумя отсчетными точками на оси времени, а 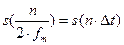 обозначает выборки функции
обозначает выборки функции 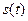 в моменты времени
в моменты времени 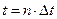 . Функция вида
. Функция вида
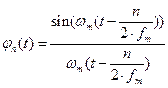
обладает следующими свойствами:
- в точке 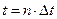 функция
функция 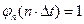 , а в точке
, а в точке 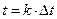 , где
, где 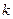 это любое целое положительное или отрицательное число, отличное от
это любое целое положительное или отрицательное число, отличное от 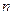 ,
, 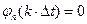 ;
;
- спектральная плотность функции 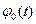 равномерна в полосе частот
равномерна в полосе частот 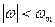 и равна
и равна 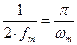 .
.
Так как функция 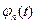 отличается от
отличается от 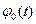 только сдвигом на оси времени на
только сдвигом на оси времени на 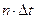 , то спектральная плотность функции
, то спектральная плотность функции 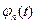 будет
будет
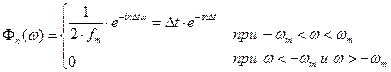 .
.
Очевидно, что ряд представляющий функцию 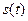 , точно определяет
, точно определяет 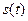 в точках отсчета поскольку коэффициентами ряда являются сами выборки из этой функции (величины
в точках отсчета поскольку коэффициентами ряда являются сами выборки из этой функции (величины 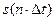 ). Для доказательства того, что ряд определяет функцию в любой момент
). Для доказательства того, что ряд определяет функцию в любой момент 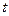 , а не только в точках отсчета
, а не только в точках отсчета 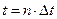 воспользуемся правилами разложения функции по ортогональной системе. В этом случае разложение производится по функциям вида
воспользуемся правилами разложения функции по ортогональной системе. В этом случае разложение производится по функциям вида 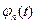 для которых интервал ортогональности равен бесконечности, а норма
для которых интервал ортогональности равен бесконечности, а норма 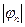 равна
равна
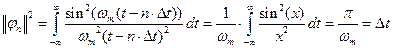 .
.
Общая формула определения значений коэффициентов ряда, справедливая для обобщенного ряда Фурье выглядит следующим образом
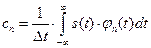 .
.
При этом предполагается, что 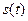 это квадратично-интегрируемая функция (энергия сигнала конечна). Для определения коэффициентов
это квадратично-интегрируемая функция (энергия сигнала конечна). Для определения коэффициентов 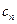 воспользуемся следующей формулой [ 2 ]
воспользуемся следующей формулой [ 2 ]
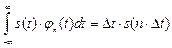 .
.
Окончательно получим следующее выражение 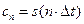 , из которого следует, что коэффициентами ряда являются выборки функции
, из которого следует, что коэффициентами ряда являются выборки функции 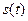 в точках
в точках 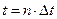 . Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции
. Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции 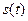 , то ряд сходится к функции
, то ряд сходится к функции 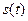 при любом значении
при любом значении 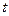 .
.
Если взять интервал между выборками 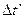 меньше чем
меньше чем 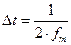 , то ширина
, то ширина 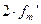 спектра
спектра 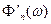 функции
функции 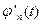 будет больше, чем у спектра
будет больше, чем у спектра 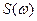 функции
функции 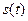 . Это повысит точность представления сигнала
. Это повысит точность представления сигнала 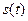 и ослабит требования к АЧХ фильтра, восстанавливающего непрерывный сигнал.
и ослабит требования к АЧХ фильтра, восстанавливающего непрерывный сигнал.
При увеличении 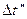 по сравнению с
по сравнению с 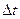 спектр
спектр 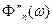 функции
функции 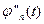 становится уже, чем спектр функции
становится уже, чем спектр функции 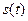 . Коэффициенты
. Коэффициенты 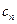 при этом являются уже выборками не заданного сигнала
при этом являются уже выборками не заданного сигнала 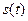 , а некоторой другой функции
, а некоторой другой функции 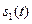 , спектр которой ограничен наивысшей частотой
, спектр которой ограничен наивысшей частотой 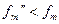 .
.
В случае, когда длительность сигнала 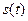 конечна и равна
конечна и равна 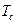 , а полоса частот по-прежнему равна
, а полоса частот по-прежнему равна 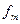 , мы имеем дело, строго говоря, с несовместимыми условиями, так как функция конечной длительности обладает теоретически бесконечно широким спектром.
, мы имеем дело, строго говоря, с несовместимыми условиями, так как функция конечной длительности обладает теоретически бесконечно широким спектром.
На практике всегда можно определить наивысшую частоту спектра 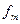 т
т
Дата добавления: 2020-10-14; просмотров: 356;