Принципы измерений и шкалирования.

Измерение – это присвоение чисел или других символов характеристикам объектов по заранее определенным правилам.

Наиболее важный аспект измерения – определение правил присвоения чисел отдельным параметрам объекта. Процесс присвоения должен быть изоморфным, т.е. должно существовать полное соответствие между числами и измеряемыми параметрами.

Например, одинаковые значения в гривнах присваиваются домохозяйствам с идентичными годовыми доходами.

Изоморфность позволяет связывать числа со специфическими характеристиками измеряемых объектов, и наоборот.

Правила присвоения чисел должны быть стандартизованными и не зависеть от объекта или времени.

Шкалирование – создание континуума (последовательного ряда), на котором размещаются измеряемые объекты.

Шкалирование можно рассматривать как продолжение измерения.

В качестве иллюстрации рассмотрим шкалу размещения потребителей согласно характеристике «отношение к кинотеатрам».

Каждому респонденту присвоим число, характеризующее отношение

- положительное (равное 1),

- нейтральное (равное 2),

- отрицательное (равное 3).

Здесь измерение – это процесс присвоения 1,2 или 3 согласно определенному правилу. Тогда шкалирование – это процесс размещения респондентов вдоль этого ряда в зависимости от отношения к кинотеатрам.

Отобранные для анализа респонденты могут рассматриваться индивидуально или попарно.

Основные типы шкал.

Мы уже отметили основные виды шкал:

- номинальная,

- порядковая,

- интервальная,

- относительная.

Охарактеризуем каждую из них.

Номинальная шкала – это шкала, числа которой служат только как ярлыки (метки) для определения и классификации объектов со строгим, один к одному, соответствием между числами и объектами.

Номинальная шкала по сути – это условная схема маркировки.

Например, присваиваемые респондентам, участникам забега. Каждый номер соответствует только одному объекту (бегуну), а каждый бегун имеет один номер.

В маркетинговых исследованиях номинальные шкалы используются для идентификации респондентов, торговых марок, магазинов и др.

Числа в номинальной шкале используют также как метки для классов и категорий. Например, математический школьный класс можно классифицировать как группу 1, а исторический – как группу 2. Классы взаимно исключающие вместе охватывают выборку. Всем объектам внутри одного класса присваивается одно и то же число.

Допустимой математической операцией с числами в номинальной шкале является счет. Допустимо только ограниченное количество статистических расчетов, базирующееся на подсчете частот.

Порядковая шкала – это ранговая шкала, в которой числа присваиваются объектам для обозначения относительной степени, в которой определенные характеристики присущи тому или иному объекту. Порядковая шкала отображает относительную позицию, но не значительность разницы между объектами.

В маркетинговых исследованиях порядковые шкалы используются для измерения отношения, мнения, восприятия, предпочтения.

Вывод: порядковая шкала – это ранговая шкала, в которой числа присваиваются объектам для отражения относительной степени выраженности некоторых характеристик у тех или иных объектов.

Порядковые шкалы можно трансформировать любым способом, если при этом сохраняется первоначальный порядок расположения.

Кроме операций подсчета, допустимых для данных номинальной шкалы, для порядковых шкал можно использовать статистические методы.

Интервальная шкала – это числовая шкала, количественно равные промежутки которой отображают равные промежутки между значениями измеряемых характеристик.

Интервальная шкала содержит всю информацию, заложенную в порядковую шкалу, кроме того она позволяет сравнивать различия между объектами.

В маркетинговых исследованиях данные об отношении покупателей, полученные по рейтинговым шкалам часто обрабатываются как интервальные.

Общеизвестный пример повседневной жизни – шкала температуры.

В интервальной шкале расположение точки начала отсчета не фиксируется. Точка начала отсчета и единицы измерения выбираются произвольно. А это значит, что преобразование

y = a + bx

Сохранит свойства шкалы (x – первоначальное значение шкалы, y – преобразованное значение шкалы, b – положительная константа).

Пусть а=20, b = 2

Мы видим, что две интервальные шкалы с числами 1, 2, 3, 4 и 22, 24, 26, 28 эквивалентны.

Статистические методы для обработки интервальных шкал включают все методы, используемые для номинальных и порядковых данных: среднее арифметическое, среднеквадратическое отклонение, коэффициент корреляции и другие, применяемые в маркетинговых исследованиях.

Относительная шкала – это наиболее информативная шкала, которая позволяет идентифицировать и классифицировать объекты, ранжировать их, а также сравнивать интервалы и разницы.

Относительная шкала обладает всеми свойствами номинальной, порядковой и интервальной шкал, кроме того, имеет точку начала отсчета.

Относительные шкалы допускают только пропорциональные преобразования вида

y = bx

где b – положительная константа.

Общеизвестные примеры относительной шкалы: рост, вес, возраст и деньги.

В маркетинге с помощью относительной шкалы измеряются объемы продаж, затраты, доля рынка и число покупателей.

Рассмотренные четыре основных вида шкал не исчерпывают всех существующих вариантов методов измерения.

1.2. СОПОСТАВАЛЕНИЕ МЕТОДОВ ШКАЛИРОВАНИЯ

Все методы шкалирования можно условно разделить на сравнительные и несравнительные.

Сравнительные шкалы – это метод шкалирования, заключающийся в прямом сравнении рассматриваемых объектов.

Например, респондентов спрашивают, предпочитают они квас или яблочный сок.

Данные сравнительных шкал являются относительными и имеют свойства только порядковых и ранговых величин.

Основное преимущество сравнительного шкалирования состоит в возможности распознавания незначительных различий между рассматриваемыми объектами.

При сравнении двух объектов респондентам приходится выбирать между ними.

Основной недостаток сравнительных шкал и порядковая природа и ограничение анализа рамками определенного количества рассматриваемых объектов.

Несравнительные шкалы – это один из методов шкалирования, заключающийся в самостоятельной оценке каждого объекта.

При использовании несравнительных шкал (иногда их называют метрическими) каждый объект исходной рассматриваемой совокупности оценивается независимо от других. Полученные данные считаются интервально или рейтингово отшкалированными.

1.3. МЕТОДЫ СРАВНИТЕЛЬНОГО ШКАЛИРОВАНИЯ

Шкалирование методом попарного сравнения –это метод сравнительного шкалирования, при котором респонденту дается два объекта для выбора по определенному критерию. Данные по своей природе порядковые.

Пример, респондент может утверждать, что он делает покупки гречневой каши чаще, чем рисовой.

Данные попарного сравнения упорядочиваются на основе свойства транзитивности.Транзитивность означает, что если торговой маркеАотдается предпочтение перед торговой маркой В, а В перед С, то А будет отдано предпочтение перед С.

Шкалирование методом попарного сравнения полезно когда количество торговых марок ограничено. В противном случае проведение попарных сравнений весьма громоздко.

Упорядоченное шкалирование –это метод сравнительного шкалирования, при котором респондентам предлагается одновременно несколько объектов с тем, чтобы они проранжировали их по определенному критерию.

Например, респондентов просят проранжировать зубные пасты по предпочтению. Например, с 1-го по 10-й ранг.

При наличии n объектов необходимо сделать лишь (n-1) решений при упорядоченном щкалировании, а при парном сравнении [n(n-1)/2] решений.

Шкалирование с постоянной суммой –это метод сравнительного шкалирования, при котором респондентов просят распределить постоянную сумму баллов между объектами сравнения по определенному критерию.

Например, респондентов просят разделить 100 очков между свойствами туалетного мыла.

Свойства объекта шкалируются делением суммы баллов, присвоенных каждому из них всеми опрашиваемыми, на общее количество респондентов.

Шкалирование методом Q-сортировки –это метод сравнительного анализа, использующий процедуру упорядочения, при которой объекты разбиваются на группы в зависимости от схожести по определенному критерию.

Это шкалирование разработано для быстрого установления различий между большим количеством объектов.

Вербальные протоколы – этот метод используется для исследования познавательных реакций или мыслительных процессов через высказывание их вслух при выполнении задания или осуществления покупки.

Протоколы используются для измерения потребительских познавательных реакций при реальных покупках. Протокольный анализ также применяется для измерения потребительской реакции на рекламу.

Например, сразу после показа рекламы респондента просят перечислить все мысли, пришедшие в голову во время просмотра. При этом, опрашиваемому дается ограниченный промежуток времени для перечисления мыслей, чтобы минимизировать вероятность включения мыслей, возникших после просмотра сообщения. После составления протокола высказывание индивида или познавательные реакции распределяются на три категории. Категории следующие: высказывание «за», высказывание «против», и недоверие источнику.

ЛЕКЦИЯ 2

Вопросы лекции:

2.1. Понятие дисперсионного анализа

2.2. Однофакторный дисперсионный анализ и его статистики

2.3. Определение зависимых и независимых переменных

2.4. Измерение эффекта

2.5. Проверка значимости

2.1. ПОНЯТИЕ ДИСПЕРСИОННОГО АНАЛИЗА

Дисперсионный анализ -это статистический метод изучения различий между выборочными средними двух или больше совокупностей.

Как правило, нулевая гипотеза утверждает, что все выборочные сведения равны.

В своей простейшей форме дисперсионный анализ должен иметь зависимую переменную (например, предпочтение к сухому завтраку), которая является метрической и измеряется с помощью интервальной или относительной шкалы. Кроме того, должна быть одна или больше независимых переменных (например, потребление продукта: сильное, среднее, слабое, полное отсутствие потребления). Все независимые переменные – их называют факторами – должны быть категориальными (неметрическими).

Из сказанного следует вывод, что фактор - это категориальная независимая переменная и что дисперсионный анализ применяется только в случае, когда все независимые переменные являются категориальными (т.е. неметрическими).

Конкретная комбинация уровней факторов называется факторным экспериментом(попросту говоря, условиями испытаний).

Различают однофакторный, двух и более факторный дисперсиионый анализ. Следовательно, однофакторный дисперсионный анализ – это метод дисперсионного анализа, при котором используется только один фактор.

Многофакторный дисперсионный анализ – это модель дисперсионного анализа, которая включает два или больше факторов.

Если набор независимых переменных состоит из категориальных и метрических переменных, то их изучают методом ковариационного анализа.

Ковариационный анализ –это специальный метод анализа дисперсий, в котором эффекты одной или больше сторонних переменных, выраженных в метрической шкале удаляют из зависимой переменной перед выполнением дисперсионного анализа.

Дисперсионный и ковариационный анализ может включать несколько независимых переменных (например степень использования продукта, лояльность к торговой марке, важность и др.).

Следует отметить, что метрическая независимая переменная, используемая в ковариационном анализе, называется ковариатой.

2.2. ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Довольно часто у маркетологов возникает необходимость установить различия в средних значениях зависимой переменной для нескольких категорий одной независимой переменной (фактора).

Этой задачей занимается однофакторный дисперсионный анализ.

Примером задач, которыми занимается однофакторный дисперсионный анализ являются:

- различаются ли разные сегменты рынка с точки зрения объема потребления товара?

- влияет ли осведомленность потребителей о магазине (высокая, средняя, низкая) на предпочтение данного магазина?

В однофакторном дисперсионном анализе используются следующие статистики:

эта-квадрат (h²) –это корреляционное отношение, с помощью которого выражают степень влияния или силу эффекта независимой переменной (фактора) Х на зависимую переменную Y. Значение – h² лежит в интервале от 0 до 1.

F-статистика.Нулевую гипотезу о том, что категориальные средние в двух выборочных совокупностях равны, проверяют с помощью F-статистики, которая представляет собой отношение межгрупповой дисперсии к дисперсии ошибки (отношение среднего квадрата Хк среднему квадрату ошибки);

средний квадрат –это сумма квадратов отклонений наблюдений, деленная на соответствующее ей число степеней свободы.

SS_между, вариация переменной Y, обусловленная различием средних между группами (межгрупповая дисперсия)(SS _betwttn, SS _x).Вариация переменной Y, связанная с вариацией средних значений категорий переменной X. Она представляет собой вариацию между уровнями переменной X или долю в сумме квадратов переменной Y, связанную с переменной X.

SS_внутри, вариация переменной Y, обусловленная вариацией внутри каждой группы категорий (внутригрупповая дисперсия)(SS _within, SS _error).Это вариация переменной Y, обусловленная изменением внутри каждой из групп переменной X. Она осуществляется за счет всех факторов, кроме X (при исключенном X).

Общая сумма квадратов SS_y.Полная дисперсия переменной Y.

Процедура выполнения однофакторного дисперсионного анализа включает:

- определение зависимых и независимых переменных;

- разложение общей вариации;

- измерение эффектов;

- проверку значимости результатов;

- интерпретацию результатов.

2.3. ОПРЕДЕЛЕНИЕ ЗАВИСИМЫХ И НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ

Пусть Y – зависимая переменная, X – независимая переменная или категориальная переменная, имеющая с категорий (уровней групп). Для каждой группы Хсуществует n наблюдений Y.

Группы Полная

выборка

X₁ X₂ X₃ X_c

Y₁ Y₁ Y₁ Y₁ Y₁

Y₂ Y₂ Y₂ Y₂ Y₂

Внутригрупповая вариация . . Полная вариация

=SS_внутри . . = SS_y

. .

Y_n Y_n Y_n Y_n Y_N

Групповые средние Y₁ Y₂ Y₃……..Y_c Y

Межгрупповая вариация = SS_между

Из таблицы видно, что размер выборки в каждой группе Х равен n, а размер общей выборки N = n x c. Для упрощений допускают, что размеры выборок в группах переменной Х (так называемые групповые размеры) равны, но это допущение необязательно.

С целью изучения различий между средними однофакторный дисперсионный анализ использует разложение полной вариации,наблюдаемой в зависимой переменной. По сути это:

разделение вариации зависимой переменной на вариацию, обусловленную различием средних внутри групп плюс вариацию, обусловленную внутригрупповой изменчивостью.

Полную вариацию зависимой переменной Y обозначаемую SS , можно разложить на два компонента

SS_y = SS_между + SS_внутри

где нижние индексы (между и внутри) относятся к группам переменной Х.

SS_между – это вариация переменной Y, связанная с различием средних между группами переменной Х. Она представляет вариацию между категориями переменной Х (межгрупповая изменчивость). Другими словами,

SS_между – это доля в сумме квадратов переменной Y, обусловленная действием независимой переменной (фактором Х). Поэтому SS_между также обозначают как SS_x.

SS_внутри – это вариация зависимой переменной Y, связанная с вариацией внутри каждой группы переменной Х, а вычисляют ее, не учитывая фактор Х. Поэтому SS_внутри также называют дисперсией ошибки, т.е. SS_ошибки.

SS_y = SS_x + SS_ошибкм

где SS_y = 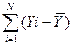²

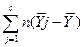SS_x = ²

SS_ошибкм = 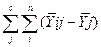²

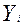- отдельное наблюдение

- среднее для группы j

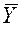- среднее для всей выборки или общая средняя

- i-наблюдение в j-группе

Смысл разложения полной вариации в переменной Y, SS_y на компоненты SS_между и SS_внутри в том, чтобы наглядно представить, а затем изучить различия в групповых средних.

2.4. ИЗМЕРЕНИЕ ЭФФЕКТА.

Сила влияния переменной Х на Y измеряется с помощью SS_x. Поскольку SS_x связано с вариацией средних значений групп Х, то относительное значение SS_x растет с увеличением различий между средними значениями Y в группах Х. Относительное значение SS_x также увеличивается при уменьшении вариаций Y внутри групп Х. Эффект влияния переменной Х на Y вычисляют по формуле

SS_x (SS_y - SS_ошибкм)

h² = ¾¾ = ¾¾¾¾¾¾¾

SS_y SS_y

Значение h² равно нулю, когда все групповые средние равны, т.е. переменная Х не влияет на Y. Значение h² равно единице, когда внутри каждой из групп переменной Х изменчивость отсутствует, но имеется некоторая изменчивость между группами. Вывод:

h² представляет собой меру вариации Y, которая объясняется влиянием независимой переменной Х.

В то же время мы в состоянии не только измерять влияние Х на Y, но и проверить его значимость.

2.5. ПРОВЕРКА ЗНАЧИМОСТИ.

В однофакторном дисперсионном анализе проверяют нулевую гипотезу, утверждающую, что групповые средние в рассматриваемой совокупности равны. Т.е. H₀ :m₁ = m₂ = m₃ =………= m_с

В соответствии с нулевой гипотезой значение SS_x и SS_ошибкм зависят от одного источника вариации. В этом случае оценка дисперсии совокупности Y может определяться межгрупповой или внутригрупповой вариации, т.е.

SS_x

S_y² = ¾¾¾¾;

(с-1)

что представляет собой средний квадрат, обусловленный действием Х, который можно записать по другому МS_x.

В то же время оценка дисперсии совокупности Y

SS_ошибкм

S_y² = ¾¾¾¾;

(N-c)

что представляет собой средний квадрат, обусловленный действием всех факторов кроме Х, что можно записать как МS_ошибкм.

Нулевую гипотезу H₀ можно проверить с помощью F-статистики, рассчитываемой как отношение между этими двумя оценками дисперсий:

SS_x / (с-1) МS_x

F = ¾¾¾¾¾¾¾ = ¾¾¾¾

SS_ошибкм / (N-c) МS_ошибкм

Эта статистика подчиняется F-распределению с числом степеней свободы равным (с-1) и (N-c). Напомним, что F-распределение представляет собой распределение вероятностей отношений выборочных дисперсий. Значение F зависит от числа степеней свободы в числителе и знаменателе.

Интерпретация результатов.

Если нулевую гипотезу о равенстве групповых средних не отклоняют, то независимая переменная не оказывает статистически значимого влияния на зависимую переменную.

Понятно, что если нулевую гипотезу отклонить, то эффект независимой переменной на зависимую трактуется как статистически значимый, т.е. среднее значение зависимой переменной различно для различных групп независимой переменной.

Необходимо отметить, что сравнение значений групповых средних показывает характер влияния независимой переменной.

ЛЕКЦИЯ 3

Вопросы лекции:

3.1. Допущения в дисперсионном анализе

3.2. Многофакторный дисперсионный анализ

3.3. Ковариационный анализ

3.4. Парная корреляция

3.5. Частная корреляция

3.1. ДОПУЩЕНИЯ В ДИСПЕРСИОННОМ АНАЛИЗЕ.

Все допущения дисперсионного анализа можно обобщить в следующем виде.

1. Обычно считается, что уровни независимой переменной фиксированные. Статистический вывод касается только рассматриваемых конкретных уровней. Такой подход называется моделью с фиксированным влиянием уровней фактора. Однако существуют и другие модели. Так, например, для модели со случайным влиянием уровней фактора считают, что факторы представляют собой случайные выборки из генеральной совокупности факторного эксперимента. Модель со смешанными уровнями получают,если некоторые факторы (условия эксперимента) фиксированные, а некоторые – случайные.

2. Предварительно отметим, что однофакторная дисперсионная модель имеет вид

x_ij = m + F_i + e_ij ,

где x_ij – значение исследуемой переменной, полученной на i-м уровне фактора (i = 1, 2,…,m) с j-м порядковым номером (j = 1, 2,…, n);

m - общее среднее;

F_i- эффект, обусловленный влиянием i-го уровня фактора;

e_ij – остаточный член, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменной внутри отдельного уровня.

Так вот, остаточный член в дисперсионной модели, определяющей значение зависимой переменной Y, имеет нормальное распределение, при этом, математическое ожидание равно нулю, а дисперсия является постоянной. Остаточный член не связан ни с одним уровнем переменной Х. Умеренное отклонение от этих допущений серьезно не влияет на достоверность анализа. Более того, данные можно преобразовать таким образом, чтобы они удовлетворяли допущению о нормальности распределения или постоянству дисперсий.

3. Остаточные члены не коррелируют. Если остаточные члены взаимосвязаны (т.е. наблюдения зависимые), то отношение дисперсий F может быть сильно искажено.

Очень часто при анализе ситуаций данные соответствуют описанным выше трем допущениям. Поэтому дисперсионный анализ достаточно распространен на практике.

3.2. МНОГОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Часто при исследованиях приходится иметь дело с одновременным влиянием нескольких факторов. Например – влияет ли на выбор потребителем конкретной торговой марки уровень образования и возраст?

Главное преимущество МДА в том, что он позволяет изучать взаимодействие факторов. Взаимодействия имеют место, когда эффекты одного фактора на зависимую переменную зависят от уровня других факторов.

Взаимодействие имеет место при оценке зависимости между двумя переменными, если влияние Х₁ зависит от уровня Х₂ и наоборот.

Сама процедура МДА аналогична процедуре однофакторного дисперсионного анализа. Статистики, соответствующие МДА также определяются аналогично определению статистик в ОДА.

Рассмотрим пример, в который входят факторы Х₁ и Х₂ с уровнями с₁ и с₂ соответственно. В этом случае полная вариация раскладывается следующим образом.

SS_полная = SS

за счет Х₁ + SS, Х₂ + SS и взаимодействия Х₁ и Х₂ + SS_внутри

Эту формулу можно записать по другому

SS_y = SS_x1 + SS_x2 + SS_x1x2 + SS_ошибкм

Большое влияние Х₁ будет выражаться в большом отличии среднего в уровнях Х₁ , а также более высоком значении SS_x1. Это же касается и фактора Х₂. Чем сильнее взаимодействие между факторами Х₁ и Х₂, тем больше значение SS_x1x2. С другой стороны, если Х₁ и Х₂ не зависят один от другого, то значение SS_x1x2 приближается к нулю.

Степень объединенного влияния, т.е. эффекта двух факторов называют полным эффектом или множественной корреляцией h², которая вычисляется по формуле.

(SS_x1 + SS_x2 + SS_x1x2)

h² = ¾¾¾¾¾¾¾¾¾¾

SS_y

Значимость полного эффектапроверяется с помощью F-критерия

(SS_x1 + SS_x2 + SS_x1x2)/df_n SS_x1._x2._x1x2/ df_n MS_x1._x2._x1x2

F = ¾¾¾¾¾¾¾¾¾¾¾ = ¾¾¾¾¾¾¾¾¾¾ = ¾¾¾¾¾¾;

SS_ошибкм/df_d SS_ошибкм/df_d MS_ошибкм

где df_n – число степеней свободы для числителя, которое равно

(с₁ – 1) + (с₂ – 1) + (с₁ – 1) (с₂ – 1) = с₁с₂ -1

df_d – число степеней свободы для знаменателя, которое равно

N - с₁с₂

M – средний квадрат.

Проверка наличия различий между некоторыми из групп факторного эксперимента определяет значимость полного эффекта.

Если полный эффект статистически значимый, то на следующем этапе изучают значимость эффектов взаимодействия.

Если нулевая гипотеза утверждает, что взаимодействие между факторами отсутствует, то соответствующий F-критерий вычисляют по формуле

SS_x1x2/ df_n MS_x1x2

F = ¾¾¾¾¾¾¾ = ¾¾¾¾¾¾;

SS_ошибкм/df_d MS_ошибкм

где df_n = (с₁ – 1) + (с₂ – 1)

df_d = N - с₁с₂

Значимость эффекта взаимодействиявыявляется с помощью проверки взаимодействия между двумя или больше независимыми переменными. При этом, если окажется, что эффект взаимодействия статистически значимый, то эффект Х₁ зависит от Х₂ и наоборот. Поскольку эффект, т.е. влияние одного фактора является неоднородным, а зависит от уровня другого фактора, то проверять значимость главных эффектов бессмысленно. В то же время имеет смысл проверить значимость главного эффекта каждого фактора, если эффект взаимодействия статистически незначимый.

Значимость главного эффекта каждого фактора, например, для Х₁ можно проверить следующим образом

SS_x1/ df_n MS_x1

F = ¾¾¾¾¾¾¾ = ¾¾¾¾¾¾;

SS_ошибкм/df_d MS_ошибкм

где df_n = с₁ – 1

df_d = N - с₁с₂

Все вышесказанное справедливо только тогда, когда план эксперимента сбалансированный, т.е. число случаев в каждой ячейке одинаково. В противном случае дисперсионный анализ усложняется.

При проверке различий в средних значениях зависимой переменной, связанных с влиянием контролируемых независимых переменных, часто необходимо учитывать неконтролируемые независимые переменные. Например, при определении влияния различных цен на потребление в семьях сухих завтраков может оказаться существенным такой фактор, как размер семьи. Для решения подобных задач служит

3.3. КОВАРИАЦИОННЫЙ АНАЛИЗ

По сути дела эта дисперсионный анализ, который включает, по крайней мере, одну категориальную независимую переменную и одну интервальную или метрическую независимую переменную.

Категориальную независимую переменную называют фактором, а метрическую – ковариатой. Обычно ковариату используют для удаления посторонней вариации из зависимой переменной, поскольку самыми важными являются эффекты факторов. Вариацию в зависимой переменной, обусловленную ковариатой, удаляют корректировкой среднего значения зависимой переменной в пределах каждого условия эксперимента. Затем, базируясь на скорректированных оценках, выполняют дисперсионный анализ. Значимость суммарного эффекта ковариат равно как и эффект каждой ковариаты, проверяют с помощью соответствующих F-критериев. Коэффициенты ковариат позволяют понять влияние, которое оказывается на зависимую переменную.

Ковариационный анализ наиболее целесообразен для применения тогда, когда ковариата линейно связана с зависимой переменной и при этом не связана с факторами.

3.4. ПАРНАЯ КОРРЕЛЯЦИЯ

Зачастую исследователя интересует связь между двумя метрическими переменными, например, связано ли восприятие качества товаров потребителями с их восприятием цены?

В подобных ситуациях наиболее широко используемой статистикой является коэффициент парной корреляции r, который характеризует степень тесноты связи между двумя метрическими переменными, например, Х и Y. Эта степень связи измеряется с помощью интервальной или относительной шкал.

Коэффициент корреляции показывает степень, в которой вариация одной переменной Х связана с вариацией другой переменной Y.

Получив выборку, размером n наблюдений, коэффициент корреляции для переменных Х и Y можно вычислить по формуле

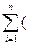X 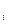- 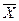)(Y_i - )

r = ¾¾¾¾¾¾¾¾¾¾¾

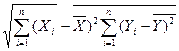
Разделив числитель и знаменатель на (n-1) получим

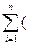X - )(Y_i - )

n-1

r = ¾¾¾¾¾¾¾¾¾¾ = COV_xy / S_xS_y

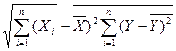
n-1 n-1

В этих уравнениях 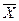и обозначают выборочные средние, а S_x и S_y – соответствующие стандартные отклонения. COV_xy – это ковариация между Х и Y, т.е. мера зависимости между Х и Y.

Ковариация – это систематическая взаимосвязь между двумя переменными, при которой изменения одной переменной вызывает соответствующее изменение другой переменной.

Ковариация может быть как положительной, так и отрицательной. Деление ковариации на S_xS_y осуществляет нормировку, откуда видно, что коэффициент корреляции r находится в пределах от минус 1 до плюс 1. очевидно, что коэффициент корреляции никак не связан с единицами измерения, в которых выражены переменные, т.е. является безразмерной величиной.

3.5. ЧАСТНАЯ КОРРЕЛЯЦИЯ

ЛЕКЦИЯ 4

Вопросы лекции:

4.1. Условия, которые допускают использование регрессионного анализа.

4.2. Парная регрессия.

4.3. Стадии парного регрессионного анализа.

4.4. Поле корреляции.

4.5. Определение параметров уравнения регрессии.

4.6. Нормированный коэффициент регрессии и проверка значимости.

4.1. УСЛОВИЯ, КОТОРЫЕ ДОПУСКАЮТ ИСПОЛЬЗОВАНИЕ РЕГРЕССИОННОГО АНАЛИЗА

Это статистический метод установления формы и изучения связей между метрической зависимой переменной и одной или несколькими независимыми переменными.

Как правило, регрессионный анализ используют в следующих случаях.

1. Действительно ли независимые переменные обуславливают значимую вариацию зависимой переменной. Другими словами, действительно ли эти переменные взаимосвязаны?

2. В какой степени вариацию зависимой переменной можно объяснить независимыми переменными (здесь идет разговор о тесноте связи)?

3. Требуется определить форму связи, т.е. математическое уравнение, описывающее зависимость между зависимой и независимой переменными.

4. Требуется предсказать значения зависимой переменной.

5. Требуется контролировать другие независимые переменные при определении вкладов конкретной переменной.

В регрессионном анализе используются такие термины, как зависимая или критериальная переменнаяи независимая переменная (предиктор). Эти термины отражают наличие математической зависимости между переменными.

Рассмотрим последовательно сперва парную, а затем множественную регрессию.

4.2. ПАРНАЯ РЕГРЕССИЯ

Это метод установления математической зависимости между одной метрической зависимой (критериальной) переменной и одной метрической независимой переменной (предиктором). В значительной мере этот анализ аналогичен определению простой корреляции между двумя переменными. Однако для того, чтобы вывести уравнение, необходимо одну переменную представить как зависимую, а другую как независимую.

С парным регрессионным анализом связаны следующие статистики.

Мы приведем статистики и термины, относящиеся к парному регрессионному анализу.

Модель парной регрессии.Основное уравнение регрессии имеет вид

Y_i = b_o + b₁X_i + e_i,

где Y – зависимая или критериальная переменная,

Х - независимая переменная или предиктор,

b_o – точка пересечения прямой регрессии с осью OY,

b₁ – тангенс угла наклона прямой,

e_i – остаточный член (остаток), связанный с i-м наблюдением, характеризующий отклонение от функции регрессии.

Примечание: в отдельных источниках этот член уравнения называют также ошибочным (ошибкой) или возмущающим членом (возмущением).

Коэффициент детерминации.Тесноту связи измеряют коэффициентом детерминации r² . Он колеблется в диапазоне между 0 и 1 и указывает на долю полной вариации Y, которая обусловлена вариацией Х.

Вычисляемое (теоретическое) значение Y.Вычисляемое значение Y ра