Обобщенные многочлены наилучших среднеквадратических приближений

Вернемся к общей постановке задачи аппроксимации функций.

Пусть аппроксимируемая функция f(x) и аппроксимирующая функция j(x) непрерывны на отрезке [a, b] и аппроксимация должна производиться так, чтобы функция j(x) «в среднем хорошо описывала» поведение функции f(x) при x Î [a, b]. Будем здесь постоянно иметь в виду две аппроксимационные ситуации: первая, это когда функция f(x) считается (по крайней мере, теоретически) известной в любой точке x отрезка [a, b], и близость между f(x) и j(x) понимается в интегральном смысле, и вторая, когда f(x) известна (причем приближенно) только в n + 1 точках x₀, x₁, …, x_n отрезка [a, b], в которых и производится согласование f(x) с j(x) подобно тому, как это делалось в рассмотренной выше задачи. В связи с этим, будем параллельно рассматривать:

а) пространство C_L[a, b] непрерывных на [a, b] функций со скалярным произведением

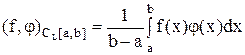(4)

метрикой (расстоянием)

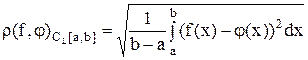(5)

и нормой

,

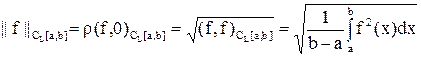б) пространство R_n+1[a, b] сеточных функций, определенных в точках x_i Î [a, b] (i = 0, 1, …, n), со скалярным произведением

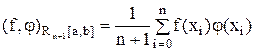(6)

метрикой

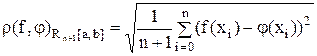(7)

и нормой

.

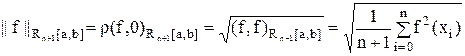Введенные указанным способом метрики (5) и (7) характеризуют близость функций f(x) и j(x) в пространствах C_L[a, b] и R_n+1[a, b] соответственно; по отношению к приближенному равенству f(x) » j(x) при x Î [a, b] они представляют собой интегральную и точечную (дискретную) среднеквадратические ошибки.

В силу того, что

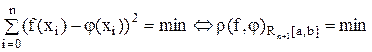
и

,

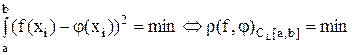можно сказать, что применение метода наименьших квадратов к аппроксимации функции f(x) функцией j(x) заданного семейства означает подбор такой функции j(x), которая минимизирует среднеквадратическую погрешность приближенного равенства f(x) » j(x) в интегральном или в точечном смысле; в связи с этим, она называется наилучшим среднеквадратическим приближением f(x) на заданном семействе функций.

Рассмотрим, к чему сводится процесс построения наилучших среднеквадратических приближений в одном конкретном, но достаточно общем случае, когда аппроксимирующая f(x) функция j(x) представляет собой линейную комбинацию нескольких других, вообще говоря, более простых (базисных) функций.

Пусть 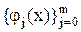— некоторая заданная на [a, b] система линейно независимых функций. Обобщенным многочленом будем называть функцию

Q_m(x) = c₀j₀(x) + c₁j₁(x) + … + c_mj_m(x), (8)

где c₀, c₁, …, c_m — произвольные вещественные числа (коэффициенты обобщенного многочлена). Поскольку функции j_j(x) считаются заданными, построение обобщенного многочлена наилучшего среднеквадратического приближения для данной функции f(x) сводится к нахождению оптимального набора c₀*, c₁*, …, c_m* коэффициентов Q_m(x) в (8) на основе метода наименьших квадратов, т. е. к решению задач минимизации:

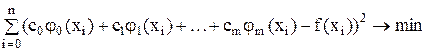(9)

— в дискретном случае;

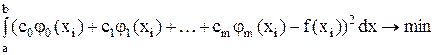(10)

— в непрерывном случае.

Для первой из этих задач, т. е. для (9), необходимые (и достаточные) условия выражаются системой

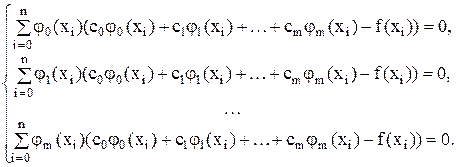(11)

После элементарных преобразований она может быть переписана в терминах скалярных произведений (см. (7)):

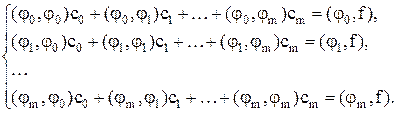(12)

Если сеточные функции j_j(x_i) образуют систему линейно независимых элементов пространства R_n+1[a, b], то полученная симметричная линейная алгебраическая система (12), называемая нормальной системой МНК, имеет заведомо отличный от нуля определитель (это известный определитель Грама), и значит, однозначно разрешима. Следовательно, при заданном базисе {j_j} путем решения системы (12) можно найти единственный обобщенный многочлен

Q_m*(x) = c₀*j₀(x) + c₁*j₁(x) + … + c_m*j_m(x)

такой, что f(x) » Q_m*(x) при x Î [a, b] с наименьшей среднеквадратической ошибкой

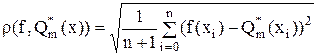(13)

Вернемся вновь на начальный этап построения обобщенного многочлена наилучшего среднеквадратического приближения, но теперь уже в интегральном смысле. Легко убедиться, что записав для задачи (10) необходимые условия, т.е. получив интегральный аналог системы (11), от нее приходим к той же самой нормальной системе МНК (12), только скалярные произведения здесь расшифровываются с помощью формулы (4). Для той же f(x) и при том же базисе {j_j}, ввиду различий в скалярных произведениях (4) и. (6), решение системы (12) в этом случае дает, вообще говоря, уже другой (возможно, «близкий» к c₀*, c₁*, …, c_m*) оптимальный набор 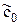, , 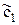…, 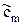коэффициентов (8) и приводит к представлению

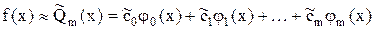
с наименьшим среднеквадратическим отклонением

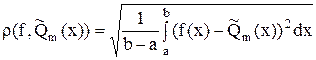(14)

(т. е. гарантируется, что , где Q_m(x) — произвольная функция вида (8)).

Анализируя СЛАУ (12), приходим к выводу, что она чрезвычайно упрощается в случае, когда базисные функции j_j(x) образуют на [a, b] ортогональную систему.

Как известно, взаимная ортогональность функций из множества 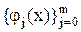означает, что (j_j, j_k) = 0 при любых k ¹ j.

Следовательно, коэффициенты c₀, c₁, …, с_m обобщенного многочлена наилучшего среднеквадратического приближения (8) могут быть сразу выписаны из превратившейся в диагональную системы (12), а именно:

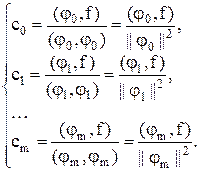(15)

В таком случае эти оптимальные коэффициенты называются коэффициентами Фурье, а обобщенный многочлен (8) с этим набором коэффициентов (т.е. обобщенный многочлен наилучшего среднеквадратического приближения для f(x)) называется обобщенным многочленом Фурье.

Еще проще построение таких многочленов, когда система 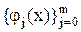— ортонормированная. Тогда ||j_j|| = 1, и из (15) следует, что c_j = (j_j, f) при любом j Î {0, 1, …, m}, т. е. аппроксимация функции f (x) обобщенным многочленом Фурье имеет вид

f(x) » (j₀, f)j₀(x) + (j₁, f)j₁(x) + … + (j_m, f)j_m(x). (16)

В частности, в математическом анализе достаточно подробно изучаются представления функций (не обязательно непрерывных) выражениями типа (16), в которых в качестве базисных функций используются функции ортогональной на [–p, p] системы {sin kx, cos kx| k Î N₀}. Такие представления в этом случае называются отрезками тригонометрических рядов Фурье.