Метод наименьших квадратов
Предположим, что между независимой переменной x и зависимой переменной y имеется некая неизвестная функциональная связь у = f(x). Эта связь отображается таблицей
| x | x0 | x1 | … | xn |
| y | y0 | y1 | … | yn |
приближенных значений yi » f(xi), получаемых в ходе наблюдений или экспериментов. Требуется дать приближенное аналитическое описание этой связи, т. е. подобрать функцию j(x) такую, которая аппроксимировала бы на отрезке [x0, xn] заданную отдельными приближенными значениями yi функцию f(x).
Для решения этой задачи заведомо неудачным является интерполяционный подход хотя бы потому, что функция j(x) такая, что j(xi) = yi при всех i Î {0, 1, …, n}, будет мало похожа на искомую f(x), поскольку в ней отразятся все ошибки экспериментальных данных. Уже это заставляет отказаться от идеи интерполяции и находить функцию j(x) такую, чтобы она хорошо отражала «в среднем» зависимость между x и у.
Конкретнее, из каких-либо соображений (аналитических, графических или иных) аппроксимирующая f(x) функция j(x) берется из определенного m-параметрического семейства функций, и ее параметры подбираются так, чтобы сумма квадратов отклонений вычисляемых значений j(xi) от заданных приближенных значений yi была минимальной. Такая функция (т. е. при таком оптимальном наборе параметров) будет наилучшей аппроксимацией f(x) среди функций выбранного семейства в смысле метода наименьших квадратов. Ясно, что число данных приближенных значений yi в таблице должно быть не меньшим, чем число параметров в подбираемой зависимости j(x); как правило, считается, что n >> m.
Итак, согласно МНК, задаем семейство
у = j(x, a1, a2, …, am)
и ищем значения параметров a1, a2, …, am (где m £ n – 1), решая экстремальную задачу
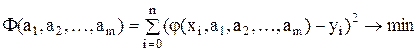 .
.
Оптимальный набор параметров a1*, a2*, … am* может быть найден из системы
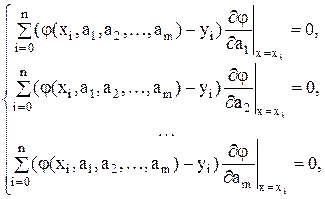 (1)
(1)
представляющей необходимые условия экстремума функции j(x, a1, a2, …,am), в силу ее специфики, являющиеся и достаточными условиями ее минимума.
Если функция j(x, a1, a2, …, am) есть линейная функция относительно своих параметров a1, a2, …, am, то система (1) тоже будет линейной; в общем случае (1) — нелинейная система, что влечет за собой определенные трудности при ее решении. Спасительным в последней ситуации является тот факт, что обычно при задании семейств функций, аппроксимирующих реальные зависимости, число параметров берется небольшим (2-3), причем какие-то из этих параметров могут входить линейным образом.
В зависимости от характера табличных данных, изучаемого с помощью их изображения в соответствующей системе координат или с помощью некоторых прикидочных расчетов, при обработке результатов экспериментов часто используют те или иные из следующих двухпараметрических семейств функций:
y = ax + b, y = a + b ln x (y = a + b lg x), y = axb, y = aebx (у = а×10bx),
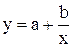 ,
, 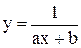 ,
, 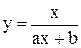 ;
;
реже применяются трехпараметрические семейства
у = ax2 + bx + c, у = axb + с, y = aebx + c (у = а×10bx + с);
при изучении периодических явлений применяют тригонометрические функции.
В качестве примера рассмотрим ситуацию, когда есть основания считать, что значения xi и соответствующие им приближенные значения yi отражают некую линейную зависимость. Тогда, полагая
j(x, a, b) = ax + b,
находим 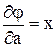 ,
, 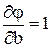 , и для вычисления параметров этой функции φ составляем систему типа (1):
, и для вычисления параметров этой функции φ составляем систему типа (1):
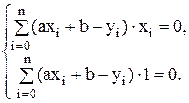
Упрощая ее, приходим к стандартной СЛАУ
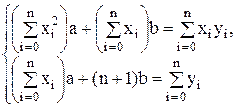 (2)
(2)
с симметричной квадратной матрицей коэффициентов и заведомо однозначным решением (а; b).
Заметим, что вместо того, чтобы решать нелинейные системы, получающиеся из (1) при поиске параметров конкретных семейств функций, когда эти параметры входят туда нелинейным образом, можно попытаться сначала линеаризовать подбираемую зависимость.
Пусть, например, в качестве аппроксимирующей f(x) функции берется экспоненциальная функция
Ф(x, а, b) = aebx. (3)
Найдя ее частные производные
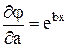 ,
, 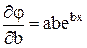 ,
,
видим, что подстановка этой функции и ее производных по параметрам в (1) приведет к нелинейной относительно параметра b системе. Чтобы не решать нелинейных уравнений, поступим так. Прологарифмируем равенство aebx = y, получив при этом
ln a + bx = ln у,
введем новый параметр A = ln а и пересчитаем данную таблицу, переведя значения yi в Yi = ln yi. По таблице
| x | x0 | x1 | … | xn |
| Υ | Y0 | Y1 | … | Yn |
методом наименьших квадратов находим оптимальные параметры A* и b* линейной функции Υ = A + bx (полагая j1(x, А, b) = А + bx, пользуемся системой (2), считая там a = b, a b = А). После этого вычисляем оптимальное значение a* = eA* параметра a исходной зависимости (3) и записываем итоговый результат
f(x) » a*eb*x.
Дата добавления: 2022-04-12; просмотров: 219;











