Погрешность вычислений

Пусть A и а — два «близких» числа; условимся считать A — точным, а — приближенным.

Определение 1. Абсолютная и относительная погрешность.

Величина Δa = |A – а| называется абсолютной погрешностью приближенного числа а, а 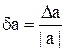его относительной погрешностью. Числа Δ_a и δ_a такие, что D_a³Da и 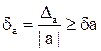, называются оценками или границами абсолютной и относительной погрешностей соответственно (к Δ_a и δ_a часто применяют также термин «предельные погрешности»).

Так как обычно истинные погрешности не известны, то там, где не может возникнуть недоразумений, будем иногда называть Δ_a и δ_a просто абсолютной и относительной погрешностями.

Определение 2. Значащие цифры.

Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 1. Значащие цифры.

У чисел a = 0,03045, а = 0,03045000 значащими цифрами являются подчеркнутые цифры. Число значащих цифр в первом случае равно 4, во втором — 7.

Определение 3. Верная цифра.

Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример 2. Верная цифра.

а = 0,03045, Δa = 0,000003; а = 0,03045000, Δa = 0,0000007; подчеркнутые цифры являются верными.

Определение 4. Все верные цифры.

Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Пример 3. Все верные цифры.

При a = 0,03045, Δa = 0,000003 число a записано со всеми верными цифрами.

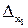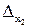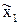Поставим вопрос о грубом оценивании погрешности результата вычисления значения дифференцируемой функции u = f(x₁, x₂, …, x_n) приближенных аргументов x₁, x₂, …, x_n, если известны границы их абсолютных погрешностей , , …, , соответственно. В этом случае точные значения аргументов , , …, лежат соответственно на отрезках 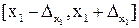, , 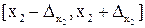…, , 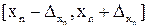а точная абсолютная погрешность результата u = f(x₁, x₂, …, x_n) есть

—

модуль полного приращения функции. Главной, т.е. линейной частью этого приращения является, как известно, полный дифференциал du. Таким образом, имеем:

,

т.е. за границу абсолютной погрешности результата приближенно может быть принята величина

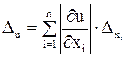. (1)

Отсюда легко получается формула приближенной оценки относительной погрешности значения u:

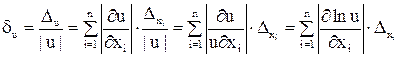. (2)

Как частные случаи формул (1), (2) (точных для функций, линейных относительно x_i или ln x_i соответственно) можно получить известные правила оценивания погрешностей результатов арифметических действий.

Действительно, пусть u = ± x₁ ± x₂ ± … ± x_n. Тогда и 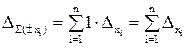, т.е. при сложении и вычитании приближенных чисел их предельные абсолютные погрешности складываются.

Пусть теперь u = x₁ × x₂ × … × x_n, где можно считать все сомножители положительными. Так как ln u = ln x₁ + ln x₂ + … + ln x_n и , то, согласно (2),

(3)

Если же 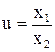, где x₁, x₂ > 0, то ln u = ln x₁ – ln x₂, 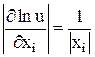и, значит,

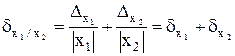
Последнее вместе с (3) означает известный результат о сложении предельных относительных погрешностей при умножении и делении приближенных чисел.

Возвращаясь к сложению, рассмотрим относительную погрешность суммы n положительных приближенных чисел x₁, x₂, …, x_n, имеющих границы относительных погрешностей , , …, 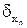соответственно:

,

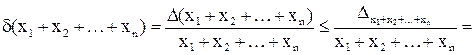
где 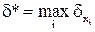. Полученное неравенство говорит о том, что относительная погрешность суммы n положительных приближенных чисел не превосходит максимальной относительной погрешности слагаемых.

С вычитанием приближенных чисел дело обстоит хуже: оценка

относительной погрешности разности x₁ – x₂ двух приближенных положительных чисел указывает на возможность сильного возрастания погрешности при x₁ – x₂ ® 0. В этом случае говорят о потере точности при вычитании близких чисел.

Часто возникает обратная задача теории погрешностей: какой точности данные нужно подать на вход, чтобы на выходе получить результат заданной точности? Применительно к поставленной выше прямой задаче оценивания погрешности результата вычисления значения функции при заданных оценках погрешностей аргументов обратная задача заключается в оценивании величин Δx_i (или dx_i) по известной величине Δu. Для случая дифференцируемой функции одной переменной грубое решение обратной задачи тривиально: если y = f(x), то

Δy » |dy| = |f'(x)|Δx, откуда 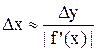. Для функции большего числа переменных обратная задача, вообще говоря, некорректна. Нужны дополнительные условия. Например, применяют принцип равных влияний, состоящий в предположении, что частные дифференциалы в (1) одинаково влияют на погрешность значения функции; тогда

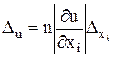, откуда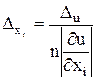

В качестве другого довольно естественного допущения можно принять равенство относительных погрешностей всех аргументов, т.е. считать 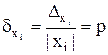при всех i = 1, 2, ..., n. Тогда 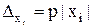и, значит, 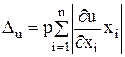. Из последнего равенства получаем величину (характеризующую относительный уровень точности задания аргументов), на основе которой за границы абсолютных погрешностей аргументов принимаем 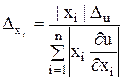. Имеются и другие, более сложные подходы к решению обратной задачи.