Поврежденной цепи линии электропередачи

Из рис. 4.7 можно найти предельное значение угла отключения КЗ, при котором устойчивая работа системы сохраняется. Оно определяется равенством площади ускорения abcd и возможной площади торможения defh. Приравнивая к нулю сумму этих площадей, получаем аналитическое выражение для предельного угла отключения КЗ [6]:

F_abcd = F_defh = 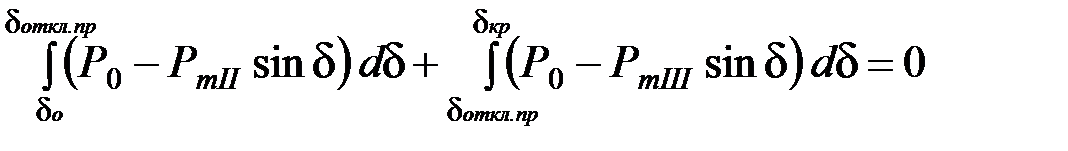. (4.6)

Раскрывая определенные интегралы, получим

cos (d_{откл. пр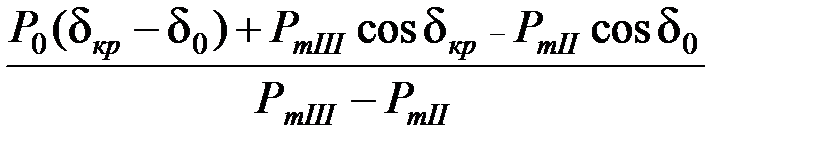}) = , (4.7)

где d_кр = p – arcsin .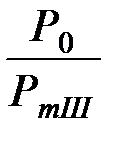

Углы выражены в радианах.

Для практических целей важнее знать не угол d_{откл.пр}, а время, за которое он будет достигнут. Для схемы рис. 4.6, а рассмотрим трехфазное КЗ в начале линии, для которого Р_mII = 0 (рис. 4.8).

Рис. 4.8. Моментно-угловая характеристика для трехфазного КЗ в начале ЛЭП

Дифференциальное уравнение движения ротора для трехфазного КЗ имеет вид

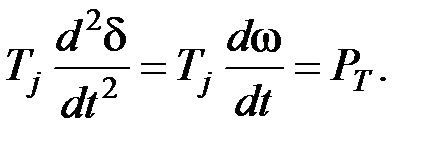(4.8)

Перепишем это уравнение в виде

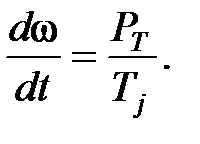(4.9)

Взяв интеграл от левой и правой частей, получим

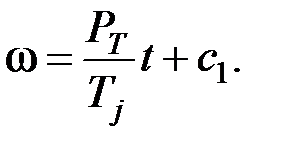(4.10)

При t = 0 относительная скорость ротора w = 0 и, следовательно, с₁ = 0.

Проинтегрировав еще раз последнее выражение, получим

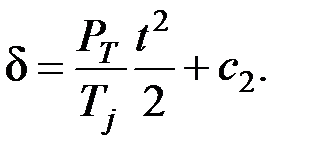(4.11)

Постоянная интегрирования с₂ определяется из условий d = d₀, с₂ = d₀ при t = 0. Окончательно зависимость угла от времени будет иметь вид

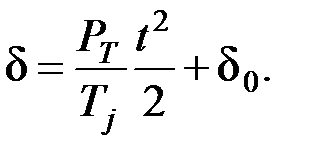(4.12)

Возрастание угла происходит по квадратичной параболе, а время, отвечающее какому-либо значению угла d, найдется из последнего выражения как

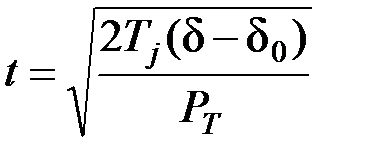. (4.13)

Предельный угол отключения трехфазного КЗ может быть определен из выражения (2.2), записанного для случая Р_mII = 0,

cos (d_{откл. пр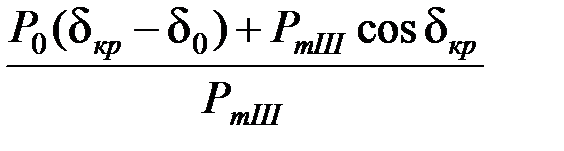}) = . (4.14)

Предельное время отключения трехфазного КЗ К⁽³⁾ определится из формулы (4.15):

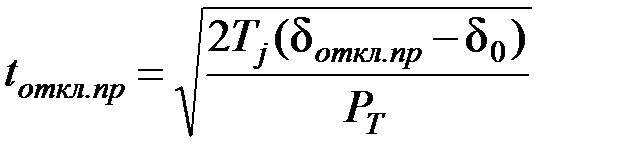. (4.15)

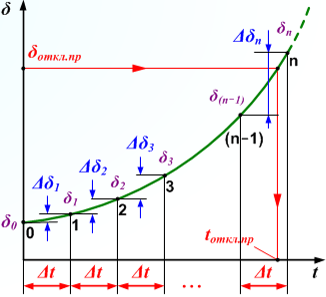Рис. 4.9. Зависимость d(t), разбитая на интервалы времени Dt

Рассмотрим случай для несимметричного КЗ Р_mII ≠ 0, тогда решение уравнения движения ротора будет представлено в виде:

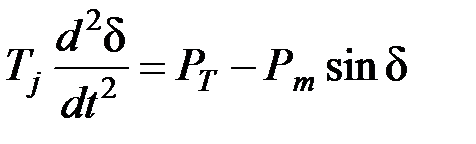. (4.16)

Такое уравнение решается методами численного интегрирования, одним из которых является метод последовательных интервалов. В соответствии с этим методом весь процесс движения ротора разбивается на ряд интервалов времени Dt и для каждого интервала последовательно вычисляется приращение угла Dd
(рис. 4.9) [1, 2, 7].

В нормальном установившемся режиме имеет место равенство
Р_Т = Р_msin(d) и угол d остается неизмененным. В момент КЗ отдаваемая генератором мощность Р_msin(d) падает, и на валу «турбина – генератор» возникает некоторый избыток мощности DР₍₀₎, и ротор машины получает ускорение

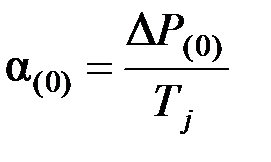. (4.17)

Здесь принято, что при небольших изменениях скорости приращения момента и мощности в относительных единицах равны между собой.

Для малого интервала времени Dt можно допустить, что избыток мощности DР₍₀₎ в течение этого интервала остается неизмененным.

Интегрируя выражение (4.16), получим в конце первого интервала

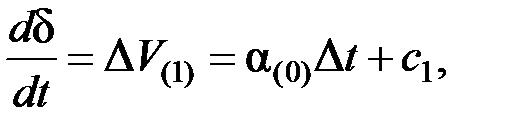d₍₁₎ = a₍₀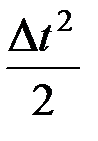₎ + с₂, (4.18)

где DV – приращение относительной скорости ротора.

Относительная скорость ротора в начальный момент КЗ равна нулю
(с₁ = 0). Относительная скорость ротора в конце первого интервала равна DV₍₁₎. При t = 0 угол d = d₀, поэтому с₂ = d₀.

Приращение угла на первом интервале с учетом (4.18) составит

Dd₍₁₎ = a₍₀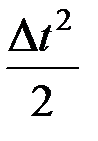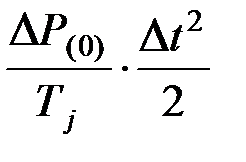₎ = . (4.19)

Здесь угол и время представлены в радианах. В практических расчетах угол выражают в градусах, а время – в секундах:

d_(град) = 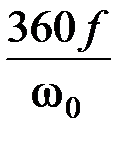d_(рад), t_(c) = 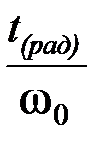, (4.20)

где w₀ – синхронная скорость.

Используя последние выражения и учитывая, что Т_j(c) = 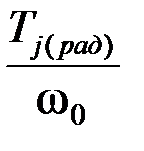, получим

d₍₁₎ = d₀ + 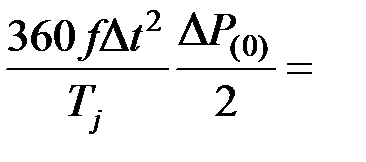d₀ + K 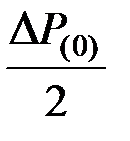, (4.21)

где К = .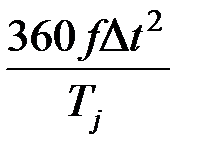

Ускорение, создаваемое во втором интервале, пропорционально избыт-ку мощности в конце первого интервала DР₍₁₎. При вычислении приращения угла в течение второго интервала необходимо учесть то, что, кроме действующего в этом интервале ускорения a₍₁₎, ротор уже имеет в начале второго интервала скорость V₍₁₎:

Dd₍₂₎ = V₍₁₎Dt + 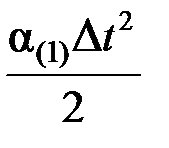= V₍₁₎Dt + К 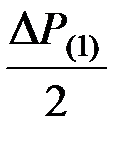, (4.22)

где DР₍₁₎ = Р₀ – Р_m sind₍₁₎.

Значение скорости V₍₁₎ неточное, так как ускорение a₍₀₎ не является постоянным в течение первого интервала времени.

По аналогии с (4.17) вычислим ускорение к концу первого интервала:

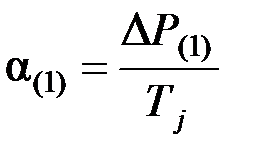, (4.23)

и предположим, что на первом интервале действует среднее ускорение

a_(0)ср = 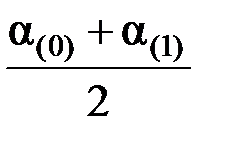. (4.24)

Тогда относительная скорость ротора будет выражена формулой

V₍₁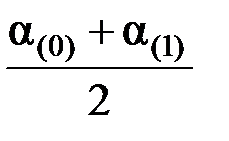₎ = Dt. (4.25)

Подставляя это уравнение в (4.22), получим

Dd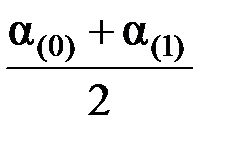₍₂₎ = Dt₂ + 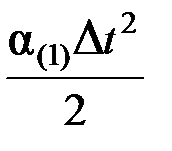= 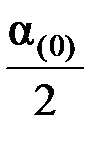Dt₂ + a₍₂₎Dt₂, (4.26)

или

Dd₍₂₎ = Dd₍₁₎ + КDР₍₁₎.

Приращение угла на последующих интервалах рассчитывается аналогично:

Dd_(n) = Dd_(n–1) + КDР_(n–1). (4.27)

Если на некотором интервале времени Dt_i происходит отключение КЗ, то избыток мощности скачкообразно меняется от некоторой величины DР¢_(i–1) до величины DР″_(i–1). Приращение угла на первом интервале после отключения КЗ определится как

Dd_(i) = Dd_(i–1) + К 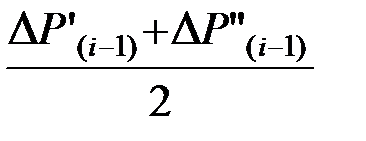. (4.28)

Расчет методом последовательных интервалов ведется до тех пор, пока угол d не начнет уменьшаться, либо не будет ясно, что этот угол неограниченно растет и динамическая устойчивость нарушается [2].

Контрольные вопросы

1. Приведите примеры больших возмущений в электроэнергетической системе.

2. Дайте определение динамической устойчивости электроэнергетической системы.

3. Дайте определение результирующей устойчивости электроэнергетической системы.

4. Назовите задачи анализа динамической устойчивости.

5. Назовите основные допущения, принимаемые при анализе динамической устойчивости.

6. Сформулируйте критерий динамической устойчивости на основе метода площадей.

7. Как определяется предельный угол отключения КЗ?

8. Как определяется предельное время отключения КЗ?

9. Запишите уравнение движения ротора синхронной машины.