Обратное интерполирование
Экстраполирование и обратное интерполирование
Пусть функция у = f(x) задана значениями в n+1 равноотстоящем узле хi = х0 + ih значениями уi =f(хi) (i = 0, 1, …, n).
| хi | х0 | х1 | х2 | … | хn |
| yi | у0 | у1 | у2 | … | уn |
Экстраполированием называется вычисление значений функции для значений аргумента, выходящих за пределы того интервала, для которого дана таблица, т.е. для значений х<х0 и х>хn.
При отыскании значений функции для х<х0 используется первый интерполяционный многочлен Ньютона. В этом случае t = < 0 и говорят, что первая интерполяционная формула Ньютона применяется для экстраполирования назад.
При отыскании значений функции для х>хn используется второй интерполяционный многочлен Ньютона.
В этом случае t = > 0 и говорят, что вторая интерполяционная формула Ньютона применяется для экстраполирования вперед.
Замечание. При экстраполировании получаются бóльшие погрешности, чем при интерполировании. Поэтому пределы его применения ограничены.
Пример. Функция y = sinx задана таблицей. Найдем значения синуса для углов х = 0,2 и х = 1
| хi | уi | Dуi | D2уi | D3уi | D4уi |
| 0,3 | 0,2955 | ||||
| 0,0939 (D у0) | |||||
| 0,4 | 0,3894 | -0,0039 (D2 у0) | |||
| 0,0900 (Dу1) | -0,0009 (D3 у0) | ||||
| 0,5 | 0,4794 | -0,0048 (D2 у1) | 0,0001 (D4 у0) | ||
| 0,0852 (Dу2) | -0,0008 (D3 у1) | ||||
| 0,6 | 0,5646 | -0,0056 (D2 у2) | -0,0001 (D4 у1) | ||
| 0,0796 (Dу3) | -0,0009 (D3 у2) | ||||
| 0,7 | 0,6442 | -0,0066 (D2 у3) | |||
| 0,0732 (Dу4) | |||||
| 0,8 | 0,7174 |
х = 0,2.
В качестве выберем х0 = 0,3 Þ t = = = -1.
Запишем первый интерполяционный многочлен третьего порядка:
у = у0 +tDу0 + D2 у0 + D3 у0 ,
Подставив численные значения, получим:
у = 0,2955 – 0,0939 + (-0,0039) + (-0,009) Þ у = 0,1986.
Можно принять sin 0,2 = 0,1986 (точное решение 0,198669).
х = 1,0.
В качестве хn выберем хn = 0,8 Þ t = = = -2.
Запишем второй интерполяционный многочлен третьего порядка:
у = уn +tDуn - 1 + D2 уn - 2 + D3 уn - 3 Þ
у = 0,7174 + 2*0,0732 + (-0,0066) + (-0,0009) Þ у = 0,8404 (точное решение 0,8414).
Обратное интерполирование
Пусть функция у = f(x) задана таблицей:
| хi | х0 | х1 | х2 | … | хn |
| yi | у0 | у1 | у2 | … | уn |
Если функция f(x) является строго монотонной (возрастающей или убывающей), то для нее существует обратная (возрастающая или убывающая) монотонная функция х = j(у).
Обратное интерполирование состоит в нахождении по промежуточному, не содержащемуся в таблице, значению функции соответствующего значения аргумента.
При обратном интерполировании находятся значения обратной функции х = j(у).
Так как табличные разности Dу данной функции не сохраняют постоянного значения (за исключением случая линейной зависимости), то для интерполирования обратной функции х = j(у) удобно применять интерполяционный многочлен Лагранжа. Интерполяционная формула в этом случае будет иметь вид:
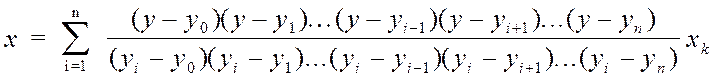 (1)
(1)
Очевидно, абсолютная погрешность обратного интерполирования может быть оценена по формуле остаточного члена интерполирования:
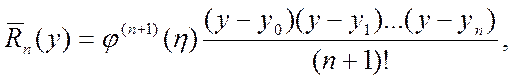 (2)
(2)
где 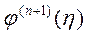 - значение производной (п+1) порядка для обратной функции. Абсолютная погрешность интерполирования
- значение производной (п+1) порядка для обратной функции. Абсолютная погрешность интерполирования
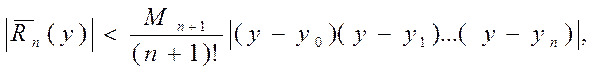
где 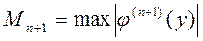 .
.
Пример. Функция задана таблицей. По заданному значению функции у=1,38 требуется найти соответствующее значение аргумента х.
| хi | 2,0 | 2,5 | 3,0 |
| yi | 1,260 | 1,35 | 1,442 |
Поменяв местами х и у, получим таблицу для обратной функции 
| хi | 1,260 | 1,35 | 1,442 |
| yi | 2,0 | 2,5 | 3,0 |
Составим многочлен Лагранжа второго порядка:
L2(x) = у0 + у1 + у2
Подставив в выражение многочлена значение хi и yi из таблицы, получим, что L2(1,38) = 2,626. Итак, φ(1,38)≈2,626.
| <== предыдущая лекция | | | следующая лекция ==> |
| Анализ финансовой устойчивости предприятия | | |
Дата добавления: 2022-07-20; просмотров: 112;










