Сравнение точности квадратурных формул.

Выше были приведены оценки абсолютной погрешности квадратурных формул:

для формул прямоугольников: |r| ;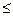

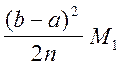для обобщенной формулы трапеции: |r| ;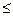

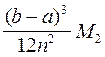для обобщенной формулы Симпсона: |r| ,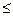

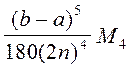где М_i= 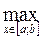|f⁽ⁱ⁾(x)| .

Сопоставление этих оценок позволяет сделать следующие выводы:

1) Т.к. производная порядка n+1 от многочлена степени n равна нулю, то получаем точно значение интеграла: по формуле трапеций, если подынтегральная функция линейна,

по формуле парабол, если подынтегральная функция – многочлен не выше третьей степени.

2) Погрешность вычислений по формулам прямоугольников обратно пропорциональна n; при использовании формулы трапеций – n²; при использовании формулы Симпсона – n⁴.

Так, например, при увеличении числа частичных отрезков в два раза погрешность вычислений по формуле прямоугольников уменьшается примерно в два раза, по формуле трапеций в 4 раза, по формуле Симпсона в 16 раз.

Для иллюстрации сделанных выводов обратимся к сравнению результатов вычисления интеграла

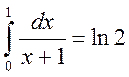
по различным квадратурным формулам. Для оценки погрешностей вычислим производные функции .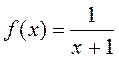

На отрезке [0; 1] все производные являются монотонными функциями. Абсолютная величина каждой из них достигает своего наибольшего значения при x=0, поэтому
М₁=1, М₂ =2, М₄=24.

Это позволяет получить при вычислении соответствующие оценки погрешностей:

по формуле прямоугольников êrú ≤ 0,05;

по формуле трапеций êrú ≤ 0,0017;

по формуле Симпсона êrú ≤ 0,000033.

Сравним полученные результаты, полученные по разным квадратурным формулам со значением ln2 0,6931472:

по формуле прямоугольников 0,71877;

по формуле трапеций 0,69377;

по формуле Симпсона 0,69315

Видно, что оценки погрешности, как и следовало, ожидать, оказались несколько завышенными.

Итак, из рассмотренных квадратурных формул наибольшую точность дает формула Симпсона, наименьшую — формула прямоугольников.