Растяжение и сжатие
2.2.1. Продольная деформация
Возьмем призматический брус с постоянной площадью поперечного сечения А, и приложенные по бокам две равные и противоположно направленные силы F, направленные по оси бруса (рис.2.11)


Рис.2.11. Продольная и поперечная деформации
Брус в продольном направлении удлиняется, а его поперечные размеры уменьшаются. Удлинение бруса будет равно 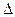 l = l1 – l,
l = l1 – l,
где 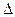 l – полное или абсолютное удлинение.
l – полное или абсолютное удлинение.
Более удобной мерой деформации является относительное удлинение (продольная деформация), определяемая по формуле:
ε = 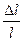 . (2.3)
. (2.3)
2.2.2. Поперечная деформация
Абсолютная поперечная деформация:
D А = А – А1. (2.4)
Относительное изменение площади поперечного сечения (поперечная деформация):
ε 0 = 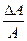 . (2.5)
. (2.5)
Опытами установлено, что даже при небольших деформациях бруса в продольном направлении его поперечные размеры изменяются.
Поперечные деформации при растяжении или сжатии пропорциональны продольной деформации и характеризуются коэффициентом Пуассона. Коэффициент Пуассона при растяжении равен:
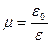 , (2.6)
, (2.6)
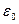 - поперечное относительное сжатие;
- поперечное относительное сжатие; 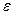 - продольное относительное удлинение.
- продольное относительное удлинение.
При сжатии:
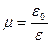 , (2.7)
, (2.7)
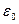 - поперечное относительное растяжение;
- поперечное относительное растяжение; 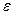 - продольное относительное сжатие.
- продольное относительное сжатие.
Для различных материалов 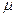 составляет от 0 до 0,5, в практических расчетах для стали принимают
составляет от 0 до 0,5, в практических расчетах для стали принимают 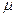 =0,32-0,35.
=0,32-0,35.
2.2.3. Закон Гука
Основной закон сопротивления материалов выражает прямую пропорциональность между нормальным напряжением и продольной деформацией:
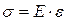 , (2.8)
, (2.8)
где Е – модуль продольной упругости (модуль Юнга), [Па]
(для стали Е = 2ּ105 МПа)
Модуль упругости характеризует жесткость материала, т.е. способность сопротивляться деформациям.
Если в законе Гука расписать продольную деформацию то получим:
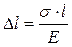 . (2.9)
. (2.9)
2.2.4. Диаграммы растяжения
Механические характеристики устанавливают границу безопасности эксплуатации элементов конструкции при статических и динамических нагрузках. К числу основных характеристик относятся: предельное напряжение, твердость, ударостойкость, вязкость, вес конструкционных материалов.
Материалы можно разделить на хрупкие и пластичные.
Пластичные обладают способностью деформироваться в широких пределах. К ним относятся: алюминиевые, медные, золотые сплавы, малоуглеродные стали. Хрупкий материал разрушается без предварительной деформации. К ним относятся: чугун, высокоуглеродные стали, металлы, керамические сплавы, стекло.
Для выполнения расчетов конструкции на прочность необходимо знать свойства материалов, из которых эти конструкции изготовлены. Наиболее распространенным испытанием материалов является испытание на растяжение. Это объясняется тем, что механические характеристики, получаемые при растяжении, позволяют судить о поведении материала при других деформациях: сжатии, сдвиге, кручении и изгибе.
Рис.2.12. Схема образца
Образец постепенно нагружается силой возрастающей от 0 до величины разрушающей образец (рис.2.12). Величина нагрузки измеряется и записывается в виде кривой зависимости между растягивающей нагрузкой и полученным удлинением.
Рассмотрим диаграмму растяжения малоуглеродистой стали (рис.2.13): в начале испытания (до отметки 1 с ординатой Nпц) удлинение Δl растет пропорционально силе F, тем самым подтверждается закон Гука. Далее удлинение Δl возрастает непропорционально силе F. При некотором значении силы (отметка 2) образец удлиняется без увеличения нагрузки. Это явление называется текучестью металла.
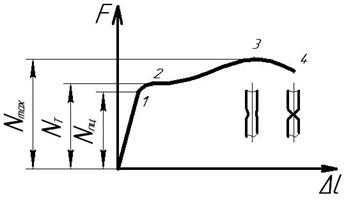
Рис.2.13.Диаграмма растяжения малоуглеродистой стали
По окончании стадии текучести, материал образца снова начинает сопротивляться нагрузке до отметки 3 с ординатой Nmax , после которой наблюдается снижение сопротивляемости образца нагрузке. Это обстоятельство объясняется тем, что на образце начинает появляться местное сужение (шейка) и в дальнейшем диаграмма фиксирует уже растяжение не всего образца, а только его участка в зоне образовавшейся шейки. Момент окончательного разрушения образца обозначается цифрой 4.
Весьма хрупким материалом является чугун. Для образца из обычного серого литейного чугуна относительное остаточное удлинение при разрыве не превышает 0,015%. При разрыве образцов из хрупких материалов шейка не образуется, и растягивающее усилие растет до момента разрушения (рис.2.14).
Деформации чугуна очень малы, они с самого начала не следуют закону Гука, а потому диаграмма получается криволинейной (кривая 1) (рис.2.14 а).
Диаграмма растяжения чугуна (кривая 2) по характеру аналогична диаграмме сжатия, но предел прочности при растяжении значительно ниже, чем предел прочности при сжатии.
Иными словами, чугун значительно хуже работает на растяжение, чем на сжатие. При сжатии чугунный образец разрушается в результате образования наклонных трещин, направленных примерно под углом 45° к оси образца (как это показано на рис.2.14 б), т. е. параллельно площадкам, в которых действуют наибольшие касательные напряжения.
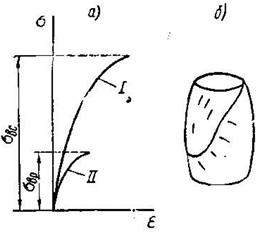
Рис.2.14 Диаграмма растяжения чугуна
Характеристики материала:
1. Отношение растягивающего усилия F1 к площади поперечного сечения А0 – предел пропорциональности.
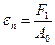 . (2.10)
. (2.10)
2. Отношение растягивающих усилий в точке 2 к первоначальному поперечному сечению стержня – предел упругости.
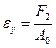 , (2.11)
, (2.11)
где 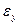 - напряжение при котором величина относительной и остаточной деформации не превышает 0,005%
- напряжение при котором величина относительной и остаточной деформации не превышает 0,005%
3. Отношение растягивающего усилия соответствующего текучести материала к площади первоначального поперечного сечения – предел текучести.
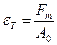 , (2.12)
, (2.12)
где 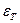 - напряжение, при котором происходит рост деформации без увеличения нагрузки.
- напряжение, при котором происходит рост деформации без увеличения нагрузки.
4. Отношение наибольшего растягивающего усилия F3 к площади первоначального сечения – предел выносливости (прочность).
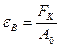 . (2.13)
. (2.13)
2.2.5. Основы прочностных расчетов элементов конструкций
Целью прочностных расчетов является: определить напряжения при фактической нагрузке, а затем сопоставить их с опасным значением.
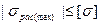 (2.14)
(2.14)
Расчеты на прочность:
1.Отношение предельного напряжения σпр к расчетному σ называется коэффициентом запаса прочности S:
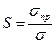 , (2.15)
, (2.15)
Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого: 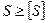
Разделив предельное напряжение на нормативный коэффициент запаса прочности, получим допускаемое напряжение 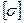 :
:
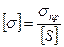 , тогда условие прочности имеет вид:
, тогда условие прочности имеет вид:
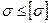 т. е. прочность элемента конструкции обеспечивается если наибольшее напряжение, возникающее в нем, не превышает допускаемого.
т. е. прочность элемента конструкции обеспечивается если наибольшее напряжение, возникающее в нем, не превышает допускаемого.
Условие прочности применительно к расчетам на прочность при растяжении (сжатии) имеет вид:
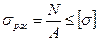 . (2.16)
. (2.16)
Для хрупких материалов допускаемое напряжение растяжения и сжатия получают исходя из предела текучести:
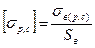 (2.17)
(2.17)
Для пластичных материалов предельным напряжением является предел текучести:
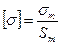 . (2.18)
. (2.18)
2.2.6. Пример расчета стержня на растяжение – сжатие
Двухступенчатый стальной брус, длины ступеней которого указаны на схеме (рис.2.15), нагружен силами F1, F2 и F3. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса l, приняв E=2•10 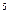 МПа. Произвести оценку прочности по участкам стержня и вычислить запас прочности, если σпр = 200 МПа, σу = 240 МПа. Числовые данные варианта взять из приложения 9, схему варианта из приложения 10.
МПа. Произвести оценку прочности по участкам стержня и вычислить запас прочности, если σпр = 200 МПа, σу = 240 МПа. Числовые данные варианта взять из приложения 9, схему варианта из приложения 10.
Схема нагружения и исходные данные
Fl= 120 кН; F2= 80 кН; F3= 80 кН; A1= 12 см2; A2= 10 см2; A3= 18 см2.
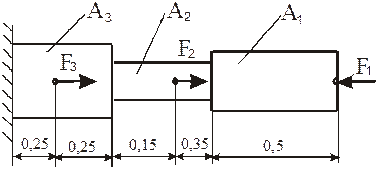
Рис. 2.15. Схема нагружения
Решение
Выделяем характерные участки стержня. Границами участков являются сечения, в которых приложены силы или изменяется площадь поперечного сечения (рис. 16). В нашем примере пять характерных участков.
Рис. 2.16. Схема нагружения с участками
Определяем продольные силы для каждого участка стержня методом сечений
1-1
∑Fix=0
- N1 – F1 = 0
N1 = - F1
N1 = - 120 кН
Рис. 3.
N1 – отрицательная, следовательно, она направлена в тело стержня.
N1= - 120 кН.
2-2 На участке 2-2 новые силы, не приложены и следовательно N2 = N1 = -120 кН.
3-3
∑Fix=0
- F1 + F2 – N3 = 0
N3 = F2 – F1 = 80 – 120 = - 40
N3 = -40 кН
4-4 N4 = -40 кН
5-5
∑Fix=0
- F1 + F2 + F3 – N5 = 0
N5 = F2 + F3 – F1= 80 + 80 – 120 = 40
N5 = 40 кН
Строим эпюру продольных сил (рис. 17).
Рис. 2.17. Схема нагружения с эпюрами
Определяем нормальные напряжения в пределах каждого характерного участка стержня:
σ1 = N1/A1 = (-120·103)/(12·102) = -100 МПа < σпр
σ2 = N2/A2 = (-120·103)/(10·102) = -120 МПа < σпр
σ3 = N3/А2 = (-40·103)/(10·102) = -40 МПа < σпр
σ4 = N4/A3 = (-40·103)/(18·102) = -25 МПа < σпр
σ 5 = N5/A3 = (40·103)/(18·102) = 25 МПа < σпр
Строим эпюру нормальных напряжений σ (рис. 2.17.)
Если σ > σ пр, то поперечное сечение стержня увеличивается и площадь его определяется по формуле:
А = N/ σ пр
Определяем коэффициент запаса прочности для второго участка стержня, на котором нормальное напряжение оказалось наибольшим.
S = σу / | σ2| = 240/120 = 2
Определяем абсолютные удлинения каждого характерного участка и подсчитываем перемещения сечений, совпадающих с границами участков:
lА= 0
lВА =lА+ΔlВА = 0 + (N5·l5)/E = 0 + (σ5·l5)/E = (25·0,25·103)/(2·105) = 0,0312 мм
lСА= lВА + ΔlСВ = lВА + (σ4·l4) /Е = 0,0312 – (25·0,25·103)/(2·105) = 0
lда = lСА + ΔlДС = lСА + (бз·lз)/Е = 0 – (40·0,15·103)/(2·105) = - 0,03 мм
lЕА = lДА + (б2×l2)/Е = - 0,03 – (120·0,35·103)/ (2·105) = - 0,24 мм
lКА = lЕА +(б1×l1)/Е = = - 0,24 – (100·0,5·103)/(2·105) = -0,49 мм.
Строим эпюру абсолютных удлинений (рис. 17).
Сдвиг
2.3.1. Чистый сдвиг. Закон Гука при сдвиге
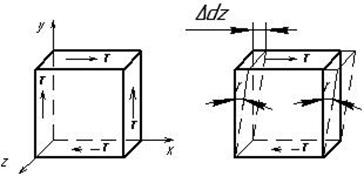
Рис. 2.18. Чистый сдвиг
При чистом сдвиге на четырех гранях выделенного элемента возникают только касательные напряжения, а две грани свободны от напряжений (рис.2.18).
Явление сдвига состоит в том, что под действием внешних сил первоначальная форма выделенного элемента искажается, например, горизонтальные площадки сдвигаются относительно друг друга на расстояние Δdz, называемое абсолютным сдвигом, и угол 90 градусов между смежными площадками изменяется на величину γ. Этот угол называется углом сдвига или угловой деформацией.
Установлено, что касательные напряжения и угол сдвига в пределах упругих деформаций связаны между собой прямой пропорциональной зависимостью:
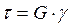 , которая называется законом Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига и характеризует жесткость материала при сдвиге.
, которая называется законом Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига и характеризует жесткость материала при сдвиге.
Между модулем упругости Е, модулем сдвига G и коэффициентом Пуассона μ существует зависимость:
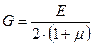 . (2.19)
. (2.19)
2.3.2. Расчет на сдвиг (срез)
Если два бруса соединить между собой штифтом, а затем нагрузить направленными в противоположные сторонами силами F, то при значительных силах или небольшом диаметре штифта, он может быть разрушен по сечению, расположенному в плоскости соприкасания поверхностей соединяемых брусьев. Такое разрушение соединительных деталей (штифта, болта, заклепки, шпонки), происходящее под действием нагрузок, перпендикулярных их собственным осям (поперечные нагрузки), называется срезом(рис.2.19).
Условие прочности при расчете на срез имеет вид:
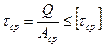 , (2.20)
, (2.20)
где 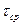 - расчетное напряжение среза в поперечном сечении детали;
- расчетное напряжение среза в поперечном сечении детали; 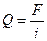 - поперечная сила, возникающая в этом сечении;
- поперечная сила, возникающая в этом сечении; 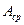 - площадь поперечного сечения срезаемой детали (площадь среза); I - число соединительных деталей.
- площадь поперечного сечения срезаемой детали (площадь среза); I - число соединительных деталей.
При расчете болтов, штифтов, шпонок и прочего принимают: 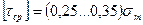 или
или 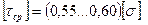
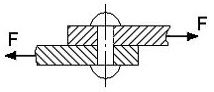
Рис.2.19. Срез
Кручение
2.4.1. Общие сведения о деформации кручения
Наглядное представление о деформации кручения дает действие двух равных и противоположно направленных крутящих моментов (рис.2.20).


Рис.2.20.Деформация кручения
В результате деформации образующие вала получают вид винтовых линий. Такой вид получают образующие валы и в случае следующего закрепления (рис.2.21).
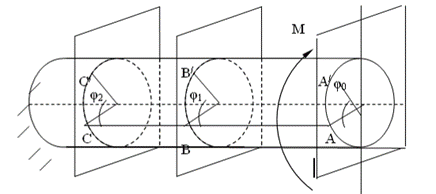
Рис. 2.21. Деформация вала
При действии крутящего момента М все линии рассматриваемой образующей будут отклоняться от первоначального положения на некоторые углы по окружности. На основе этого можно сделать выводы:
1. При кручении, в каждом сечении вала происходит поворот точек по окружности относительно оси. Следовательно, вал испытывает кручение, если к нему прикладывается пара сил направленных перпендикулярно осям.
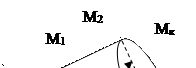 2. Под действием внешних моментов, в поперечном сечении вала, возникает единственная составляющая главного момента, а именно крутящий момент Мк (рис. 2.22).
2. Под действием внешних моментов, в поперечном сечении вала, возникает единственная составляющая главного момента, а именно крутящий момент Мк (рис. 2.22).

Рис.2.22. Главный момент
3. Деформация кручения вала заключается в повороте поперечных сечений относительно друг друга, при этом углы поворота прямопропорциональны растяжению.
4. Угол поворота рассматриваемого сечения равен углу закручивания части вала, которая заключена между данным сечением и заделкой. Угол кольцевого сечения называется углом закручивания вала.
5. В произвольном сечении угол поворота можно оценить относительным углом закручивания:
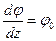
где 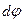 - угол закручивания выделенного элемента;
- угол закручивания выделенного элемента; 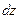 - расстояние от рассматриваемого сечения до заделки,
- расстояние от рассматриваемого сечения до заделки, 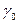 - относительный угол закручивания.
- относительный угол закручивания.
Если балка длиной l м имеет постоянное поперечное сечение и нагружена внешним моментом на конце вала, то относительный угол закручивания будет:
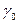 = const
= const
6. При кручении вала возникает деформация сдвига между соседними сечениями, следовательно, при кручении поперечных сечений валов, возникают только касательные внутренние силы создающие крутящий момент.
Крутящие моменты в поперечных сечениях вала определяют методом сечений. При использовании уравнений равновесия:
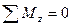 ;
; 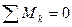
Крутящий момент в поперечном сечении вала численно равен алгебраической сумме внешних моментов, которые приложены к оставленной для рассмотрения части вала.
 Считаем крутящий момент положительным, если внешний момент по отношению к рассматриваемой части вала направлен по ходу часовой стрелки (рис.23).
Считаем крутящий момент положительным, если внешний момент по отношению к рассматриваемой части вала направлен по ходу часовой стрелки (рис.23).
Рис.2.23. Правило знаков
Эпюра крутящих моментов представляет собой график изменения крутящего момента по длине вала. С помощью эпюры крутящих моментов определяют опасное сечение вала, то есть такое в котором действует наибольший крутящий момент.
2.4.2. Напряжение и деформация при кручении
В поперечных сечениях скрученного вала (рис.2.24) действует, только касательное напряжение 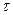 , следовательно, крутящий момент представляет собой результирующий момент внутренних касательных сил, то есть действующий на бесконечно малых площадках поперечного сечения, его можно выразить:
, следовательно, крутящий момент представляет собой результирующий момент внутренних касательных сил, то есть действующий на бесконечно малых площадках поперечного сечения, его можно выразить:
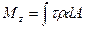 .
.
где 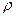 - расстояние или плечо элементарной силы относительно продольной оси вала;
- расстояние или плечо элементарной силы относительно продольной оси вала;
r –радиус вала.
 Данная зависимость отражает статическую сторону работы сечения, но не позволяет определить значение касательных напряжений по известному крутящему моменту, так как в данном случае не установлен закон распределения касательных напряжений по сечению.
Данная зависимость отражает статическую сторону работы сечения, но не позволяет определить значение касательных напряжений по известному крутящему моменту, так как в данном случае не установлен закон распределения касательных напряжений по сечению.
Рис. 2.24. Схема скрученного вала
Угол сдвига для некоторого поперечного сечения.
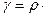 φ0
φ0
где φ0 – угол поворота.
Тогда касательное напряжение прямо пропорционально расстоянию до оси вала.
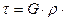 φ0. (2.21)
φ0. (2.21)
Эпюра распределения 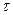 вдоль радиуса сечения вала всегда имеет вид треугольника, если соблюдаются выше перечисленные условия (рис. 2.25). Если вал состоит из одного участка (то есть имеет постоянное сечение и постоянный по длине крутящий момент), то
вдоль радиуса сечения вала всегда имеет вид треугольника, если соблюдаются выше перечисленные условия (рис. 2.25). Если вал состоит из одного участка (то есть имеет постоянное сечение и постоянный по длине крутящий момент), то 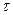 в данном волокне бруса будет постоянным по всей длине участка.
в данном волокне бруса будет постоянным по всей длине участка.

Рис. 2.25. Эпюра касательных напряжений 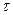
2.4.3. Расчет на жесткость и прочность при кручении
1. Прочность 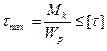 , (2.22)
, (2.22)
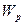 - полярный момент сопротивления [
- полярный момент сопротивления [ 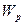 ] = [м3]
] = [м3]
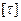 - допускаемое касательное напряжение, устанавливается в зависимости от допускаемого напряжения при растяжении.
- допускаемое касательное напряжение, устанавливается в зависимости от допускаемого напряжения при растяжении.
2. Условие жесткости бруса при кручении состоит в том, чтобы относительный угол закручивания φ0 не превосходил некоторого заданного допускаемого значения [φ0]
φ0 ≤ [φ] – условие жесткости; (2.23)
где φ0 – относительный угол закручивания;
[φ] – допускаемый относительный угол закручивания.
φ0 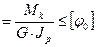 ; [φ0] = 0,2…1; [
; [φ0] = 0,2…1; [ 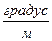 ] (2.24)
] (2.24)
2.4.4. Пример расчета вала при кручении
Для стального трансмиссионного вала (рис. 2.26) G = 8·1010 МПа:
1. Определите значение скручивающих моментов (подводимого к шкиву 0 и снимаемых со шкивов 1, 2, 3).
2. Постройте эпюры крутящих моментов.
3. Определите диаметры каждого участка ступенчатого вала из условия прочности. Окончательно принимаемые значения должны быть округлены до ближайших стандартных по ГОСТ 6636-69. Диаметр вала (мм): 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200.
4. Вычертите в масштабе эскиз ступенчатого вала.
5. Постройте эпюру углов закручивания относительно левого шкива на валу.
6. Проверьте жесткость вала при кручении и при недостаточной жесткости участков вала, определите их диаметры из условий жесткости.
Числовые данные варианта взять из приложения 11, схему варианта из приложения 12.
Схема нагружения и исходные данные.
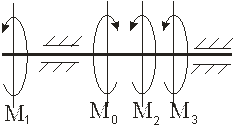
Рис. 2.26. Схема нагружения
ИСХОДНЫЕ ДАННЫЕ
| а | Р0 | Р1 | Р2 | Р3 | ω | [τ] | [φ] |
| м | кВт | рад/с | мПа | рад/м | |||
| 0,1 | 0,02 |
Рис. 2.27. Расчетная схема и результаты расчетов
Решение
1. Определяем внешние скручивающие моменты:
М0 = 103 Ро/ω = 103 90/75 = 1200 Н·м
М1 = 103 Р1/ω = 103 50/75 = 666,7 Н·м
М2 = 103 Р2/ω = 103 20/75 = 266,7 Н·м
М3 = 103 Р3/ω = 103 20/75 = 266,7 Н·м
2. Разбиваем вал на характерные участки (рис. 2.27.).
Их границами являются сечения, в которых приложены внешние крутящие моменты М на каждом участке вала. Для этого воспользуемся методом сечений:
1-1: Мк1 = - М1 = - 666,7 Н·м
2-2: Мк2 = - М1+ М0 = - 666,7 + 1200 = 533,3 Н·м
3-3: Мк3= - М1+ М0 – М2 = 266,6 Н·м
Строим эпюру крутящих моментов.
3. Определяем диаметры на каждом участке вала, если из условия прочности:
d = 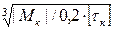 .
.
I: d1 = 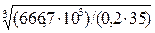 =
= 
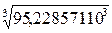 = 45,6 мм.
= 45,6 мм.
Принимаем d1 = 50 мм.
II: d2 = 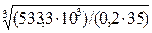 =
= 
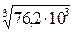 = 42,3 мм.
= 42,3 мм.
Принимаем d2 = 45 мм.
III: d3 = 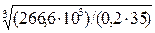 =
= 
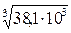 = 33,6 мм.
= 33,6 мм.
Принимаем d3 = 35 мм.
На участке IV диаметр вала принимаем конструктивно d4 =20 мм. Вычерчиваем эскиз вала в соответствии с принятыми значениями диаметров ступеней.
4. Для определения углов закручивания вала предварительно вычисляем полярные моменты инерции (Iр, м4) отдельных сечений вала.
Ipl = π d14/32 = 3,14·(5,0·10-2)4/32 = 61,3·10-8 м4
Ip2 = π d24/32 = 3,14· (4,5·10-2)4/32 = 40,2·10-8 м4
Ip3 = π d34/32 = 3,14· (3,0·10-2)4/32 = 7,9 ·10-8 м4
5. Относительные углы закручивания (φ, град/м) на отдельных участках вала:
φ = Мк / G · Ip.
φ1 = Мк1 / G · Ip1 = 666,7/8·1010·61,3·10-8 = 666,7·10-2/490,4 = 0,013 рад/м.
|φ1| < [φ].
φ2 = Мк2 / G · Ip2 = 533,3/8·1010·40,2·10-8 = 533,3·10-2/321,6 = 0,017 рад/м.
|φ2| < [φ].
φ3 = Мк3 / G · Ip3 = 266,6/8·1010·7,9·10-8 = 266,6·10-2/63,2 = 0,042 рад/м.
|φ2| > [φ].
Следовательно на участке 3-3 жесткость вала не обеспечена.
Вычислим диаметр вала на участке 3-3 из условий жесткости, определив предварительно для этого значение полярного момента инерции Ip3.
Ip3 = Мк3/G·[φ] = 266,6/8·1010·0,02 = 266,6/0,16·1010 = 16,67·10-8 м4
d3 = 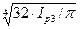 =
= 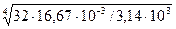 =36,1 мм
=36,1 мм
Принимаем d3 = 40 мм.
Изгиб
2.5.1. Общие сведения
При изгибе характерно: а) у рассматриваемого бруса имеется хотя бы одна плоскость симметрии, б) плоскость действия всех нагрузок (включая реакции опор) совпадает с плоскостью симметрии бруса (рис.2.28). Брус, работающий на изгиб называется балкой. При изгибе в балке существует нейтральная линия – это слой волокон, которые не изменяют своей первоначальной длины – нейтральный слой (рис.2.29).

Рис. 2.28. Схема бруса

Рис.2.29. Изгиб балки
2.5.2. Понятие об изгибающем моменте и поперечной силе
К балке приложены две равные и противоположно направленные по знаку силы (М) (рис.2.30). Рассматривая равновесие, части балки, приложенной слева или справа от сечения n-n, видим, что во всех поперечных сечениях возникает только изгибающий момент, при этом Ми = М – это случай чистого изгиба.

Рис. 2.30.Изгибающий момент
m – приложенный активный момент (внешняя нагрузка); Ми – изгибающий момент.
К балке приложены активные и реактивные силы перпендикулярные к ее оси (рис.2.31). Рассмотрим равновесие частей балки расположенных справа и слева от поперечного сечения. В них действует изгибающий момент и поперечные силы, следовательно, в рассматриваемом случае в точках поперечного сечения действует два вида напряжений:
· Нормальное напряжение – вызывает изгибающий момент.
· Касательное напряжение – соответствует поперечной силе, то есть Q.
В данном случае поперечная сила Q является равнодействующей, внутренних касательных сил в поперечных сечениях и имеет противоположное направление для левой и правой частей балки. Изгибающий момент в сечение балки, численно равен алгебраической сумме моментов относительно центра тяжести сечения. Поперечные силы в сечение балки численно равны алгебраической сумме всех внешних сил действующих справа (слева) от сечения.

Рис. 2.31. Изгибающий момент и поперечная сила
2.5.3. Правило знаков
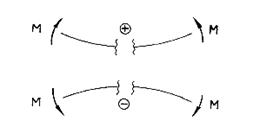
Рис . 2.32.Правило знаков для момента
Если внешняя нагрузка стремиться изогнуть балку выпуклостью вниз, то - знак плюс, и наоборот, если выпуклостью вверх то - знак минус (рис. 2.32).
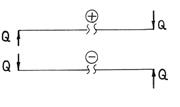
Рис. 2.33.Правило знаков для поперечной силы
Считаем поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной – в противном случае (рис. 2.33).
2.5.4. Эпюры поперечных сил и изгибающих моментов
Для наглядного распределения вдоль оси балки поперечных сил и изгибающих моментов строят соответствующие эпюры. Они дают возможность:
· Определить наличие опасных сечений по длине балки.
· Установить значения поперечных сил и изгибающих моментов в этих опасных сечениях.
При построении эпюр Q и М рекомендуется придерживаться такой последовательности:
1) Найти опорные реакции (для консольной балки их можно не находить)
2) Разбить брус на характерные участки.
3) Применяя метод сечений построить эпюру поперечных сил. Если поперечная сила, изменяясь непрерывно, проходит через нулевое значение, то необходимо определить абсциссу сечения, где Q обращается в ноль.
4) Вычислить в характерных сечениях значения изгибающих моментов и по найденным ординатам построить эпюру М.
2.5.5. Осевой момент инерции
Известно, что при изгибе во всех точках поперечного сечения балки возникают напряжения. В общем случае это нормальное и касательное напряжения. При чистом изгибе только нормальное напряжение, оно зависит от нагрузки и геометрии сечения.

Рис. 2.34. Нейтральная ось.
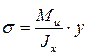 , (2.25)
, (2.25)
где 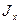 -осевой момент инерции;
-осевой момент инерции;
у – расстояние от рассматриваемого слоя до нейтральной оси (рис. 2.34).
В этой формуле при Ми и 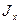 величина у переменная, поэтому нормальное напряжение по сечению линейно зависит от расстояния у.
величина у переменная, поэтому нормальное напряжение по сечению линейно зависит от расстояния у.
Осевые моменты инерции простейших сечений (рис. 2.35):
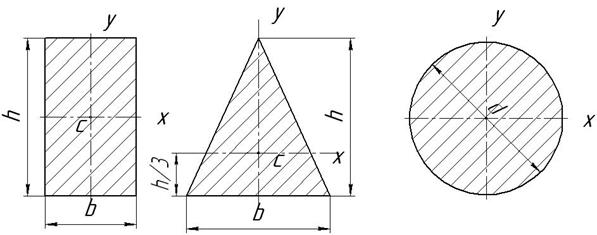
Рис. 2.35. Осевые моменты инерции
1) Прямоугольник
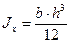 ;
; 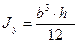 ; (2.26)
; (2.26)
2) Треугольник равнобедренный
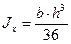 ,
, 
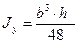 ; (2.27)
; (2.27)
3) Круг
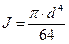 . (2.28)
. (2.28)
Условие прочности при изгибе по нормальному напряжению:
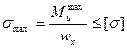 (2.29)
(2.29)
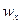 - осевой момент сопротивления.
- осевой момент сопротивления.
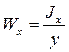 , [м3] (2.30)
, [м3] (2.30)
При решении трех задач выполняется три вида расчетов:
· Проверка прочности балок по нормальным напряжениям (проверочный расчет).
· Подбор поперечного сечения балки (проектный расчет).
· Определение максимальной нагрузки на балку.
2.5.6. Линейные и угловые перемещения при изгибе.
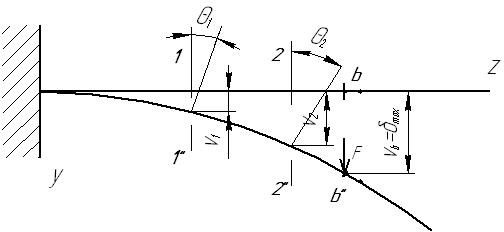
Рис. 2.36.Схема линейных и угловых перемещений при изгибе
При изгибе под действием поперечных нагрузок продольная ось бруса (балки) искривляется. Если изгиб протекает в пределах упругих свойств материала, т.е. в пределах закона Гука, то после снятия нагрузок ось бруса снова выпрямляется. Поэтому изогнутую ось бруса называют упругой линией. По форме, которую при нагружении бруса принимает его упругая линия, можно судить об угловых и линейных перемещениях при изгибе.
Изобразим продольную ось балки, защемленной одним концом. Под действием нагрузки F, перпендикулярной оси балки и расположенной в главной плоскости, ось, оставаясь в этой плоскости изгибается и принимает вид отрезка кривой (рис. 2.36).
При этом центры тяжести произвольных сечений 1 и 2 при изгибе балки переместились соответственно на расстояния v1 и v2, а сами сечения, оставаясь плоскими (по гипотезе плоских сечений), повернулись на углы θ1 и θ2, которые равны углу между касательной к изогнутой оси в данной точке и направлением оси недеформированного бруса.
Линейные перемещения центров тяжести произвольных поперечных сечений при изгибе называются прогибами бруса, а наибольший прогиб называется стрелой прогиба.
Угол поворота определяется по формуле:
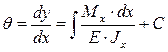 , (2.31)
, (2.31)
Прогиб по формуле:
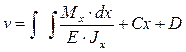 . (2.32)
. (2.32)
Решения по данным уравнениям очень громоздки, поэтому чаще используют более рациональный способ определения прогиба с помощью интеграла Мора:
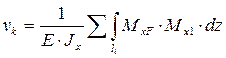 , (2.33)
, (2.33)
где MxF – уравнение изгибающего момента от нагрузки F, Mx1 - уравнение изгибающего момента от единичной силы.
Угол поворота определяется по аналогичной формуле, только в этом случае Mx1 – уравнение изгибающего момента от единичного момента.
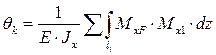 (2.34)
(2.34)
Расчет балок на жесткость:
Многие элементы строительных и машиностроительных конструкций требуют расчета на жесткость. Условие жесткости обычно выражается неравенством:
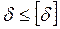 , суть, которого в том, что максимальный прогиб не должен превышать допускаемого значения.
, суть, которого в том, что максимальный прогиб не должен превышать допускаемого значения.
Для облегчения расчетов на жесткость приведем формулы прогибов и углов поворота сечений балок в простейших случаях их нагружения (рис.2.37).
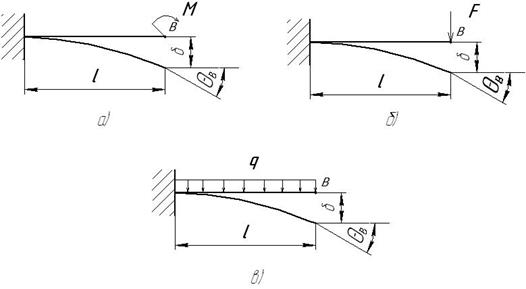
Рис. 2.37. Простейшие случаи нагружения балок
а) 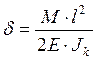 ,
, 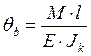 (2.35)
(2.35)
б) 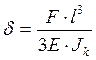 ,
, 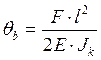 (2.36)
(2.36)
в) 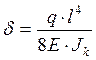 ,
, 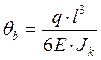 (2.37)
(2.37)
2.5.7. Пример расчета балки на изгиб
Для заданной балки (рис. 2.38.):
1. Постройте эпюры Q, Ми.
2. Подберите круглое поперечное сечение балки.
Числовые данные варианта взять из приложения 13, схему варианта из приложения 14.
Исходные данные
| а | q | F | M | [σ] |
| м | КН/м | кН | кН·м | МПа |
Схема нагружения и результаты.
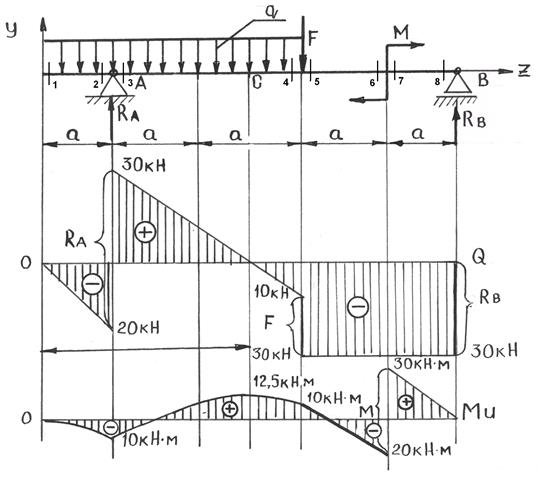
Рис. 2.38. Схема нагружения и эпюры.
1) Определим опорные реакции, для чего составим два уравнения моментов:
Σ МА=0 q·a·0,5a – q·2a·a – F·2a – M + RB·4а = 0
20·1·0,5-20·2·1 – 20·2 – 50+4·RB = 0
Σ МВ=0 q·3a·3,5a – RA·4a + F·2a – M = 0
20·3·3,5 – RA·4 + 20·2 – 50 = 0
Откуда RB = 120/4 = 30 кН
RA = 200/4 = 50 кH
Для проверки правильности определения опорных реакций составляем сумму проекций всех сил, приложенных к балке на вертикальную ось Y:
Σ Fiy = 0 -q·3а + RA – F + RB = 0
-20·3 + 30 – 20 + 50 = 0
2) Намечаем характерные сечения:
К характерным сечениям относятся:
а) сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;
б) сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;
в) сечения, расположенные бесконечно близко к опорам, а также на свободных концах.
3) Вычисляем значения поперечных сил в характерных сечениях:
Рассматриваем левую отсеченную часть:
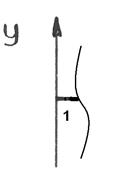
1:1 Qу1=0
Мх1=0
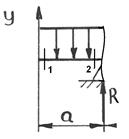
2:2 Qу2=-q·а=-20·1= -20 кН
Мх2=-q·а·0,5а=-20·0,5= -10 кН
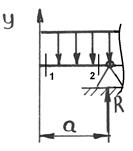
3:3 Qу3=-q·а+RАу=-20·1+50=30 кН
Мх3=-q·а·0,5а=-20·0,5=-10 кН
4:4 Qу4=-q·3а+RАу=-20·3+50=-10 кН
Мх4=-q·3а·1,5а+RАу·2а=10 кН
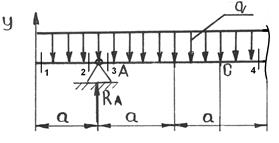
Для сечений 5-8 удобнее рассматривать правую отсеченную часть:
5:5 Qу5=-RВу=-30 кН
Мх5=-М+
Дата добавления: 2022-05-27; просмотров: 184;










