Внутренние силы. Метод сечений

Рассмотрим тело произвольной формы в “спокойном”, ненагруженном состоянии. Между его частицами всегда существуют силы взаимодействия, которые стремятся сохранить его как единое целое, то есть препятствуют изменению взаимного расположения частиц. При нагружении тела произвольной внешней нагрузкой силы взаимодействия между частицами изменяются, появляются дополнительные силы взаимодействия, которые приводят к изменению взаимного расположения частиц тела, то есть к его деформации.

Эти дополнительные силы взаимодействия называются внутренними силами упругости (ВСУ) и являются предметом изучения сопротивления материалов.

Анализ характера распределения внутренних сил упругости осуществляется при помощи метода сечений. Это метод, позволяющий выявить внутренние усилия в сечении стержня, перевести их в разряд внешних сил и определить их численные значения.

Рассмотрим тело произвольной формы, нагруженное самоуравновешенной системой сил (рис. 2.6,а). В интересующем нас сечении мысленно рассечем его плоскостью на две части (рис. 2.6,б).

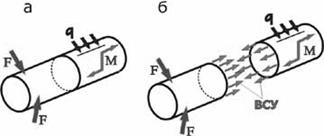
Рис.2.6. Тело, нагруженное самоуравновешенной системой сил

Внутренние силы упругости определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения. В разных сечениях тела возникают разные внутренние силы упругости, но по принципу действия и противодействия они всегда взаимны. Правая отсеченная часть тела действует на левую точно так же, как и левая, на правую, а это означает, что равнодействующая внутренних сил может определяться из условий равновесия, как левой отсеченной части тела, так и правой.

Из курса теоретической механики известно, что любую произвольную систему сил можно привести к центру тяжести сечения. В результате внутренние силы упругости, действующие в рассматриваемом сечении, приводятся к главному вектору R и главному моменту M. Выберем прямоугольную систему координат OXYZ так, что ось Z будет направлена по нормали к поперечному сечению, а оси X и Y лежат в плоскости сечения. Проецируя главный вектор R на каждую из осей, а главный момент M на каждую из координатных плоскостей, получим шесть величин: 3 силы и 3 момента, которые называются внутренними силовыми факторами (рис.2.7).

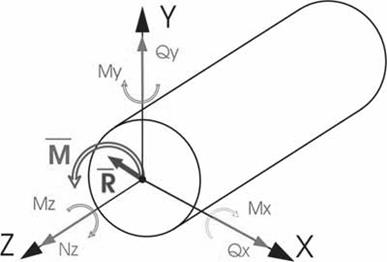
Рис.2.7 Схема внутренних силовых факторов

Полученные таким образом шесть внутренних силовых факторов (ВСФ) имеют строго определенные названия:

N_z – продольная (нормальная) сила;

Q_x, Q_y – поперечные (перерезывающие) силы;

M_x, M_y – изгибающие моменты;

M_z – крутящий момент.

Иногда обозначение M_z заменяют на M_кр или M_к, более точно отвечающие физическому смыслу этой величины.

График, показывающий, как меняется внутренний силовой фактор по длине рассматриваемого тела, называется эпюрой.

Если внешние силы заданы, то внутренние силовые факторы вычисляются на основании условия равновесия, как алгебраические суммы проекций сил и моментов, действующих на мысленно отсеченную часть тела.

Правильность построения эпюры обеспечивается, в первую очередь, надлежащим выбором характерных сечений, то есть тех сечений, в которых величина внутреннего силового фактора обязательно должна быть определена.

К характерным сечениям относятся:

1) сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;

2) сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;

3) сечения, расположенные бесконечно близко к опорам, а также на свободных концах.

Виды сопротивлений

В зависимости от характера внешней нагрузки и от особенностей нагружаемого тела, в поперечных сечениях могут возникать не все шесть внутренних силовых факторов, а какой-либо один или некоторая их комбинация. В соответствии с этим различают следующие виды сопротивлений:

Растяжение (или сжатие) – это вид сопротивления, при котором во всех поперечных сечениях возникает только продольная сила Nz.

Кручение – это вид сопротивления, при котором во всех поперечных сечениях возникает только крутящий момент M_кр.

Чистый изгиб – это вид сопротивления, при котором во всех поперечных сечениях возникает только изгибающий момент M_x (или M_y). Чаще всего изгибающий момент M_x сопровождается наличием поперечной силы Q_y(или момент M_y сопровождается наличием поперечной силы Q_x). В этом случае имеет место поперечный изгиб.

Возможны случаи, когда в поперечных сечениях возникают два и более внутренних силовых фактора одновременно (исключая их комбинации, рассмотренные выше), тогда говорят о сложном сопротивлении.

Все перечисленные виды сопротивлений будут подробно рассмотрены в дальнейших разделах курса.

2.1.7. Напряжения и деформации

Напряжение – это числовая мера интенсивности внутренних сил.

Если известно, что внутренние силы распределяются по сечению напряженного тела равномерно, то в этом случае (рис.2.8):

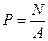, (2.1)

P- напряжение (внутреннее), Па

N – суммарная сила упругости, Н

A- площадь сечения, мм²

В общем случае напряжение P на данной площадке dA будет составлять с этой площадкой некоторый угол α.

Нормальное напряжение 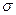направленно перпендикулярно к площадке, а касательное 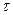по касательной к сечению.

Рис.2.8. Внутренниенапряжения

Рассечем брус, находящийся под действием внешних сил, на две части поперечным сечением, отбросим правую часть и приложим для равновесия внутренние силы (рис.2.9).

Рис.2.9. Схема бруса.

Равнодействующая сила упругости будет действовать по оси бруса и по величине равна N.

Воспользуемся гипотезой плоских сечений: в рассматриваем брусе, все плоские сечения нормальные к оси бруса остаются, и после деформации плоскими и нормальными к оси. Поэтому напряжение во всех точках поперечного сечения будет определяться по формуле:

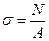. (2.2)

Наличие нормального напряжения σ в любой точке поперечного сечения обусловлено возникновением в этом сечении нормальной силы N или изгибающих моментов М_x и М_y. Наличие касательных напряжений τ обусловлено внутренними силовыми факторами, возникающими в плоскости сечения, т.е. поперечными силами Q_x и Q_y или крутящим моментом.

При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.

Отнесем недеформированное тело к декартовой системе координат Oxyz (рис. 2.10). Положение некоторой точки М в этой системе координат определяется радиус-вектором r (х, у, z). В деформированном состоянии точка М займет новое положение М^/, характеризуемое радиус-вектором r' (х, у, z). Вектор u=r'—r называется вектором полных перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и (х, у, z), v (х, у, z), w (х, у, z).

Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткое целое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.

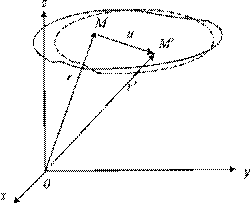
Рис.2.10 Композиция вектора перемещения