Псевдобулевы функции

Пусть Р — произвольное поле. Элементы 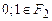будем рассматривать как нуль и единицу поля .

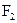Определение 4.1. Псевдобулевой функцией от 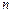переменных, или 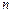-местной псевдобулевой функцией, над полем Р при 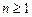называется любое отображение 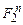в Р. Нуль-местными псевдобулевыми функциями над Р называются все элементы поля Р.

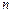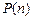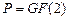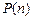Множество всех пседобулевых функций от переменных над полем Р обозначим через . В частности, при класс совпадает с классом булевых функций 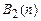. В других случаях эти классы различны, и если условиться псевдобулеву функцию со значением из 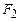считать булевой, то 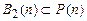. Множество функций 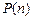относительно естественным образом определяемых операций сложения функций и умножения функций на элементы из Р образуют линейное пространство над полем Р.

Рассмотрим систему функций:

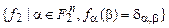, (4.1)

где 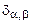— символ Кронекера, т.е.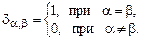

Утверждение 4.2. Система функций (4.1) является базисом пространства .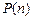

Доказательство. Очевидно, что система (4.1) — линейно независимая система. Далее пусть 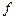— произвольная функция из 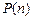. Тогда очевидно, что

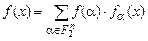. (4.2)

Отсюда следует, что (4.1) — базис пространства .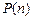

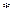
Замечание 4.3. Если 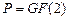, то 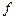— булева функция и разложение (4.2) функции 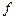совпадает с разложением, полученным заменой в её СДНФ операции 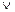на .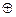

Замечание 4.4. Если 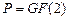, то система функций

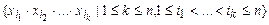(4.3)

является базисом пространства 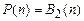. Это следует из теоремы 2.15 об однозначном представлении булевых функций многочленами Жегалкина. В этом случае представление функции многочленом Жегалкина есть (4.3).

Замечание 4.5. Представление булевых функций через базисы пространства 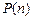сопряжено со многими трудностями. Вот две из них:

непростым является вопрос об описании базисов пространства ;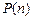

если даже имеется система функций, являющаяся базисом пространства, то в общем случае сложным является вопрос о нахождении коэффициентов в разложении булевой функции по указанному базису.

Замечание 4.6. В решении вопроса об описании базисов пространства 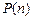иногда оказывается полезным переход от пространства 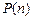к пространству 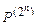векторов-столбцов длины 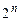над полем Р. Сопоставим каждой функции 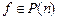вектор столбец значений 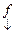этой функции. В итоге получаем отображение 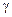пространства 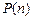в пространство 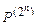. Нетрудно видеть, что 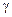есть изоморфизм пространств, а поэтому система функций 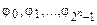является базисом пространства 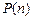тогда и только тогда, когда матрица 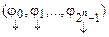является невырожденной.

4.2. Функции k-значной логики

Пусть 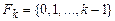, где .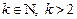

Определение 4.7. Функцией k-значной логики, или k-значной функцией, от переменных при 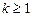называется произвольное отображение 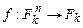, k-значными функциями от 0 переменных называются функции-константы 0, 1, …, k – 1.

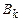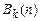Обозначим через и множества всех k-значных функций и k-значных функций от 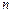переменных.

При изучении k-значных функций используются многие из терминов и обозначений, введенных при изучении булевых функций. В частности, аналогичным образом определяются равенство функций, существенные и несущественные переменные, функции от 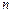переменных, тождественно равны константам 0, 1, …, k – 1, подфункции и т.д.

Так как множество 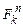конечно, то k-значную функцию от 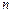переменных можно задать таблицей её значений на всех наборах (или векторах) из 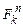. При этом условимся записывать их в порядке возрастания как числа в конечной системе исчисления. Непосредственно из табличного значения видно, что различных k-значных функций равно 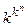. При 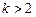табличное задание k-значных функций практически еще более трудно осуществимо.

В связи с этим важным вопросом является вопрос о разработке аналитических способов k-значных функций.

Множество 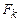можно рассматривать как кольцо вычетов 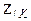по модулю 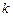, и потому можно считать определенными на 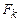операции сложения и умножения по модулю 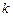. Будем обозначать эти операции при 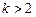теми же значками 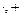, что и операции над числами. Используя эти операции и функции-константы можно построить кольцо многочленов 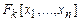от переменных 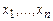. Каждый многочлен из этого кольца представляет k-значную функцию от 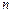переменных. При простом 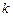, когда 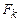есть поле, многочленами представляются все k-значные функции. При составном 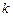— это не так.

Используя операции сложения и умножения, а также элементарные функции

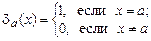
можно получить представление k-значной функции, сходное с совершенной дизъюнктивной нормальной формой для случая :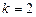

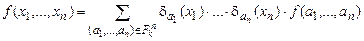. (4.4)

Другими, часто используемыми операциями на 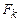являются аналоги дизъюнкции, конъюнкции и отрицания:

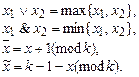
Для k-значных функций, как и в двоичном случае, можно ввести понятия операции, представления функций формулами над заданной системой функций, замыкания, замкнутой и полной системы функций и.т.д. Приведем примеры полных систем k-значных функций.

1. Из представления (4.4) следует, что полной является система функций .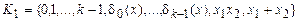

2. Так как в разложении (4.4) операцию сложения можно заменить на дизъюнкцию (выбор максимума), то полной является также система функций .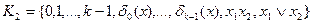

3. Наряду с разложением (4.4) имеет место еще один аналог совершенной дизъюнктивной нормальной формы функции 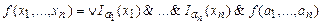, где I_a(x) = 1 как только x = a, и в остальных случаях равна 0. Отсюда следует, что полной является система функций .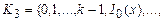

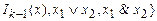4. Система функций 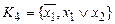является полной системой функций.

Доказательство. С помощью суперпозиции из функции 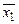легко получить функции 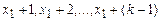. Из них получим константу 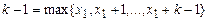, а поэтому все функции константы 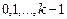. Теперь нетрудно получить функции :

.

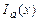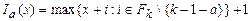Как следует из примера 3, остается построить функцию 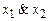, т.е. 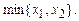Для этого сначала построим функции

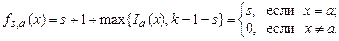
Теперь из них можно получить функции

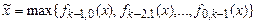
и .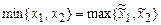

5. Аналогично функции Шеффера в k-значной логике является функция Вебба 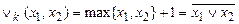, которая одна образует систему, т.е. система 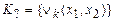является полной.

Доказательство. Используя 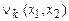, при 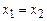имеем 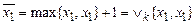. Далее получаем:

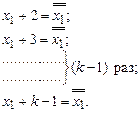
А так как

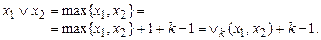
Отсюда имеем, что 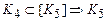— полная система функций.

Утверждение 4.8. Все k-значные функции представляются многочленами над 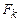в том и только том случае, когда k — простое число, т.е. 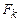поле (без доказательства).

Утверждение 4.9. (Критерий полноты — критерий Слупецкого). Пусть система k-значных функций K содержит все функции одной переменной, причем 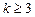. Тогда для полноты системы К необходимо и достаточно, чтобы К содержала функцию, существенно зависящую по меньшей мере от двух переменных и принимающую все 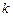значений из .

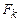Л е к ц и я 5