Решение типовых примеров
Классическая формула вычисления вероятности.
Основные определения и формулы:
Эксперимент, исход которого невозможно предсказать, называют случайным экспериментом (СЭ).
Событие, которое в данном СЭ может произойти, а может и не произойти, называют случайным событием.
Элементарными исходами называют события, удовлетворяющие требованиям:
1. при всякой реализации СЭ происходит один и только один элементарный исход;
2. всякое событие есть некоторая комбинация, некоторый набор элементарных исходов.
Множество всех возможных элементарных исходов полностью описывает СЭ. Такое множество принято называть пространством элементарных исходов (ПЭИ). Выбор ПЭИ для описания данного СЭ неоднозначен и зависит от решаемой задачи.
Если элементарные исходы СЭ обладают свойством равновозможности (в силу определенной “симметрии” условий), то вероятность Р(А) любого события А определяется формулой:
Р(А) = n(A) / n ,
где n – общее число равновозможных исходов,
n(A) – число исходов, составляющих событие А, как говорят еще, благоприятствующих событию А.
Слова “наудачу”, “наугад”, “случайным образом” как раз и гарантируют равновозможность элементарных исходов.
Решение типовых примеров
Пример 1. Из урны, содержащей 5 красных, 3 черных и 2 белых шара, наудачу извлекают 3 шара. Найти вероятности событий:
А – “все извлеченные шары красные”;
В – “ все извлеченные шары – одного цвета”;
С – “среди извлеченных ровно 2 черных”.
Решение :
Элементарным исходом данного СЭ является тройка (неупорядоченная !) шаров. Поэтому, общее число исходов есть число сочетаний: n = 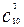 = 120 (10 = 5 + 3 + 2).
= 120 (10 = 5 + 3 + 2).
Событие А состоит только из тех троек, которые извлекались из пяти красных шаров, т.е. n(A)= 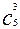 = 10.
= 10.
Событию В кроме 10 красных троек благоприятствуют еще и черные тройки, число которых равно 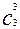 = 1. Поэтому: n(B)=10+1=11.
= 1. Поэтому: n(B)=10+1=11.
Событию С благоприятствуют те тройки шаров, которые содержат 2 черных и один не черный. Каждый способ выбора двух черных шаров может комбинироваться с выбором одного не черного (из семи). Поэтому: n(C) = 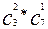 = 3 * 7 = 21.
= 3 * 7 = 21.
Итак: Р(А) = 10/120; Р(В) = 11/120; Р(С) = 21/120.
Пример 2. В условиях предыдущей задачи будем считать, что шары каждого цвета имеют свою нумерацию, начиная с 1. Найти вероятности событий:
D – “максимальный извлеченный номер равен 4”;
Е – “ максимальный извлеченный номер равен 3”.
Решение :
Для вычисления n(D) можно считать, что в урне есть один шар с номером 4, один шар с большим номером и 8 шаров (3к+3ч+2б) с меньшими номерами. Событию D благоприятствуют те тройки шаров, которые обязательно содержат шар с номером 4 и 2 шара с меньшими номерами. Поэтому: n(D) = 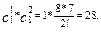
P(D) = 28/120.
Для вычисления n(Е) считаем: в урне два шара с номером 3, два с большими номерами и шесть шаров с меньшими номерами (2к+2ч+2б). Событие Е состоит из троек двух типов:
1. один шар с номером 3 и два с меньшими номерами;
2. два шара с номером 3 и один с меньшим номером.
Поэтому: n(E)= 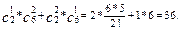
Р(Е) = 36/120.
Пример 3. Каждая из М различных частиц бросается наудачу в одну из N ячеек. Найти вероятности событий:
А – все частицы попали во вторую ячейку;
В – все частицы попали в одну ячейку;
С – каждая ячейка содержит не более одной частицы (M £ N);
D – все ячейки заняты (M=N+1);
Е – вторая ячейка содержит ровно к частиц.
Решение :
Для каждой частицы имеется N способов попасть в ту или иную ячейку. По основному принципу комбинаторики для М частиц имеем N*N*N*…*N (М-раз). Итак, общее число исходов в данном СЭ n = NM.
Для каждой частицы имеем одну возможность попасть во вторую ячейку, поэтому n(A) = 1*1*…*1= 1М = 1, и Р(А) = 1/ NM.
Попасть в одну ячейку (всем частицам) означает попасть всем в первую, или всем во вторую, или и т.д. всем в N-ю. Но каждый из этих N вариантов может осуществиться одним способом. Поэтому n(B)=1+1+…+1(N-раз)=N и Р(В)=N/NM.
Событие С означает, что у каждой частицы число способов размещения на единицу меньше, чем у предыдущей частицы, а первая может попасть в любую из N ячеек. Поэтому:
n (C) = N*(N-1)*…*(N+M-1) и Р(С) = 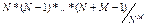
В частном случае при M=N : Р(С)= 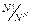
Событие D означает, что одна из ячеек содержит две частицы, а каждая из (N-1) оставшихся ячеек содержит по одной частице. Чтобы найти n(D) рассуждаем так: выберем ячейку в которой будет две частицы, это можно сделать 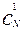 =N способами; затем выберем две частицы для этой ячейки, для этого существует
=N способами; затем выберем две частицы для этой ячейки, для этого существует 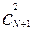 способов. После этого оставшиеся (N-1) частиц распределим по одной в оставшиеся (N-1) ячеек, для этого имеется (N-1)! способов.
способов. После этого оставшиеся (N-1) частиц распределим по одной в оставшиеся (N-1) ячеек, для этого имеется (N-1)! способов.
Итак, n(D) = 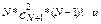
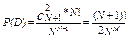 .
.
Число n(E) можно подсчитать так: к частиц для второй ячейки можно 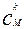 способами, оставшиеся (М – К) частиц распределяются произвольным образом по (N-1) ячейке (N-1)М-К способами. Поэтому :
способами, оставшиеся (М – К) частиц распределяются произвольным образом по (N-1) ячейке (N-1)М-К способами. Поэтому :
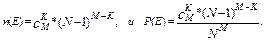
ТЕМА 2. Геометрическая вероятность.
Основные определения и формулы:
Пусть СЭ можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, ПЭИ = G. Если СЭ обладает симметрией возможных исходов, то все точки G “равноправны” и естественно считать, что вероятность попадания точки в некоторое подмножество пропорционально его мере и не зависит от его расположения и формы. Для такого СЭ геометрическая вероятность события А определяется отношением:
Р(А) = m(A) / m(G),
Где m(G), m(A) – геометрические меры (длины, площади или объемы) всего ПЭИ и события А.
Решение типовых примеров:
Пример 1: на плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r (r + d <D). Найти вероятность того, что круг пересечет некоторую полосу.
Решение :
В качестве элементарного исхода этого СЭ будем считать расстояние x от центра круга до осевой линии ближайшей к кругу полосы. Тогда все ПЭИ – это отрезок G = {x: 0£x£D}. Пересечение круга с полосой произойдет в том случае, если его центр попадет в полосу, т.е. 0£x£d, или будет находится от края полосы на расстоянии меньшем чем радиус, т.е. d£x£d+r.
Для искомой вероятности получаем:
Р(А) = (d + r) / D.
Пример 2. По радиоканалу в течение промежутка времени (0;Т) передаются два сигнала длительностью Т1<Т/2; каждый из них с одинаковой возможностью начинается в любой момент интервала (0;Т-Т1). Если сигналы перекроют друг друга хотя бы частично, оба они искажаются. Найти вероятность принятия сигналов без искажений.
Решение :
Обозначим через х момент начала первого сигнала, у – второго. Все ПЭИ можно представить в виде квадрата:
G = {(x,y): 0<x<T-T1, 0<x<T-T1}.
Сигналы не п0ерекроются, если длительность Т1 меньше, чем время между началами сигналов, т.е. интересующее нас событие:
А = “сигналы не искажены”= {(x,y): |x – y|>T1}.
Это множество состоит из двух одинаковых равнобедренных треугольников в углах квадрата G, катеты которых равны Т – 2Т1. Поэтому вероятность равна:
Р(А) = (Т – 2Т1)2 / (Т – Т1)2
ТЕМА 3. Теоремы сложения и умножения.
Основные определения и формулы:
Сумма событий А и В есть событие А+В, состоящее в наступлении хотя бы одного из событий А или В.
Произведение событий А и В есть событие А*В, состоящее в совместном наступлении обоих событий А и В.
События называются несовместными, если их совместное наступление невозможно.

 Противоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.
Противоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.
Некоторые свойства:
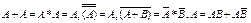
Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью Р(А/В).
События А и В называются независимыми, если Р(А/В) = Р(А) (или Р(В/А) = Р(В)).
Теорема умножения 1.(ТУ1): Р(АВ) = Р(А)*Р(В/А) = Р(В)*Р(А/В).
ТУ 2.: вероятность совместного наступления независимых событий равна произведению их вероятностей.
Теорема сложения 1.(ТС1): вероятность суммы попарно несовместных событий равна сумме их вероятностей.
 |
ТС 2.: Р(А) = 1 – Р(А).
ТС 3.: Р(А+В) = Р(А) + Р(В) – Р(АВ).
Решение типовых примеров :
Пример 1. Из урны, содержащей 5 красных и 7 белых шаров, наудачу извлекают по одному два шара. Найти вероятности событий :
В – извлеченные шары – белые;
С – только первый извлеченный шар – белый;
D – только один извлеченный шар – белый.
Рассмотреть два случая: а) извлечения без возвращения; б) извлечения с возвращением.
Решение :
Обозначим : Ак – к-й извлеченный шар – белый, к = 1 .. 2. Тогда
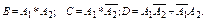
а) если 1й шар не возвращают в урну, то вероятности событий, связанных со вторым извлечением зависят от исхода первого, т.е. А1 и А2 – зависимые события и поэтому:
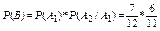 .
.
Условную вероятность нашли, рассуждая так: после того, как событие А1 произошло, т.е. первый извлеченный шар был белый, второе извлечение осуществляется из урны, содержащей 5 красных и 6 белых (7 – 1 = 6) шаров. Поэтому Р(А2 /А1) = 6 /11.
Аналогично 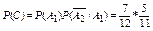 .
.
Слагаемые в записи события D являются несовместными, поэтому:
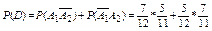 .
.
б) в случае возвращения извлеченного шара извлечения становятся независимыми испытаниями, а значит и события, связанные с ними – независимые, причем Р(А1) = Р(А2) = 7/12. Поэтому:
Р(В) = (7 / 12)2; Р(С) = 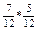 ; Р(D) =
; Р(D) = 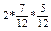 .
.
Пример 2. Из колоды карт (36 карт, 4 масти) извлекают наудачу сразу 3 карты. Найти вероятности событий :
А – среди извлеченных карт есть 2 бубны или 2 туза;
В – извлечена хотя бы одна дома.
Решение :
Событие А – это сумма событий : А1 – среди извлеченных карт есть 2 бубны, А2 – среди извлеченных карт есть 2 туза. Эти события – совместные и их произведение А1*А2 – среди извлеченных карт есть 2 бубны и 2 туза – может осуществиться только так : среди извлеченных карт есть туз бубновый, еще один туз из трех “не бубновых” и еще одна бубна из восьми “нетузов”. Поэтому n(A1A2) = 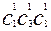 .
.
Применяя ТС3 и классическую формулу вычисления вероятности, находим :
Р(А) = Р(А1) + Р(А2) – Р(А1А2) = 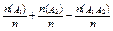 =
=
= 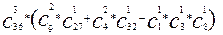 .
.
Чтобы найти Р(В), перейдем к противоположному событию : 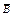 – среди извлеченных нет дам, т.е. все “не дамы” :
– среди извлеченных нет дам, т.е. все “не дамы” :
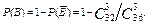
Пример 3. Вероятность попадания в цель в каждом из n независимых выстрелов равна р. выразить через n и р вероятность Р хотя бы одного попадания в n выстрелах.
a) Найти Р для n = 3, р = 0,7 ;
b) Пусть р = 0,6. Сколько выстрелов нужно сделать, чтобы с вероятностью не меньшей 0,97 попасть хотя бы один раз?
c) Пусть n = 5. Какова должна быть вероятность попадания р в каждом выстреле, что бы с вероятностью не меньшей 0,95 попасть хотя бы один раз?
Решение :
Обозначим через Ак – “попадание” и 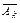 – “промах” при к-ом выстреле. Тогда для события В – хотя бы одно попадание в n выстрелах, можно записать:
– “промах” при к-ом выстреле. Тогда для события В – хотя бы одно попадание в n выстрелах, можно записать:
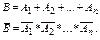
Применяя ТС1 и ТУ2, получим:
Р(В) = 1 – Р(В) = 1 – Р(А1)* Р(А2)* … * Р(Аn) = 1 – (1 – Р(А1))n
Итак, Р = 1 – (1 – р)n.
a) вероятность хотя бы одного попадания в 3х выстрелах (при условии, что при каждом выстреле вероятность попадания равна 0,7):
Р = 1 – (1 – 0,7)3 = 0,973
b) нахождение требуемого числа выстрелов n сводится к решению неравенства :
0,97 £ 1 – (1 – 0,6)n или 0,4n £ 0,03.
Отсюда получаем для n :
n ³ lg 0,03 / lg 0,4 = 3,83
Итак, необходимо сделать не менее 4х выстрелов.
c) искомая вероятность р удовлетворяет неравенству:
1 – (1 – р)5 ³ 0,95 или (1 – р) £ 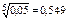
Отсюда получаем: р ³ 0,451.
Пример 4. Первый стрелок попадает в цель с вероятностью р1, а второй – р2. Найти вероятности событий :
В – попал только первый стрелок;
С – попал только один стрелок;
D – попал хотя бы один стрелок.
если каждый сделал по одному выстрелу.
Решение :
Обозначим через Ai – попадание, 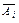 – промах i-го стрелка, i = 1 .. 2. “Попал только первый” подразумевает, что второй промахнулся, т.е.
– промах i-го стрелка, i = 1 .. 2. “Попал только первый” подразумевает, что второй промахнулся, т.е. 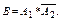 “Попадание только одного” есть сумма двух слагаемых : “попал только первый” и “попал только второй”, т.е.
“Попадание только одного” есть сумма двух слагаемых : “попал только первый” и “попал только второй”, т.е. 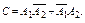 Для события D можно написать различные представления:
Для события D можно написать различные представления:
D = A1 + A2 (слагаемые совместные);
D = C + A1A2 (слагаемые несовместные);
D = “не попал ни один” = 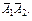
Теоремы сложения и умножения позволяют найти требуемые вероятности :
Р(В) = р1*(1 – р2);
Р(С) = р1*(1 – р2) + р2*(1 – р1);
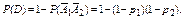
Пример 5. Независимые события производятся до тех пор, пока не произойдет событие А, причем: вероятность появления А в каждом испытании одна и та же и равна р. найти вероятности событий :
В – опыт закончится на третьем испытании;
С – потребуется нечетное число испытаний;
D – потребуется не менее трех испытаний.
Решение :
Обозначим через Ак – появление и 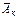 – непоявление события А в к-ом испытании, к = 1, 2, … . По условию Р(Ак) = р,
– непоявление события А в к-ом испытании, к = 1, 2, … . По условию Р(Ак) = р, 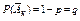 . Окончание опыта на третьем испытании означает, что в первых двух испытаниях событие А не происходило, а в третьем – произошло, т.е. В = А1*А2*А3.
. Окончание опыта на третьем испытании означает, что в первых двух испытаниях событие А не происходило, а в третьем – произошло, т.е. В = А1*А2*А3.
В общем случае, если Bn – опыт закончится на п-ом испытании, - то можно записать:
В = А1*А2* … *Аn – 1*An и C = 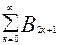 .
.
Для события D можно записать аналогичное равенство:
D = 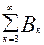 .
.
Можно также рассмотреть 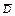 – менее трех испытаний, т.е. “два испытания или одно”: D =
– менее трех испытаний, т.е. “два испытания или одно”: D = 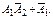 Но лучше рассуждать так: потребуется три и более испытаний только тогда, когда в первых двух событие А не произошло, т.е. D =
Но лучше рассуждать так: потребуется три и более испытаний только тогда, когда в первых двух событие А не произошло, т.е. D = 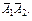
Используя теоремы сложения и умножения, получаем:
Р(В) = q2*p ; P(D) = q2 ;
P(C) = 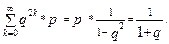
ТЕМА 4. Формулы полной вероятности и Байеса.
Основные определения и формулы :
Пусть событие А может произойти только совместно с одним из попарно несовместных событий Н1, Н2, … , Нn (это имеет место, например, для полной группы событий Нк, к = 1.. n). Тогда:
Р(А) = 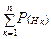 Р(А/Нк). (формула полной вероятности).
Р(А/Нк). (формула полной вероятности).
Если при этом Р(А) ¹ 0, то
Р(Нm/А) = 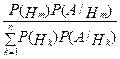 , m = 1 .. n . (формула Байеса).
, m = 1 .. n . (формула Байеса).
Выбор подходящих гипотез Н1, Н2, … , Нn зависит от того, можем ли мы достаточно просто вычислить условные вероятности Р(А/Нк).
Решение типовых примеров:
Пример 1. Из урны, содержащей 10 черных и 5 белых шаров, извлекают один и, выяснив его цвет, добавляют в урну к шаров противоположного цвета. Чему равно к, если вероятность извлечь после этого белый шар равна 0,5?
Решение :
Обозначим через А событие, состоящее в том, что шар, извлеченный из урны после изменения её состава, имеет белый цвет. Это событие тесно связано с двумя гипотезами относительно цвета первого извлеченного шара:
Н1 – шар, первоначально извлеченный из урны – черный;
Н2 – шар, первоначально извлеченный из урны – белый;
Вероятности этих гипотез: Р(Н1) = 10/15 ; Р(Н2) = 5/15.
Осуществление гипотезы Н1, означает, что второй шар извлекают из урны, содержащей 9 (=10–1) черных и 5+к белых шаров, а появление события Н2 приведет к такому составу: 4 (=5–1) белых шара и 10+к черных. Поэтому, условные вероятности:
Р(А/Н1) = (5+к) / (14+к) ; Р(А/Н2) = 5 / (14+к).
Формула полной вероятности:
Р(А) = 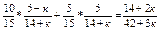 .
.
По условию эта вероятность равна 0,5.
Отсюда находим к:
к = 14.
Пример 2. Вероятность попадания в цель при каждом выстреле равна 0,8. Вероятность поражения цели при к попаданиях равна 1 – 0,3к. Найти вероятность поражения цели, если сделано 2 выстрела.
Решение :
Интересующее нас событие А – цель поражена – может произойти только совместно с одним из событий:
Н1 – одно попадание в 2х выстрелах;
Н2 – два попадания.
Если Вк – попадание в к-ом выстреле, то
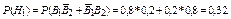
Р(Н2) = Р(В1В2) = 0,8*0,8 = 0,64.
Найдем условные вероятности:
Р(А/Н1) = 1 – 0,31 = 0,7 ; Р(А/Н2) = 1 – 0,32 = 0,91.
Полная вероятность события равна:
Р(А) = 0,32*0,7 + 0,64*0,91 = 0,8064.
Пример 3. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение :
Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: Нк – взятая наудачу деталь обработана на к-ом станке, к = 1..3.
Условные вероятности (в условии задачи они даны в форме процентов):
Р(А/Н1) = 0,02 ; Р(А/Н2) = 0,07 ; Р(А/Н3) = 0,1.
Зависимости между производительностями станков означают следующее: Р(Н1) = 3Р(Н2), Р(Н3) = 0,5Р(Н2). А т.к. гипотезы образуют полную группу, то Р(Н1) + Р(Н2) + Р(Н3) = 1.
Решив полученную систему уравнений, найдем:
Р(Н1) = 6/9 ; Р(Н2) = 2/9 ; Р(Н3) = 1/9.
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
Р(А) = 6/9 * 0,02 + 2/9 * 0,07 + 1/9 * 0,1 = 0,04.
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
Р(Н1/А) = [6/9 * 0,02] / 0,04 = 0,33 ;
Р(Н2/А) = [2/9 * 0,07] / 0,04 = 0,39;
Р(Н3/А) = 1 – Р(Н1/А) – Р(Н2/А) = 0,28.
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
ТЕМА 5. Повторение опытов.
Основные определения и формулы :
Пусть осуществляется n независимых повторений некоторого эксперимента (или n независимых экспериментов), в каждом из которых может произойти событие А.
Если вероятность этого события в каждом испытании равна р, то вероятность Р(n;k) того, что в n испытаниях событие А наступит ровно к раз определяется формулой Бернулли :
Р(n;k) = 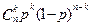 .
.
В случае когда вероятность события А в m-ом испытании равна pm , m = 1.. n, вероятность Р(n;k) равна коэффициенту при zk в разложении производящей функции :
G(z) = 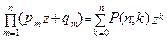 ,
,
где qm = 1 – рm.
Другое обобщение формулы Бернулли состоит в следующем. Пусть в каждом из независимых испытаний может появиться одно из m несовместных событий Ai и P(Ai) = pi во всех испытаниях, 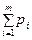 =1. Тогда вероятность Р(n;k1;k2;…;km) того, что в n испытаниях событие Ai произойдет ki раз, i = 1..m,
=1. Тогда вероятность Р(n;k1;k2;…;km) того, что в n испытаниях событие Ai произойдет ki раз, i = 1..m, 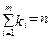 , определяется полиномиальной формулой:
, определяется полиномиальной формулой:
P(n;k1;k2;…;km) = 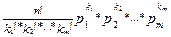 .
.
Наиболее вероятное число m0 появлений события А в n испытаниях (если в каждом испытании Р(А) = р) равно целой части числа р(n+1). Если р(n+1) – целое, то наибольшее значение вероятности Р(n;k) достигается при двух числах: m0 = р(n+1) и m0 = 1.
Замечание. Некоторые задачи, связанные с повторением испытаний, не требуют для своего решения использования специальных формул, а решаются на основании теорем сложения и умножения.
Решение типовых примеров:
Пример 1. В продукции некоторого производства брак составляет 10%. Наудачу отбираются семь изделий. Найти вероятности событий :
В – среди отобранных – 2 бракованных;
С – не более двух бракованных;
D – хотя бы одно бракованное.
Решение :
Отбор одного изделия – это испытание, в котором может появиться событие А – изделие является бракованным, причем р=Р(А)=0,1. По условию задачи проведено семь таких испытаний. Вероятность события В сразу находим по формуле Бернулли:
Р(В) = Р(7;2) = 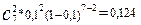 .
.
Для события С можно написать: С = С0 + С1 + С2, где Ск – среди отобранных ровно к бракованных. Используя теорему сложения, получим:
Р(С) = Р(7;0) + Р(7;1) + Р(7;2) = 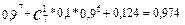
Как интерпретировать полученный результат? Будем считать, что изделия укладываются в коробки по 7 штук, причем, если в коробке оказалось не более двух бракованных, то её назовем “хорошей”. Полученный результат для Р(С) означает, что 97,4% всех коробок являются “хорошими”.
Для вычисления P(D) нет необходимости применять формулу Бернулли, а достаточно перейти к 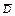 – все изделия стандартные и применить одну из теорем сложения:
– все изделия стандартные и применить одну из теорем сложения:
P(D) = 1 – 0,97 = 0,522.
Пример 2. Имеется n перенумерованных урн, в каждой из которых n шаров, причем в к-ой урне ровно к черных и n-k белых, к = 1..n. Из каждой урны наудачу извлекают по одному шару. Найти вероятность P(n;k) того, что среди n извлеченных шаров ровно к черных? Рассмотреть частный случай, когда n = 4, к = 2.
Решение :
Извлечение шара из урны – это испытание, в котором может появиться интересующее нас событие А – шар черный. Однако вероятность события зависит от номера испытания: для к-ой урны Р(А) = рк = к / n, qk = (n – k) / n, k = 1.. n. Составляем производящую функцию:
G(z) = 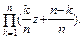
Искомая вероятность P(n;k) есть коэффициент при zk в разложении этой функции:
G(z) = 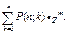
Коэффициенты такой функции можно найти дифференцированием:
P(n;k) = 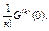
В частном случае имеем:
G(z) = 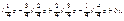
Коэффициент при z3 – это искомая вероятность:
Р(4;3) = 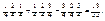
Пример 3. В каждом выстреле стрелок наверняка попадает в мишень, состоящую из четырех перенумерованных частей, причем вероятность попасть в каждую часть пропорциональна ее номеру. Найти вероятность того, что в пяти выстрелах стрелок 1 раз попадет в первую часть и по два раза в третью и четвертую.
Решение :
Каждый выстрел – это испытание, в котором может произойти одно из четырех событий: Ак – стрелок попал в часть мишени с номером к, к = 1..4. По условию Р(Ак) = рк = М*к и 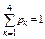 . Для коэффициента пропорциональности М имем:
. Для коэффициента пропорциональности М имем:
М*1 + М*2 + М*3 + М*4 = 1, откуда М = 0,1.
Итак, р1 = 0,1 ; р2 = 0,2 ; р3 = 0,3 ; р4 = 0,4.
Искомая вероятность есть вероятность Р(5; 1, 0, 2, 2) того, что в пяти испытаниях событие А1 произошло 1 раз, А2 – ни разу, А3 и А4 – по 2 раза. Полиномиальная формула дает ответ:
Р(5; 1, 0, 2, 2) = 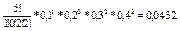
Пример 4. Из урны, содержащей 3 черных и 4 белых шара, извлекают по одному с возвращением несколько шаров: а) Найти наиболее вероятное число появлений черного шара в 10-ти извлечениях; в 20-ти извлечениях. б) Сколько нужно произвести извлечений, чтобы наивероятнейшее число появлений черного шара было равно 7?
Решение :
Обозначим: А – извлечен черный шар. Тогда: р = Р(А) = 3/7.
а) для 10-ти извлечений имеем: (n+1)p = 11*3/7»4,7. Целая часть этого числа m0 = 4. Это и есть наиболее вероятное число появлений черного шара в 10-ти извлечениях.
Для 20-ти извлечений имеем: (n+1)p = 21*3/7»9. Это число целое, поэтому существуют два значения m0 = 9 и m1 = 8, при которых вероятность Р(20;к) того, что в 20-ти извлечениях черный шар появится к раз, достигает наибольшего значения. Найдем это значение:
Р(20;9) = 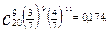
б) исходя из того, что наивероятнейшее число m0 появлений события А является целой частью числа р(n+1), можно написать двойное неравенство:
np – q £ m0 £ np + p, где q = 1 – p.
Отсюда для n можно получить:
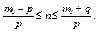
Для наших условий р = 3/7, q = 4/7, m0 = 7:
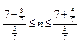 или 15,3 £ n £ 17,6.
или 15,3 £ n £ 17,6.
Таким образом, если число извлечений равно 16 или 17, то наиболее вероятное число появлений черного шара равно 7.
Пример 5. Независимые испытания продолжаются до тех пор, пока событие А не произойдет к раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них Р(А) = р.
Решение :
Событие В – n испытаний до к-го появления события А – есть произведение двух таких событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
Р(В) = Р(С)*Р(D) = P(n–1; k–1)*P(A) = 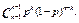
ТЕМА 6. Повторение опытов (при большом N).
Основные определения и формулы:
Пусть в каждом из независимых испытаний событие А может произойти с вероятностью q, q = 1 – p. Обозначим как и раньше, через P(n;k) вероятность ровно к появлений события А в n испытаниях. кроме того, пусть P(n; k1, k2) – вероятность того, что число появлений события А находится между к1и к2.
Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то
P(n;k) 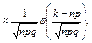
где 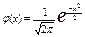 - функция Гаусса.
- функция Гаусса.
Интегральная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то
P(n; k1, k2) 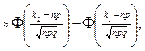
где 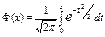 - функция Лапласа.
- функция Лапласа.
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций: а) j(-х) = j(х), F(-х) = -F(х); б) при больших х j(х) » 0, F(х) » 0,5.
Теоремы Лапласа дают удовлетворительное приближение при npq ³ 9.
Теорема Пуассона. Если n – велико, а р – мало, то
P(n;k) 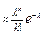 , где l = n*p.
, где l = n*p.
Эта формула дает удовлетворительное приближение для р £ 0,1и np £ 10. При больших np рекомендуется применять формулы Лапласа.
Решение типовых примеров :
Пример 1. Пусть т – число появлений события А в n независимых испытаниях. Чему равна вероятность того, что частота т/п события А отклонится от его вероятности р не более чем на e?
Решение :
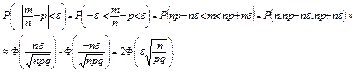
Итак, искомая вероятность приближенно равна 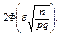
Пример 2. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий:
В – наудачу взятая коробка содержит 13 бракованных изделий;
С – число бракованных изделий в коробке не превосходит 20
Решение :
Изготовление детали – это испытание, в котором может появиться событие А – изделие бракованное – с вероятностью р = 0,15. Находим пр = 15, npq = 12,75. Можно применять формулы Лапласа:
Р(В) = Р(100;13) 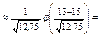 0,28j(-0,56) = 0,28*0,341 = 0,095.
0,28j(-0,56) = 0,28*0,341 = 0,095.
Р(С) = Р(100; 0, 20) 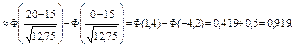
Значения функций Гаусса и Лапласа нашли по таблицам с учетом их свойств. Как интерпретировать результат? Приблизительно 9,5% всех коробок содержат 13 бракованных изделий и в 92% коробок число бракованных не превосходит 20.
Пример 3. Известно, что только 80% семян некоторой культуры дают полноценные растения. Сколько семян нужно посадить, чтобы с вероятностью не меньшей 0,95 получить, по крайней мере, 100 растений?
Решение :
Поведение семян в почве – это испытание, событие А – семя дало полноценное растение, р = 0,8. Неизвестное число испытаний п должно удовлетворять неравенству:
Р(п; 100, п) ³ 0,95, причем п > 100.
Используем формулу Лапласа:
Р(n; 100, n) 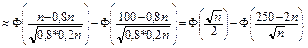
Учитывая свойства функции Лапласа, получим:
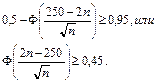
Из таблицы значений функции Лапласа находим: 0,45 = F(1,645). Учитывая еще и возрастание F(х) получаем неравенство для определения п:
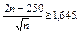
Решая его, получаем: 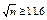 , т.е. п ³135.
, т.е. п ³135.
Итак, посеяв 135 (или более) семян можно с вероятностью 0,95 гарантировать получение, по крайней мере, 100 полноценных растений.
Пример 4, имеется АТС, которая обслуживает 1000 абонентов. Для каждого их них вероятность воспользоваться услугами АТС в течении одной минуты равна 0,003. Для выбранной наудачу минуты найти вероятности событий: В – ровно 5 вызовов на АТС, С – не более двух вызовов, D – хотя бы один вызов.
Решение :
Поведение абонента в течении одной минуты – это испытание, событие А – абонент воспользовался услугами АТС, р = 0,003, nр = 3. Используем формулу Пуассона, причем l = 3:
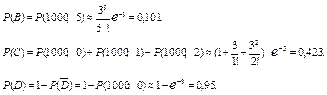
ТЕМА 7. Дискретная случайная величина.
Основные определения и формулы :
Случайной величиной (СВ) называется величина, которая в результате СЭ может принять то или иное значение, заранее неизвестное и зависящее от случайных причин.
Если множество возможных значений СВ представляет собой последовательность чисел (конечную или бесконечную), то такая СВ называется дискретной (ДСВ).
Случайная величина полностью описывается (с вероятностной точки зрения) заданием своего закона распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями СВ и вероятностями принять эти значения.
Для ДСВ закон распределения можно задавать в различных формах: табличной, графической, аналитической.
Рядом распределения ДСВ называется таблица вида:
| Х | х1 | х2 | … | хк | … |
| Р | р1 | р2 | … | рк | … |
где хк – все возможные значения ДСВ Х,
рк – соответствующие вероятности, т.е. рк = Р(Х=хк), к = 1,2,…, причем S рк = 1.
Многоугольником распределения ДСВ Х называется ломаная линия, звенья которой последовательно соединяют точки (хк, рк), нанесенные на координатную плоскость хОр.
Функцией распределения произвольной СВ Х называется функция F(x) действительного переменного х, определяемая равенством:
F(x) = P(X < x).
Для ДСВ функция распределения всегда есть разрывная ступенчатая функция, скачки которой расположены в точках, соответствующих возможным значениям СВ, и равны вероятностям этих значений. Формально:
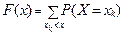
К числовым характеристикам ДСВ Х относятся: математическое ожидание М(Х), дисперсия D(Х), среднее квадратичное отклонение s (Х), коэффициент вариации V(Х), асимметрия А(Х), эксцесс Е(Х), мода М (формулу для вычисления см. в примере 1).
Решение типовых примеров :
Дата добавления: 2022-05-27; просмотров: 261;
<== предыдущая лекция
|
следующая лекция ==>
ВИДЫ ЭКОНОМИЧЕСКОГО АНАЛИЗА | СОСТАВЛЕНИЕ ТЕХНИЧЕСКОГО ПАСПОРТА










