Числа, отличные от натуральных

В предыдущих параграфах мы рассма­тривали действия над натуральными числа­ми и отметили тот замечательный факт, что машина Тьюринга может оперировать с на­туральными числами произвольной величи­ны, несмотря на то, что каждая машина имеет фиксированное и конечное число вну­тренних состояний. Однако часто возникает необходимость в операциях с более сложны­ми числами, такими как отрицательные чи­сла, обыкновенные дроби и бесконечные де­сятичные дроби. Первые две категории (т. е. числа вида —597/26) легко поддаются обра­ботке машинами Тьюринга, причем и чи­слители, и знаменатели могут быть сколь угодно большими. Все, что для этого нуж­но — какой-нибудь подходящий код для знаков «—» и «/», который можно легко выбрать при использовании расширенной двоичной записи (например, «3» = 1110для знака «-», а «4» = 11110— для зна­ка «/»). Таким образом, отрицательные чи­сла и обыкновенные дроби рассматривают­ся как конечные наборы натуральных чисел, и с точки зрения общих вопросов вычисли­мости ничего нового не дают.

То же можно сказать и о конечных деся­тичных выражениях с произвольным числом знаков после запятой, поскольку они пред­ставляют собой лишь частный случай обык­новенных дробей. Так, например, конечная десятичная аппроксимация иррационально­го числа w, заданная числом 3,14159265, есть просто дробь 314 159265/100000000. Одна­ко бесконечные десятичные выражения, та­кие как полная запись числа пи

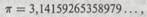
представляют определенные трудности. На самом деле, ни входные, ни выходные данные машины Тьюринга не могут быть беско­нечными десятичными выражениями. Мож­но было бы думать, что нашлась бы ма­шина Тьюринга, способная выдавать одну за другой все последовательные цифры - 3, 1, 4, 1, 5, 9, ... в десятичной записи чи­сла пии переносить их на выходную ленту, а мы просто позволим этой машине работать бесконечно долго. Но это запрещено для ма­шин Тьюринга. Мы должны дождаться оста­новки машины (сопровождаемой звонком колокольчика!), прежде чем сможем озна­комиться с результатом. До того момента, пока машина не выполнит команды STOP, выходные данные могут изменяться и по­этому не являются достоверными. С другой стороны, после полной остановки машины результат должен быть с необходимостью конечным.

Существует, однако, «законная» про­цедура для того, чтобы заставить машину Тьюринга последовательно воспроизводить цифры примерно так, как это предлагалось выше. Если мы хотим получить бесконеч­ную десятичную запись, скажем, числа ж, мы могли бы заставить машину Тьюрин­га сначала рассчитать его целую часть, 3, используя на входе 0, затем — первую ци­фру дробной части, 1, используя на вхо­де 1, затем — вторую цифру дробной ча­сти, 4, используя на входе 2, потом — третью цифру, 1, используя 3 и т. д. Во­обще говоря, машина Тьюринга для по­лучения всех цифр десятичной записи чи­сла тг в этом смысле действительно суще­ствует, хотя реализовать ее в явном виде было бы затруднительно. Подобное же заме­чание относится и ко многим другим ирра­циональным числам, таким, например, как 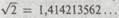. Однако оказывает­ся—и мы увидим это в следующей главе, — что некоторые иррациональные числа прин­ципиально не могут быть получены с по­мощью машины Тьюринга. Числа, которые можно получить таким образом, называют­ся вычислимыми (Тьюринг [1937]), а осталь­ные (в действительности абсолютное боль­шинство!) — невычислимыми. Я еще вернусь к этой теме и затрону ряд смежных вопросов в последующих главах. К нам это имеет от­ношение в связи с вопросом о том, может ли реальный физический объект (например, человеческий мозг) быть адекватно опи­сан в терминах вычислимых математических структур в соответствии с нашими физиче­скими теориями.

Проблема вычислимости важна для ма­тематики в целом. Не следует думать, что она относится только к числам как таковым. Ведь машины Тьюринга могут непосредственно оперировать математическими формулами, например, алгебраическими или тригономе­трическими выражениями, или выполнять формальные действия математического ана­лиза. Все, что для этого нужно, это некий способ точного кодирования всех использу­емых математических символов в виде по­следовательностей нулей и единиц, которые позволят применить соответствующую ма­шину Тьюринга. Именно это Тьюринг имел в виду, когда он взялся за проблему алгорит­мической разрешимости, в которой требует­ся найти алгоритмическую процедуру для ответа на самые общие математические во­просы. Очень скоро мы вновь обратимся к этой теме.