Примеры определения перемещений при изгибе графоаналитическим методом и по универсальным уравнениям
Пример. 2. Определить прогиб свободного конца консольной балки с сосредоточенной нагрузкой на конце (рис. VII.7, а).
Р е ш е н и е. Помещаем начало координат в заделке, тогда u0 = 0 и J0 = 0. Строим эпюру изгибающих моментов. Центр тяжести эпюры на расстоянии 2l/3 от правого конца. По формуле (VII.13) определяем EIJв как площадь эпюры М между началом координат и сечением В:
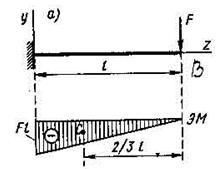 рис. 7.7.
рис. 7.7.
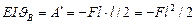
Знак минус берем потому, что эпюра М отрицательна, откуда 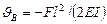 , (по часовой стрелке).
, (по часовой стрелке).
По формуле (VII.16) прогиб определяем как статический момент всей площади эпюры относительно сечения В:
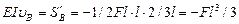
откуда 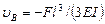 (в направлении отрицательной оси у, т.е. вниз). Знак минус при вычислении S'в взят потому, что эпюра М отрицательна.
(в направлении отрицательной оси у, т.е. вниз). Знак минус при вычислении S'в взят потому, что эпюра М отрицательна.
Пример VII.3. Определить прогиб свободного конца консольной балки, показанной на рис. VII.7, б.
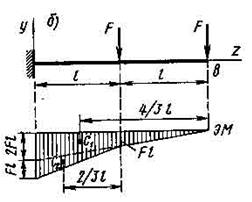 Р е ш е н и е. Помещаем начало координат в заделке, тогда u0 = 0 и J0 = 0.
Р е ш е н и е. Помещаем начало координат в заделке, тогда u0 = 0 и J0 = 0.
Эпюру изгибающих моментов «расслаиваем», т. е. представляем ее как сумму эпюр от действия каждой силы (два треугольника).
По формуле (VII.13) определим угол поворота:
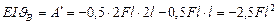 (по часовой стрелке).
(по часовой стрелке).
По формуле (VII. 16) определим прогиб:
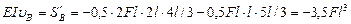 (вниз).
(вниз).
Площадь и статический момент эпюры моментов взяты со знаком минус, так как эпюра М отрицательна.
Пример V11.4. Определить прогиб под нагрузкой для балки, показанной на рис. VII.8.
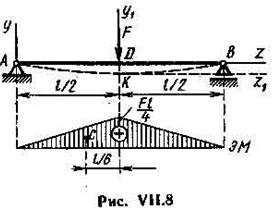 Р е ш е н и е. Помещаем начало координат на левом конце, тогда u0 = 0.
Р е ш е н и е. Помещаем начало координат на левом конце, тогда u0 = 0.
Строим эпюру М.
Для определения J0 используем условие 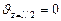 (ввиду симметрии изогнутой оси балки). По формуле (VII.13) имеем
(ввиду симметрии изогнутой оси балки). По формуле (VII.13) имеем
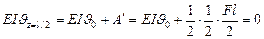 ,
,
откуда 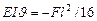 (по часовой стрелке).
(по часовой стрелке).
Площадь А' взята со знаком плюc, потому что эпюра М положительна.
По формуле (VII.16) найдем
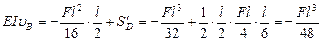 (вниз) (VII.23)
(вниз) (VII.23)
Знак плюс при вычислении S'D взят потому, что эпюра М положительна. Этот пример можно решить проще, если поместить начало координат в точке K. Тогда u0 = 0 и J0 = 0. Перемещение точки В относительно точки K найдем по формуле (VII.16):
 (вверх)
(вверх)
Следовательно, 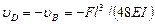 (вниз)
(вниз)
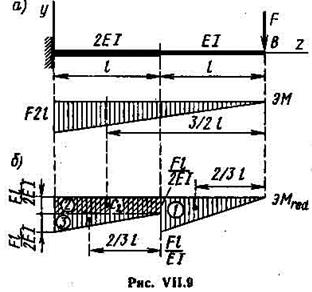 Пример VI1.5. Определить прогиб свободного конца балки, показанной на рис. VII.9, а.
Пример VI1.5. Определить прогиб свободного конца балки, показанной на рис. VII.9, а.
Р е ш е н и е. Помещаем начало координат в заделке, тогда u0 = 0 и J0 = 0. Строим эпюру М и приведенную эпюру Мred, в которой ординаты М поделены на жесткость балки (рис. VII.9, б).
По формуле (VII. 17) имеем
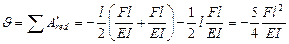 (по часовой стрелке)
(по часовой стрелке)
Разбивая эпюру на три простейших фигуры 1, 2, 3 получим по формуле (VII. 18)
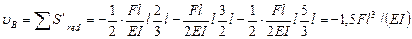 (вниз)
(вниз)
Пример VII.6. Определить прогиб среднего сечения балки, показанной на рис. VII. 10, а.
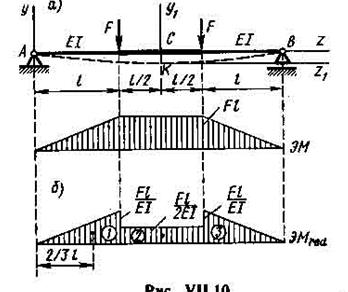 Решение. Помещаем начало координат на левом конце балки, тогда u0 = 0 Строим эпюру М и приведенную эпюру Мred, которой ординаты М поделены на жесткость балки (рис. VII. 10, б).
Решение. Помещаем начало координат на левом конце балки, тогда u0 = 0 Строим эпюру М и приведенную эпюру Мred, которой ординаты М поделены на жесткость балки (рис. VII. 10, б).
Для определения J0 используем условие uz=1,5l = 0 (ввиду симметрии).
По формуле (VII.17) имеем uc = J0 +Ared или
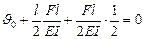
Откуда 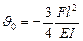 (по часовой стрелке). Определяем прогиб при z = 1,5 l по формуле (VII.18)
(по часовой стрелке). Определяем прогиб при z = 1,5 l по формуле (VII.18)
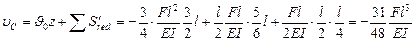 (вниз)
(вниз)
Этот пример можно решить проще, если, используя симметрию, поместить начало координат в точке К. Тогда перемещение точки В относительно точки К по формуле (VII. 18) будет равно (при u0 = J0 = 0)
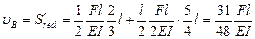 (вверх)
(вверх)
Следовательно, 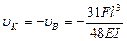 (вниз)
(вниз)
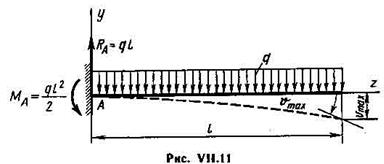
Пример VII.7. Определить по универсальным уравнениям максимальные прогиб и угол поворота для консоли при действии равномерно распределенной нагрузки (рис. VII.11).
 Решение. Начало координат выгоднее поместить на левом конце балки, так как при этом u0 = 0 и J0 = 0
Решение. Начало координат выгоднее поместить на левом конце балки, так как при этом u0 = 0 и J0 = 0
Следовательно, по универсаль- ным уравнениям (VII.21) и (VII.22) сразу можно вычислить umax и Jmax, которые, как видно из чертежа, будут иметь место в сечении, где z = l.
Чтобы пользоваться универсальными уравнениями, необходимо, как уже было сказано, брать силы и моменты, находящиеся между данным сечением и началом координат. Для этого предварительно определим реактивный момент и реактивную силу в заделке.
Реактивная сила RA =ql и направлена вверх. В универсальные уравнения она войдет со знаком плюс. Реактивный момент MA = ql2 /2 направлен против часовой стрелки. Его следует учитывать со знаком минус.
Расстояние от начала координат до момента, опорной реакции и до начала равномерно распределенной нагрузки равны нулю (рис.)
Определяем u при z = l, т.е. umax :
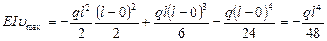 .
.
Следовательно, 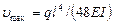 (вниз)
(вниз)
Из универсального уравнения для углов поворота получим
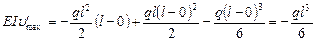
Следовательно, 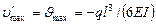 (по часовой стрелке)
(по часовой стрелке)
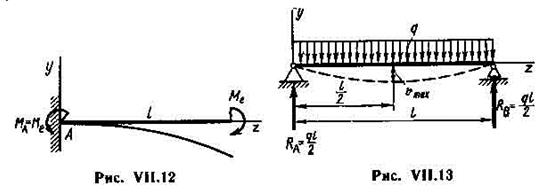
Пример VП.8. Определить umax и u¢max для консольной балки при действии пары Ме на свободном конце (рис. VII.12).
Р е ш е н и е. Начало координат помещаем на левом конце балки. Тогда u0 = 0 и J0 = 0. Опорные реакции равны RA = 0, а МA = М и направлен против часовой стрелки.
Значения umax и u¢max будут на правом конце балки при z = l. Применяя универсальные уравнения, получим:
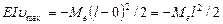 ,
, 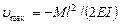 (вниз) (VII.26)
(вниз) (VII.26)
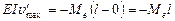 ,
, 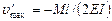 (VII.27)
(VII.27)
Пример V11.9. Определить umax и Jmax для балки, показанной на рис. VII. 13.
Р е ш е н и е. В силу симметрии реакции равны RA = RB = ql/2
Помещаем начало координат на левой опоре. Тогда u0 = 0.
Для определения J0 используем условие, что при z = l u = 0. Получим
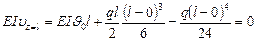 ,
,
Откуда 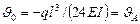 . Очевидно, JA = - JB.
. Очевидно, JA = - JB.
Заметим, что наибольшие углы поворота имеют опорные сечения. Максимальный прогиб находится посередине пролета балки:
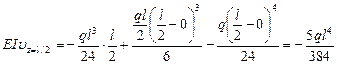
Следовательно, 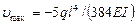 (вниз). (VII.28)
(вниз). (VII.28)
Пример VII.10. Определить максимальный прогиб и угол поворота на опорах для балки, нагруженной посередине пролета сосредоточенной силой (рис. VII. 14).
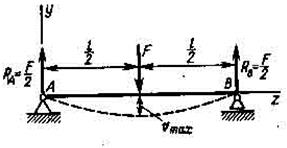
Р е ш е н и е. Реакции равны F/2 каждая и направлены снизу вверх.
Помещаем начало координат на левом конце, тогда u0 = 0. Для определения J0 используем условие, что при z = l прогиб равен нулю (u = 0)*:
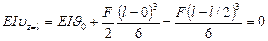
откуда 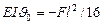
Следовательно, J = JA = Jmax = - 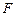
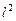 /(
/( 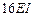 )
)
Ввиду симметрии угол поворота на правой опоре JВ = -JА = 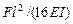 .
.
Максимальный прогиб umax = 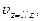
 следовательно,
следовательно,
* В данном случае можно было определить J0 также из условия, что посередине пролета касательная к упругой линии горизонтальна, т. е. 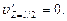
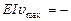
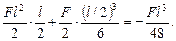
Окончательно
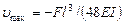 (вниз) (VII.29)
(вниз) (VII.29)
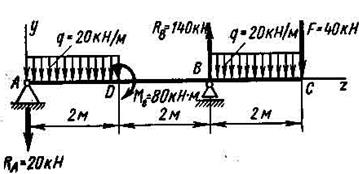 Пример VII.11. Определить прогибы в точках D и С и угол поворота в точке В балки, изображенной на рис. VII.15. Момент инерции сечения балки I =13 380 см4 = 13 380·10-8 м4 (двутавр № 36); E = 2·105 МПа.
Пример VII.11. Определить прогибы в точках D и С и угол поворота в точке В балки, изображенной на рис. VII.15. Момент инерции сечения балки I =13 380 см4 = 13 380·10-8 м4 (двутавр № 36); E = 2·105 МПа.
Р е ш е н и е. Определяем опорные реакции:
1. 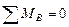 ;
; 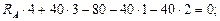
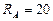 кН.
кН.
2. 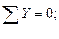
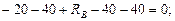
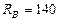 кН.
кН.
Помещаем начало координат на левой опоре. Тогда u0 = 0. Угол J0 определяем из условия, что при z = 4 м u = 0.
По универсальному уравнению для прогибов при z = 4 м имеем
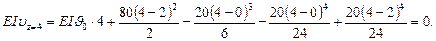
Так как распределенная нагрузка обрывается в точке D, то согласно сказанному ранее продолжаем ее до конца, но вводим компенсирующую нагрузку обратного направления на участке DВ. Последний член как раз и учитывает распределенную нагрузку, действующую снизу вверх (на чертеже указанные преобразования нагрузки не отражены).
Произведя вычисления, получаем 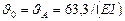 Определяем прогибы:
Определяем прогибы:
в точке С (z = 6 м)
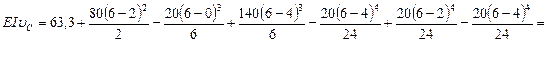
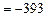 кН·м3 = -0,393 МН·м3;
кН·м3 = -0,393 МН·м3; 
в точке D
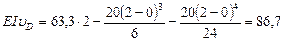 кН·м3 =
кН·м3 = 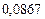 МН·м3.
МН·м3.
Окончательно получаем
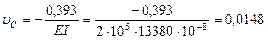 м =
м = 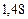 см.
см.
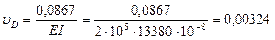 м =
м = 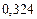 см.
см.
Определяем угол поворота в точке В. По универсальному уравнению для углов поворота при z = 4 м имеем
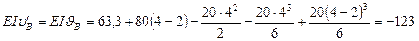 кНм2,
кНм2,
откуда 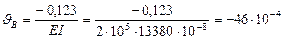 рад.
рад.
Дата добавления: 2016-06-05; просмотров: 2509;










