Совместная СЛАУ может иметь одно или несколько решений и называется
ОПРЕДЕЛЕНИЕ И МАТРИЧНАЯ ЗАПИСЬ (СЛАУ)
В этой главе будут рассмотрены линейные системы алгебраических уравнений. Эти СЛАУ появляются во многих областях прикладной математики. Например, при нахождении приближенных решений дифференциальных и интегральных уравнений, которые описывают различные процессы в физике, химии, биологии и экономике. Размерность СЛАУ, как правило, является большой и зависит от сложности решаемой проблемы. Так, в теории электрических сетей количество уравнений равно количеству ячеек сети и т.д.
В общем виде система линейных алгебраических уравнений с n неизвестными x1, x2, ..., xn записывается так:
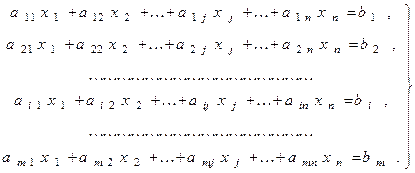 (1)
(1)
Коэффициенты при неизвестных 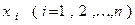 обозначаются через aij, где первый индекс i указывает номер уравнения, в котором находится данный коэффициент, а второй индекс j - номер неизвестного, при котором находится данный коэффициент.
обозначаются через aij, где первый индекс i указывает номер уравнения, в котором находится данный коэффициент, а второй индекс j - номер неизвестного, при котором находится данный коэффициент.
Например, коэффициент a45 находится в четвертом уравнении при неизвестном x5.
Числа b1, b2, ..., bm в системе (1) называются свободнымичленами в СЛАУ (1).
ОПРЕДЕЛЕНИЕ 1. Решением СЛАУ (1) называется любая совокупность чисел c1, c2, ..., cn, которая будучи подставленной на место неизвестных x1, x2, ..., xn в уравнения данной системы , обращает все эти уравнения в тождество.
ОПРЕДЕЛЕНИЕ 2.СЛАУ (1) называется совместной, если она имеет решение, и несовместной, если не имеет решения.
Совместная СЛАУ может иметь одно или несколько решений и называется
определенной, если имеет одно решение, и неопределенной, если имеет несколько решений.
ОПРЕДЕЛЕНИЕ 3.Две СЛАУ с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.
Так следующие элементарные преобразования переводят данную СЛАУ в эквивалентную:
а) перестановка двух уравнений системы;
б) умножение обеих частей уравнения системы на любое, отличное от нуля число;
в) прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число, отличное от нуля.
ОПРЕДЕЛЕНИЕ 4.СЛАУ, в которой все свободные члены b1, b2, ..., bn равны нулю называется однородной СЛАУ.
Матрицей A СЛАУ (1) называется матрица, составленная из коэффициентов при неизвестных этой системы
A= 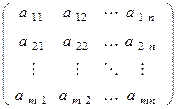 . (2)
. (2)
Используя понятие матрицы A СЛАУ (1) и матриц-столбцов, введенных соотношениями:
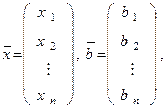 (3)
(3)
запишем систему (1) следующим образом
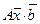 (4)
(4)
Из вида записи (4) следует, что первая компонента вектора 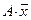 вычисляется как произведение первой строки матрицы A на вектор-столбец
вычисляется как произведение первой строки матрицы A на вектор-столбец 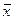 .
.
Приравнивая полученное выражение первой компоненте матрицы-столбца B, получим первое уравнение системы (1)
a11x1 + a12x2 + ... + a1nxn = b1
Второе уравнение СЛАУ (1) получается, если вторую строку матрицы A умножить на матрицу-столбец 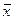 и приравнять полученное соотношение второму элементу матрицы
и приравнять полученное соотношение второму элементу матрицы 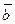 и т.д.
и т.д.
Пример. Записать в матричной форме следующую СЛАУ:
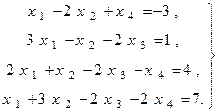
ÑМатрица A для этой системы имеет вид
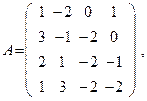
а матрицы-столбцы запишутся так
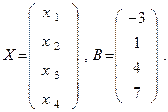
Тогда матричная запись исходной системы будет иметь вид
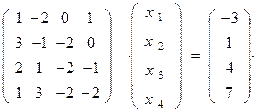
или
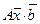
§2. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
Дата добавления: 2016-06-05; просмотров: 2282;










