Экпоненциал матрицы и формула Коши
Вспомним, что общее решение линейной системы
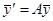 (1)
(1)
имеет вид 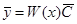 , где
, где 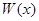 – фундаментальная матрица этой системы. Из теоремы 2 предыдущей лекции следует, что в случае различных собственных значений матрицы А фундаментальная матрица имеет вид
– фундаментальная матрица этой системы. Из теоремы 2 предыдущей лекции следует, что в случае различных собственных значений матрицы А фундаментальная матрица имеет вид
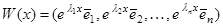 (2)
(2)
В общем случае фундаментальная матрица может быть найдена следующим образом. Подобно тому, как это делалось для уравнения первого порядка, для отыскания решения системы (1) , удовлетворяющего начальному условию 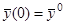 , применим метод последовательных приближений:
, применим метод последовательных приближений:
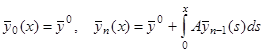 .
.
По индукции легко получить
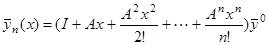 (3)
(3)
Введем в рассмотрение экспоненциал матрицы А:
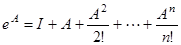 (4)
(4)
Можно показать, что матричный ряд (4) сходится для любой матрицы А. По аналогии с функцией 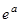 , матричная экспонента обладает свойствами:
, матричная экспонента обладает свойствами:
1) 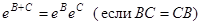
2) если 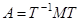 , то
, то 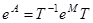 .
.
Из приведенных рассуждений следует, что вектор-функции (3) на любом отрезке 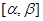 сходятся к вектору
сходятся к вектору 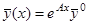 , являющемуся решением уравнения (1). Таким образом, матрица
, являющемуся решением уравнения (1). Таким образом, матрица 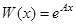 является для системы (1) фундаментальной матрицей и
является для системы (1) фундаментальной матрицей и 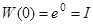 .
.
Отыскание экспоненциала матрицы в случае различных собственных значе- ний матрицы А.
Как отыскивать матрицу 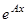 в этом случае, мы по сути дела, уже знаем. Для этого можно поступить, например, так: Найти собственные векторы
в этом случае, мы по сути дела, уже знаем. Для этого можно поступить, например, так: Найти собственные векторы 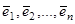 матрицы А и составить из столбцов их координат матрицу
матрицы А и составить из столбцов их координат матрицу 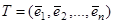 . Тогда
. Тогда
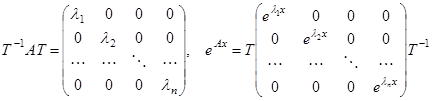 .
.
Если среди различных корней характеристического уравнения имеются комплексно-сопряженные, то следует найти общее решение системы (1) так, как это было описано выше, а потом искать 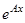 из следующих соображений: i-ым столбцом матрицы
из следующих соображений: i-ым столбцом матрицы 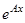 будет решение системы (1), удовлетворяющее начальным условиям
будет решение системы (1), удовлетворяющее начальным условиям 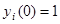 ,
, 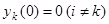 .
.
Проиллюстрируем изложенные методы нахождения экспоненциала матрицы на конкретных примерах.
Пример 1. Пусть матрица А такая же, как в примере 2 предыдущей лекции, то есть 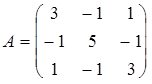 . Из координат столбцов собственных векторов этой матрицы составим матрицу Т, приводящую матрицу А к диагональному виду:
. Из координат столбцов собственных векторов этой матрицы составим матрицу Т, приводящую матрицу А к диагональному виду: 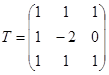 . Тогда
. Тогда
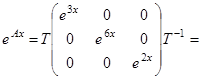
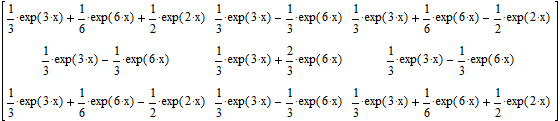
Пример 2 .Вернемся к системе, рассмотренной в примере 3 предыдущей лекции. Решение этой системы имеет вид
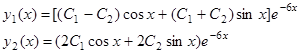 .
.
Найдем, сначала частное решение, удовлетворяющее условию 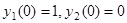 . Оно будет иметь вид
. Оно будет иметь вид
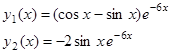 .
.
Частное решение, удовлетворяющее условиям 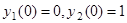 , имеет вид
, имеет вид
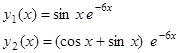 .
.
Поэтому
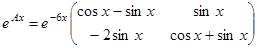 . (5)
. (5)
Дата добавления: 2022-05-27; просмотров: 79;










