Огибающая семейства интегральных кривых как особое решение.

Нахождение особых решений.

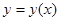Вспомним, что для нахождения кривых, подозрительных на особые решения, для уравнения, разрешенного относительно производной , мы искали кривые , вдоль которых не ограничена частная производная 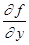. Предположим, что уравнение 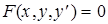определяет конечное или бесконечное число соотношений

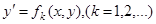причем все функции дифференцируемы по . Применяя к каждому из этих соотношений приведенные выше рассуждения, приходим к требованию:

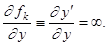(1)

Найдем 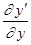непосредственно из уравнения 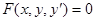. Для этого продифференцируем его по :

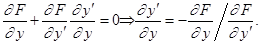
Ясно, что условие (1) выполнено, если

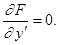(2)

Уравнение (2) необходимо рассматривать совместно с исходным дифференциальным уравнением:

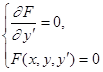(3)

Кривые, подозрительные на особые решения, могут быть найдены из системы (3) исключением 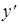. Пусть 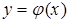– решение системы (3). Прежде чем утверждать, что найдено особое решение исходного уравнения, необходимо проверить, что:

1) 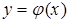– решение уравнения ,

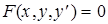2) 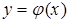– особое решение, то есть в каждой точке кривой 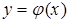ее касаются другие интегральные кривые того же уравнения.

Огибающая семейства интегральных кривых как особое решение.

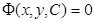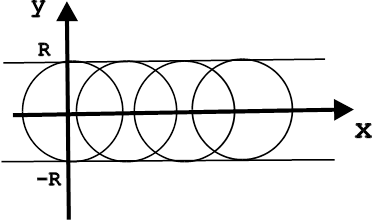
Пусть задано однопараметрическое семейство кривых . Кривая 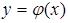называется огибающей для этого семейства, если в каждой своей точке она касается хотя бы одной кривой семейства и ни на каком участке не совпадает ни с одной кривой семейства. Так, например, для семейства окружностей

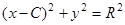огибающими будут прямые .

Очевидно, что огибающая семейства интегральных кривых дифференциального уравнения есть решение этого уравнения и притом особое.

Укажем (без доказательства) алгоритм нахождения огибающей семейства интегральных кривых дифференциального уравнения.

Для нахождения огибающей семейства интегральных кривых 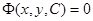следует исключить параметр С из системы уравнений

(4)

и проверить, является ли полученная кривая огибающей, то есть, касаются ли ее в каждой точке кривые данного семейства.

Пример нахождения особых решений уравнения, не разрешенного относительно производной, будет приведен ниже.

Рассмотрим теперь некоторые специальные классы уравнений не разрешенных относительно производной и методы их интегрирования.

1) Уравнение может быть разрешено относительно :

(5)

Введем обозначение 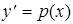. Тогда

.

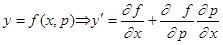Получили линейное уравнение относительно переменной р. Если найдено его решение , то 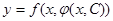– общее решение уравнения (5).

Пример. Уравнение 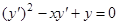может быть разрешено относительно

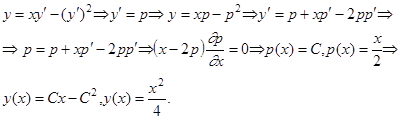
Легко проверить, что через точку , принадлежащую области существования решения, проходят две различные интегральные кривые:

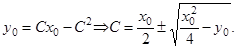
Попытаемся найти особое решение данного уравнения. Для этого запишем систему (3)

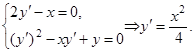
Проверим, что 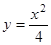– особое решение. То, что эта функция является решением уже показано выше. Запишем условия касания интегральных кривых 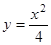и 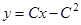в точке :

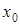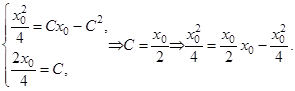
Получили верное равенство. Значит 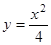– особое решение.

Найдем теперь огибающую семейства 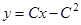. Для этого запишем систему (4)

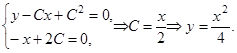
Итак, 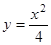– особое решение, являющееся огибающей.

2) Уравнение может быть разрешено относительно х: 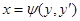. В этом случае уравнение может быть решено с использованием подстановки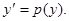

Пример. Найти общее решение уравнения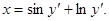

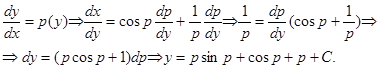
Итак, параметрические уравнения решения имеют вид

Дата добавления: 2022-05-27; просмотров: 204;

Поиск по сайту