Определение и свойства определенного интеграла. Формула Ньютона – Лейбница.
Построение понятия определенного интеграла состоит из следующих этапов.
Пусть на отрезке [a, b] определена функция у = f(x). Отрезок [a, b] разобьем на п частей точками а = х0 < х1 < х2 < ….. < х < хп = b (разбиение R). На любом отрезке( 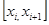 - частичный отрезок) выберем по произвольной точке ξ
- частичный отрезок) выберем по произвольной точке ξ 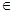 [х
[х 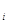 , xi+1]. (Рис1) ∆х
, xi+1]. (Рис1) ∆х 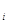 =х
=х 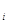 +1-х
+1-х 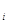 - длина отрезка. Составим сумму S
- длина отрезка. Составим сумму S 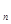 =
= 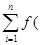 ξ
ξ 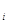 )∆х
)∆х 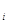 - n – ая интегральная сумма (Римана) функции f на отрезке [a, b].
- n – ая интегральная сумма (Римана) функции f на отрезке [a, b].
 Геометрический смысл суммыSn - это есть алгебраическая сумма площадей
Геометрический смысл суммыSn - это есть алгебраическая сумма площадей
прямоугольников, в основании которых лежат отрезки ∆x 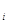 , a
, a
высоты равны f(ξ 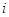 ). (В том
). (В том
случае функция неотрицательна функция)
Обозначим через γR = max ∆x 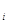 - максимальную длину отрезков
- максимальную длину отрезков
длину отрезков [х 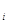 х
х 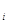 +1] разбиения R. Предел (если он существует), к которому стремится интегральная сумма рис1. Sn, когда γR = max ∆x
+1] разбиения R. Предел (если он существует), к которому стремится интегральная сумма рис1. Sn, когда γR = max ∆x  →0, называется определенным интегралом от функции f на отрезке [a, b] и обозначается:
→0, называется определенным интегралом от функции f на отрезке [a, b] и обозначается:
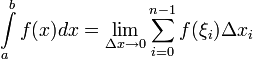 |
(1)
Предел (1) называют интегралом Римана и функцию, для которой этот предел существует называют интегрируемой в смысле Римана.
Определение:Определенным интегралом функции у= 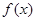 на отрезке
на отрезке 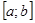 называется интеграл:
называется интеграл: 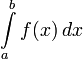
a – нижний предел.
b – верхний предел.
f(x) – подынтегральная функция.
dx- дифференциал независимой переменной.
Непосредственное вычисление определенного интеграла по формуле (1) связано с рядом трудностей, так как интегральные суммы имеют сложный вид, и найти их предел нелегко. До XVII века вычисление интегралов являлось трудной математической задачей. Ньютон и Лейбниц указали метод решения таких задач путем сведения к отысканию первообразной функции.
Таким образом, определенный интеграл вычисляется с помощью фундаментальной формулы Ньютона – Лейбница:
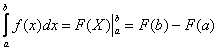 |
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:
1) Постоянный множитель можно выносить за знак интеграла :
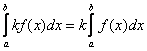 |
Интеграл от алгебраической суммы равен сумме интегралов от этих функций:
2) Для любых чисел a, b и с имеет место равенство:
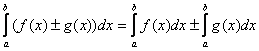 | ||
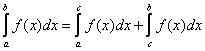 |
4) При перемене местами пределов интегрирования интеграл изменяет лишь знак:
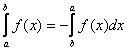
5) 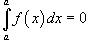
2. Вычисление определенных интегралов различными методами.
1. Непосредственное интегрирование - вычисление интегралов с помощью
непосредственного использования таблицы простейших интегралов, основных свойств
неопределенных интегралов и формулы Ньютона – Лейбница.
2. Замена переменной в определенном интеграле:
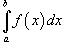 |
Определенный интеграл
по переменной x можно преобразовать в определенный интеграл относительно переменной
t с помощью подстановки x = g (t):
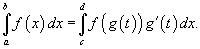
Новые пределы интегрирования по переменной t определяются выражениями
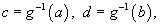 |
где g 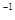 - обратная функция к g, т.е. t = g
- обратная функция к g, т.е. t = g 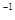 (x).
(x).
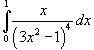 |
Пример1:
Решение.
Сделаем замену:
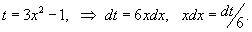
Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то
t = 2. Тогда интеграл через новую переменную t легко вычисляется:
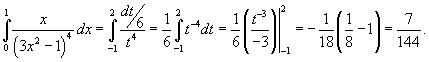 |
- Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:
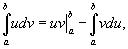 |
Где u и v – непрерывно дифференцируемые функции от х. С помощью этой формулы
нахождение интеграла 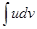 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 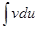
При этом за u берется такая функция, которая при дифференцировании упрощается,
за dv – та часть подынтегрального выражения, интеграл от которой известен или
может быть найден.
Пример 2:
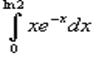 |
Вычислить интеграл
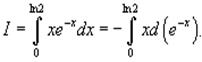 |
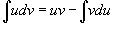 Используем интегрирование по частям: В нашем случае пусть будет
Используем интегрирование по частям: В нашем случае пусть будет
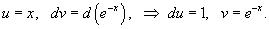 |
Следовательно, интеграл равен
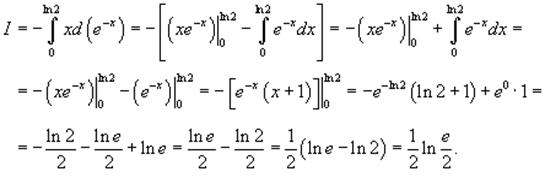 |
3. Применение определенного интеграла к вычислению площади плоской фигуры,
Объемов тел.
Фигура, ограниченная на плоскости ОХУ отрезком  оси ОХ, прямыми х=a, x=b и
оси ОХ, прямыми х=a, x=b и
графиком непрерывной и неотрицательной функции у = f(x) на [a,b], называется
криволинейной трапецией.
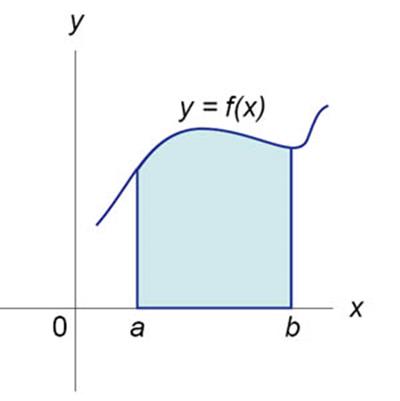
Площадь криволинейной трапеции вычисляется с помощью определенного интеграла:
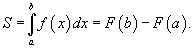
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно.
Если f (x) ≥ g (x) на замкнутом интервале [a, b],
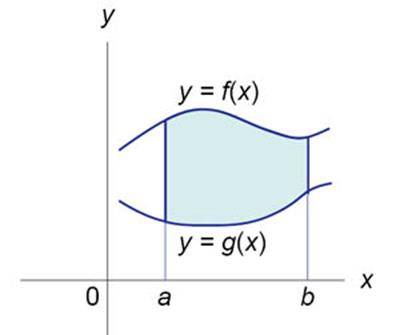
то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными
линиями x = a, x = b (рисунок 2), определяется формулой
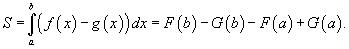
Вычисление объемов тел вращения:
Пусть дана кривая у=f(x), a≤x≤b. Объем тела вращения, ограниченного плоскостями х= a и х=b и поверхностью вращения кривой вокруг оси ОХ вычисляется по формуле:
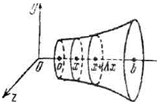
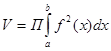
Аналогично можно получить формулу объема тела вращения вокруг оси ОУ
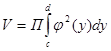 ;
;
Длина дуги кривой вычисляется по формуле:
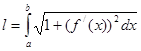
Если площадь сечения тела плоскостью, перпендикулярной оси Ох, выражена как функция
от х, т.е. в виде Ѕ = Ѕ(х) (а 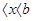 ), то объем части тела, заключенный между перпендикулярными
), то объем части тела, заключенный между перпендикулярными
оси Ох плоскостями х=а и х=b находится по формуле
V= 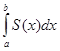
| <== предыдущая лекция | | | следующая лекция ==> |
| Некоторые генетико-популяционные, демографические и экологические понятия. | | |
Дата добавления: 2022-05-27; просмотров: 67;










