Задачи линейного программирования (ЛП).
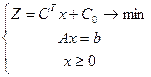
| - стандартная форма задачи ЛП |
 В общем случае, если
В общем случае, если 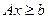 , то допустимая область представляющая собой многогранник в пространстве.
, то допустимая область представляющая собой многогранник в пространстве.
В случае  - многогранник, имеющий неполную размерность.
- многогранник, имеющий неполную размерность.
Допустим, имеется некоторое выпуклое множество. Тогда в любой граничной точке этого множества, всегда можно провести опорную гиперплоскость, т.е. такую гиперплоскость которая имеет с множеством только одну общую точку, и все множество находится по одну сторону от гиперплоскости.
 |
Если –grad является нормалью к гиперплоскости и плоскость не опорная, то можно двигаться под острым углом к –grad, тем самым улучшая значение функции. Такое движение невозможно, если антиградиент определяет опорную плоскость. Следовательно в этом случае это точка локального минимума, который является и глобальным.
Геометрически, чтобы найти точку локального минимума, необходимо найти такую вершину глобального множества, что плоскость которая является нормальной к антиградиенту является опорной.
Рассмотрим  , т – ограничений равенств, п – число переменных.
, т – ограничений равенств, п – число переменных.
n
 |
m A
Первые m столбцов линейно независимы. 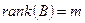 ,
,  .
.
n n-m

A = B N m
Базисная матрица
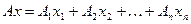 ,
, 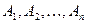 - столбцы матрицы
- столбцы матрицы
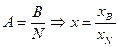 - базисные переменные
- базисные переменные
Тогда систему ограничений равенств можно записать
 ;
;
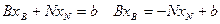 ;
;
Для В существует обратная матрица 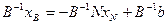 ;
;

Если для данного базиса зафиксируем не базисные переменные в нуле, то получим точку, которая является вершиной многогранника.
Вершины многогранника множества характеризуемые тем, что небазисные переменные равны 0.
Что делать если вершина не точка оптимума.
Рассмотрим целевую функцию:
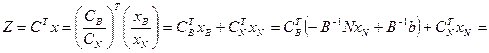
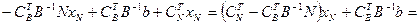

d – показывает суммарное влияние небазисных переменных на целевую функцию
d0 – множители Лагранжа или относительные оценки небазисных переменных.

Z
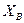
Точка будет точкой оптимума, если все 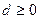 .
.
Если имеется один отрицательный коэффициент.
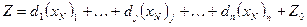
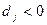 следовательно можно увеличить
следовательно можно увеличить 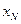 , тогда целевая функция начнет улучшаться.
, тогда целевая функция начнет улучшаться.
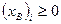 , если
, если 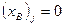 , то дальше
, то дальше 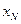 увеличивать нельзя
увеличивать нельзя 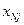 и
и 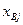 меняются местами.
меняются местами.
Дата добавления: 2022-05-27; просмотров: 125;










