Общая характеристика нелинейных систем

Основная особенность нелинейных систем заключается в том, что они не удовлетворяют принципу суперпозиции. Математические модели нелинейных систем – это системы нелинейных дифференциальных или алгебраических уравнений. Эти модели также делятся на модели вход-выход и модели в переменных состояния. Модель вход-выход может иметь, например, вид:

, (9.1)

где 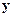, , 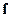– векторы выходных величин, входных задающих воздействий и возмущений; 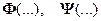– нелинейные вектор-функции. Модели нелинейных систем в переменных состояния в общем случае – это система уравнений вида:

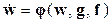, (9.2)

, (9.3)

где 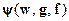– некоторые нелинейные вектор-функции. Вектор переменных состояния здесь обозначен , так как в исходных уравнениях нелинейных систем всегда фигурируют не отклонения переменных, вектор которых выше обозначался как 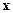, а вектор самих переменных состояния рассматриваемой системы.

Обычно в нелинейных системах можно выделить ряд линейных и ряд существенно нелинейных элементов. Деление на линейные и нелинейные элементы или системы достаточно условно. Обычно под существенно нелинейными элементами или системами понимают такие, которые при сформулированных требованиях к точности их описания не могут быть описаны линейными дифференциальными или алгебраическими уравнениями. Если в этих условиях некоторый элемент может быть описан линейной моделью, то он называется линейным. Возможность описания системы линейной или нелинейной моделью связана либо с величиной отклонений переменных системы от их установившихся значений, либо с не дифференцируемостью (не гладкостью) нелинейных характеристик её элементов.

Так как нелинейности могут быть весьма сложного вида, то нелинейная система в общем случае может иметь несколько положений равновесия. Поэтому понятие устойчивости системы в случае нелинейных систем трансформируется в понятие устойчивости положений равновесия. При этом разные положения равновесия одной и той же системы могут иметь разный характер по устойчивости. В связи с этим в теории нелинейных систем вводятся понятия устойчивости в малом, устойчивости в большом, устойчивости в целом и ряд других понятий устойчивости.

Существенным фактом является то, что многие нелинейные системы являются работоспособными и при наличии неустойчивых положений равновесия, а некоторые нелинейные системы работоспособны только при таких положениях равновесия. Нелинейные системы в установившемся режиме могут совершать периодические и хаотические (типа случайных колебаний) движения. Хаотические движения нелинейных систем характеризуются тем, что они ограничены по амплитуде, но никогда не повторяются и не затухают.

Для примера на рис. 9.1 приведены графики изменения отклонений 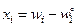, переменных w₁(t) (рис. 9.1,а) и w₃(t) (рис. 9.1,б) системы уравнений Рёсслера:

, , .

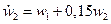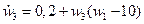от её положения равновесия 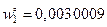, , 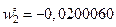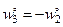. Эти колебания соответствуют следующим начальным условия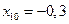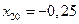м: , и . Хорошо видно, что, во-первых, возникающие в системе Рёсслера колебания не являются периодическими. Интервалы возрастания и убывания переменных здесь чередуются, но всё время меняются как по длительности, так и по амплитуде. Во-вторых, характер изменения переменных w₁(t) и w₃(t) совершенно различен, что не характерно для обычных нелинейных систем. Именно поэтому, движения систем, соответствующие таким изменениям переменных, и сами системы называются хаотическими.

Из-за сложности нелинейных дифференциальных уравнений в настоящее время нет единого метода анализа нелинейных динамических систем. Теория нелинейных систем управления в настоящее время – это совокупность методов анализа и синтеза, каждый из которых разработан применительно к некоторому классу нелинейных систем.