Синтез робастных систем управления

Системы данного типа, в отличие от рассмотренных выше, состоят из линейного объекта управления с неопределённостью (см. § 4.6) и линейного регулятора. Соответствующие H^∞-оптимальные регуляторы, помимо робастной устойчивости замкнутой системы (см. § 4.6), обеспечивают подавление влияния внешних воздействий на ошибку системы в заданной степени и оптимизацию других критериев качества управления при наличии неопределённости в объекте. При этом воздействия также предполагаются ограниченными, но в известной степени неопределёнными.

Строгие методы теории H^∞-оптимизации являются аналитическими, причём для их реализации разработаны специальные программные средства, например, они имеются в системе MATLAB. Однако непосредственное применение этих методов осложнено рядом трудностей. Во-первых, необходимо задать ряд вспомогательных функций, выбор которых достаточно сложен. Во-вторых, порядок H^∞-оптимальных регуляторов часто получается значительно выше порядка объекта управления. Наконец, робастные к параметрам объекта системы оказываются не грубыми к параметрам самого H^∞-оптимального регулятора. Поэтому целесообразнее осуществлять синтез оптимальных в смысле H^∞-критерия робастных САУ с априори выбранным регулятором, небольшого порядка. Именно этот подход к построению робастных САУ рассматривается ниже.

В настоящее время синтез H^∞-оптимальных регуляторов ведется либо на основе передаточных функций (передаточных матриц в многомерном случае), либо на основе уравнений в переменных состояния объекта управления с неопределенностями.

Рассмотрим определение систем, оптимальных в смысле H^∞-критерия, в терминах передаточных функций, ограничившись случаем одномерных систем (с одним входом и одним выходом). Схема рассматриваемой здесь САУ соответствует рис. 1.1. Объект управления может описываться передаточной функцией следующего вида:

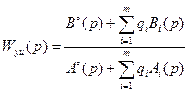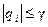, , (8.45)

где 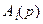, 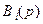– заданные полиномы, 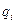– неопределённые параметры, 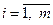; 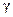– масштаб параметрической неопределённости объекта.

Передаточная функция 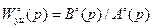соответствует номинальному объекту. Объект с неопределённостью может быть задан и непараметрической передаточной функцией вида

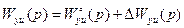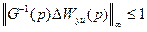, , (8.46)

Здесь 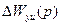– неопределённая рациональная функция, описывающая аддитивную неопределённость объекта управления; 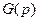– вспомогательная (весовая) функция. Выбором этой функции можно изменять частотный диапазон неопределенностей ОУ, влияние которых должно подавляться проектируемым H^∞-оптимальным регулятором робастной САУ.

Отметим, что в (8.46) и далее через 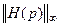обозначается H^∞-норма функции H(p). Эта норма определяется выражением

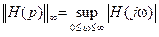, (8.47)

т.е. H^∞-норма некоторой функции H(jω) представляет собой sup – точное верхнее значение

модуля этой функции H(jω), определённое по всем частотам от нуля до бесконечности.

H^∞-оптимальный регулятор, прежде всего, является стабилизирующим и в рассматриваемом случае описывается передаточной функцией 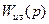, т.е. он реализует управление по отклонению (по выходу, если задающее воздействие g равно нулю).

Как отмечалось выше, аналитическое определение структуры и параметров H^∞-оптимального регулятора нерационально. Поэтому чаще всего структурой его задаются, а параметры определяются в процессе синтеза путем параметрической оптимизации. Например, это может быть П-регулятор

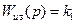, (8.48)

или ПИ-регулятор

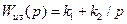, (8.49)

или ПИД-регулятор

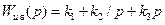, (8.50)

или регулятор 1-го порядка

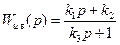. (8.51)

Здесь k₁, k₂, k₃ – искомые параметры регуляторов (8.48) – (8.51).

Кроме устойчивости, H^∞-оптимальный регулятор должен обеспечить оптимальное значение некоторого критерия качества замкнутой системы. Чаще всего используется H^∞-критерий, который формулируется следующим образом:

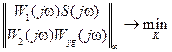, (8.52)

где W₁(p), W₂(p) – вспомогательные весовые функции, назначение которых то же, что и функции 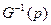в (8.46); S(p) – функция чувствительности системы. Эта функция в рассматриваемом случае определяется выражением

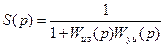. (8.53)

Функция W_yg(p) в (8.52) – это передаточная функция замкнутой системы

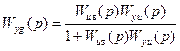. (8.54)

Физический смысл H^∞-критерия (8.52) заключается в следующем. Как показано в главе 5, ошибка системы, вызванная внешними воздействиями, определяется выражением

,

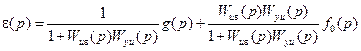где g(p) – изображение задающего воздействия; f₀(p) – изображение возмущающего воздействия, приложенного (или приведённого) к входу системы.

Регулятор системы всегда выбирается так, чтобы при номинальных значениях параметров система имела требуемые показатели качества. При любых изменениях свойств объекта управления или воздействий ошибка системы, естественно, изменяется. В качественной системе эти изменения должны быть, естественно, минимальными.

Допустим, свойства объекта управления, а также задающего и возмущающих воздействий изменились так, что их изображения имеют вид, аналогичный (8.46), т.е. 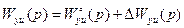, , 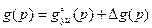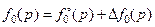. Тогда для модуля изменения ошибки можно записать равенство

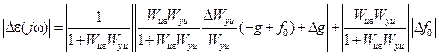. (8.55)

В правой части равенства (8.55) аргумент jω всех функций опущен для краткости. С учетом обозначений (8.53) и (8.54) равенство (8.55) можно представить так

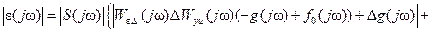
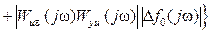. (8.56)

Здесь

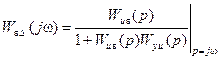(8.57)

функция чувствительности системы к изменениям свойств объекта управления.

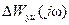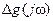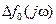Согласно (8.56), влияние изменений объекта, которые описываются функцией , а также изменения задающего и возмущающего воздействий ( и ) определяются, очевидно, значениями функций 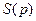(8.53) и 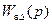(8.57) или, что то же самое, значениями функци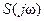й , и 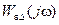. Именно поэтому эти функции и называются функциями чувствительности.

В соответствии с выражением (8.56), чем меньше будут максимальные значения модулей функци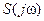й и 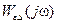, тем меньше будет влияние изменений свойств объекта и внешних воздействий на свойства замкнутой системы, т.е. тем более робастной она будет.

Чтобы учесть в H^∞-критерии те или иные (высоко- или низко-) частотные составляющие воздействий, вводятся весовые вспомогательные функци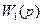и и 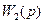. Ясно, что в критерии (8.52) будут учитываться составляющие воздействий лишь с теми частотами, на которых функци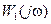и и 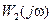существенно отличаются от нуля. Примеры этих функций приводятся ниже.

Обозначим передаточную функцию H^∞-регулятора, имеющего некоторое число параметров k_i через 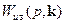, где 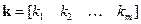– m-вектор строка параметров.

На практике H^∞-регулятор обычно определяется путем решения следующих более

простых задач:

1. Обеспечение робастной устойчивости при аддитивной неопределенности (8.46). В этом случае H^∞-критерий (8.52) переходит в критерий

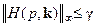, (8.58)

где

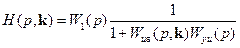(8.59)

или

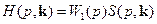. (8.60)

2. Обеспечение H^∞-качества. Здесь H^∞-критерий (8.52) с учетом (8.54) переходит в критерий

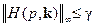, (8.61)

где

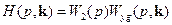(8.62)

Применяются и другие представления H^∞-критерия (8.52), которые позволяют минимизировать влияние различных неопределённостей системы управления.

Фактически, в случае задач 1 или 2 H^∞-оптимальный регулятор должен обеспечить следующие свойства:

а) замкнутая система является устойчивой, т.е. её характеристический полином

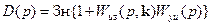(8.63)

удовлетворяет критерию Гурвица;

б) функция H(p, k) (8.62) также соответствует устойчивой системе;

в) для заданного числа γ выполняется неравенство

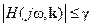, при всех .

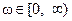Из условия а) следует, очевидно, что объект управления при всех изменениях его

структуры и параметров должен быть стабилизируемым. В противном случае задача синтеза H^∞-оптимального регулятора решения не имеет.

Если объект является стабилизируемым [см. С. 68], то искомый H^∞-оптимальный регулятор можно найти следующим образом. Сначала в пространстве параметров k_i строятся области, в каждой из которых выполняется одно из условий а), б) или в). Затем находится пересечение указанных областей, что и определяет область, любая точка которой соответствует параметрам искомого H^∞-оптимального регулятора. Конкретные значения параметров регулятора выбираются, исходя из дополнительных соображений, например, по времени регулирования, перерегулированию, колебательности и т.п. (см. далее, пример 8.4).

Если весовые функции W₁(p) и W₂(p) устойчивы, то условия а) и б) совпадают. Имея это в виду, представим функцию H(p, k) (8.62) следующим образом:

.

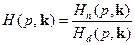Тогда граница области в пространстве параметров, где выполняются условия а) и б) определяется [6] решением системы уравнений

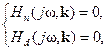
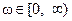, (8.64)

Граница области, где выполняется условие в) определяется решением следующей системы из трёх уравнений:

, ,

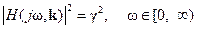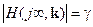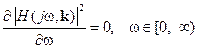. (8.65)

Системы (8.64) и (8.65) в общем случае решаются с применением ЭВМ. Однако в некоторых случаях можно получить и аналитическое решение.

Например, для ПИД-регулятора (8.50) 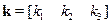, поэтому при фиксированном k₁, когда замкнутая система должна удовлетворять критерию (8.61), (8.62), функция

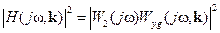. В этом случае система (8.65) имеет вид:

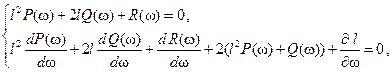(8.66)

где

,

, ,

.

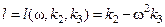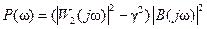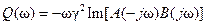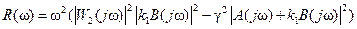В этих выражениях B(jω) и A(jω) – числитель и знаменатель комплексного коэффициента передачи объекта управления, т.е.

.

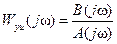Вещественные корни первого уравнения (8.66)

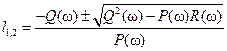(8.67)

существуют только при условии 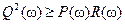, которое позволяет выделить интервалы частот, в которых следует искать решение системы (8.66). Из второго уравнения (8.66) находится выражение для k₃(ω), а затем – для k₂(ω) = l + ω² k₃(ω). В результате получаются параметрические выражения для координат точек двух кривых, которые определяют область допустимых значений параметров регулятора

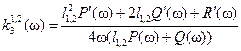, (8.68)

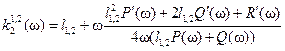. (8.69)

Здесь 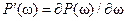, , 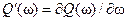а частота ω пробегает все те интервалы частот, в которых выполняется условие .

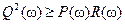Аналогично выписывается в явном виде и система (8.64). При этом, если полиномы числителей и знаменателей весовой функции W₂(jω) и комплексного коэффициента передачи объекта W_yu(jω) не имеют чисто мнимых (включая нуль) корней, то решением системы (8.64) является плоскость k₂ = 0 при ω = 0.

Пример 8.4. Найти параметры ПИД-регулятора (8.50) с k₁ = – 0,35, который обеспечивает H^∞-качество по критерию (8.61) при γ = 1 [6]. Передаточная функция объекта управления и вспомогательная весовая функция имеют вид

, .

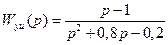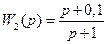Критерий (8.61) при заданной весовой функции W₂(p) обеспечивает малые значения передаточной функции системы на высоких частотах. Это обусловлено тем, что на малых частотах модуль 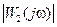близок к 0,1, а на высоких частотах – к единице.

Решение. В данном случае область устойчивости в плоскости (k₂, k₃) является треугольником с вершинами в точках (0; 0,4507), (0; – 1), (– 0,15; – 1). Этот треугольник показан на рис. 8.5. При γ = 1 из условия 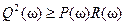следует уравнение

.

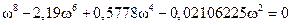Решение этого уравнения даёт два интервала частот: [0,2085; 0,50627] и [1,3749; ∞), в которых следует искать границы области допустимых параметров.

Выражения (8.68), (8.69) при различных значениях частот из указанных интервалов дают левую и нижнюю границы области допустимых параметров искомого ПИД-регулятора. Эта область располагается, естественно, внутри указанного выше треугольника и показана на рис. 8.5 штриховкой.

Переходные процессы системы при k₂ = – 0,02 и k₃ = – 0,4 приведены на рис. 8.6,а; а при k₂ = – 0,01 и k₃ = – 0,2 – на рис. 8.6,б соответственно. Как видно, характер переходных процессов H^∞-оптимальной системы существенно зависит от параметров регулятора. ■

Пример 8.5. Для объекта с передаточной функцией

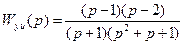(8.70)

найти H^∞-оптимальный регулятор, обеспечивающий низкую чувствительность замкнутой системы на низких частотах. Другими словами, регулятор должен обеспечить выполнение неравенства

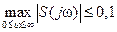, (8.71)

где S(jω) = S(p) при p = jω, а функция S(p) определяется выражениями (8.53), (8.70).

Решение. Теория H^∞-оптимизации не позволяет оптимизировать непосредственно функцию S(jω), поэтому для решения задачи синтеза формируется H^∞-критерий качества (8.52), где

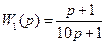, а 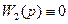. (8.72)

В результате минимизации критерия (8.52) с функциями (8.72) и (8.70) методом H^∞-оптимизации получается [10] следующее выражение для передаточной функции регулятора:

.

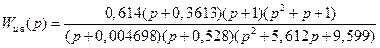При этом значение H^∞-критерия равно 0,1202.

Решение данной задачи можно получить с помощью более простого ПИ-регулятора с передаточной функцией

.

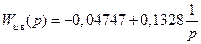При этом регуляторе значение H^∞-критерия равно 0,0373.

Как видно, более простой оптимальный ПИ-регулятор обеспечивает более высокое качество, чем сложный H^∞-оптимальный регулятор. Этим, в частности, можно объяснить широкое распространение типовых регуляторов (8.48) – (8.50) на практике.

Отметим также, что более высокое качество H^∞-оптимального ПИ-регулятора объясняется, во-первых, тем, что он имеет более простую структуру, а во-вторых, тем, что его параметры найдены путем непосредственной минимизации левой части неравенства (8.71) по параметрам регулятора (8.49).

Переходной процесс замкнутой системы с найденным H^∞-оптимальным ПИ-регулятором приведён на рис. 8.7. Как видно, несмотря на то, что она является оптимальной в смысле H^∞-нормы своей функции чувствительности, колебательность её переходных процессов, очевидно, слишком высока для практических применений. ■

Пример 8.6. Найти робастно стабилизирующий регулятор для объекта с интервальной передаточной функцией

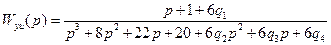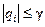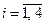, , . (8.73)

При γ = 1 эту функцию в более наглядной форме можно представит следующим образом:

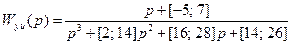. (8.74)

Решение. В результате применения техники H^∞-оптимизации при W_yu(p) (8.74) можно получить [10] робастно стабилизирующий регулятор с передаточной функцией

.

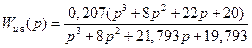С другой стороны, легко убедиться с помощью критерия Харитонова (см. § 4.6), что робастно стабилизирующим регулятором в данном случае является и простой П-регулятор (8.48) с коэффициентом передачи k₁ = 1. Причём, и в этом случае значительно более простой регулятор обеспечивает решение задачи робастной стабилизации неопределённого объекта. Более того, если применить более сложный робастно стабилизирующий регулятор, например, H^∞-оптимальный регулятор первого порядка типа (8.51) при k₁ = 1 и принять, что в передаточной функции (8.73) все величины 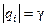, то, осуществляя прямую максимизацию величины γ по параметрам k₂ и k₃, получим робастно стабилизирующий регулятор с передаточной функцией

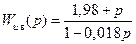. (8.75)

При этом величины q_i в неравенствах (8.73) могут удовлетворять неравенствам 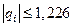, 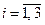. Следовательно, допустимую неопределённость объекта (8.73) можно значительно повысить, применяя простой регулятор первого порядка (8.75). Переходные процессы замкнутой системы (8.73), (8.75) при q₁ = – 0.666; q₂ = q₃ = q₄ = – 0,833 приведены на рис. 8.8,а, а при q₁ = q₄ = 1; q₂ = q₃ = –1 показаны на рис. 8.8,б.

С помощью критерия Харитонова также легко убедиться, что система (8.73), (8.75) остаётся устойчивой и при других значениях параметров объекта (8.73), где 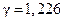. Однако характер её переходных процессов достаточно сильно отличается от переходного процесса при номинальных значениях параметров объекта управления. ■

Таким образом, параметрическая оптимизация H^∞-критериев при использовании простейших регуляторов типа (8.48) – (8.51) позволяет получать решение различных задач синтеза линейных САУ, если уравнения объектов содержат существенные неопределённости.

Отметим также, что понятие радиуса запасов устойчивости (см. § 4.5) позволяет синтезировать робастно устойчивые многомерные системы с заданным радиусом запасов устойчивости r* аналитическим методом [16]. При этом задача синтеза сводится к решению двух уравнений Риккати, для решения которых, как отмечалось выше, существуют специальные машинные программы.

Однако в этом случае допустимые вариации параметров и структуры объекта управления непосредственно, например, в виде (8.45) или (8.46), не оцениваются. Предполагается лишь, что отклонения параметров объекта и регулятора настолько малы, что выполняется неравенство (4.26) при некотором заданном значении r = r*.

Г л а в а 9