Синтез систем при минимально-фазовом объекте

Понижение степени знаменателя передаточных функций систем управления, синтез которых рассматривался в предыдущем разделе, происходит за счет компенсации части нулей характеристического полинома 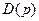(8.18) замкнутой системы. Это достигается путем формирования вспомогательного полинома 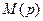, который должен удовлетворять условиям Гурвица. С другой стороны, этот полином не влияетна передаточные функции замкнутой системы и, следовательно, может иметь произвольные нули, лишь бы они располагались в левой части комплексной плоскости.

Если полином 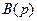числителя передаточной функции объекта по управлению имеет нули, расположенные на комплексной плоскости слева от мнимой оси, т.е. объект является минимально-фазовым, то компенсируемые нули полинома 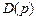целесообразно выбрать равными всем или части нулей полинома 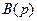. В этом случае понижение степени знаменателей передаточных функций системы управления будет происходить без потери свойства назначаемости коэффициентов их числителей.

С другой стороны, в этом случае часть полюсов замкнутой системы будут совпадать (будут согласованы) с нулями передаточной функции объекта. Такие системы называются САУ с согласованными полюсами.

Методика синтеза САУ с согласованными полюсами для минимально-фазовых объектов рассматривается в этом разделе. Заметим, что проверить минимально-фазовость заданного объекта (7.1), (7.2) очень легко. Для этого достаточно убедиться, что полином 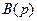из уравнения (7.24) удовлетворяет критерию Гурвица или Рауса (см. § 4.3).

Таким образом, для синтеза САУ с согласованными полюсами при минимально-фазовом объекте полином 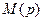в равенствах (8.18) – (8.20) можно принять

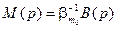. (8.24)

Тогда, согласно (8.18), полином

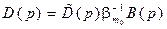, (8.25)

где 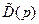– полином степени .

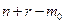Из равенства (8.6) следует, что данную структуру полинома 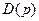можно обеспечить при условии, что

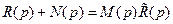, (8.26)

где

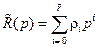(8.27)

полином, порядка 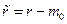коэффициенты которого 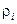, 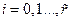определяются в процессе синтеза устройства управления.

Так как степень полинома – число всегда положительное или нуль, то на выбор порядка УУ, т.е. величины , накладывается наряду с условием (8.12) дополнительное условие

.

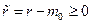Объединяя эти условия, получаем следующие формулы для определения величин и :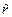

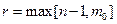, (8.28)

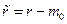. (8.29)

С учетом равенств (8.24) – (8.26) соотношение (8.6) принимает вид

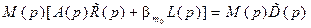
что эквивалентно полиномиальному уравнению

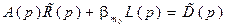. (8.30)

Здесь коэффициенты полинома 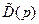степени 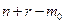по-прежнему задаются совместно с коэффициентами числителя передаточной функции (8.9), исходя из требований к качеству синтезируемой системы. Коэффициенты полиномов 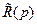степен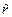и и степени определяются решением системы алгебраических уравнений, соответствующей этому полиномиальному уравнению.

В данном случае систему (8.16), эквивалентную уравнению (8.30), можно разрешить

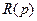в явной форме. Вытекающие из нее рекуррентные формулы для вычисления коэффициентов полиномов и при 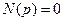в общем случае зависят от соотношения величин 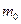и .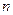

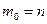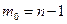I. Если или , то 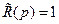, а коэффициенты

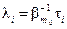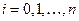, , (8.31)

где 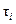– коэффициенты полинома

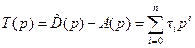. (8.32)

II. Если 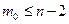, то полином 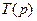определяется выражением

,

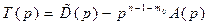а коэффициенты 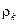полинома 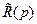(8.27) – рекуррентными формулами:

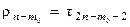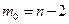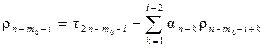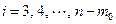при ,

, при .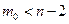

Полином 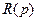вычисляется по формуле (8.26) при .

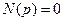Вприведенных выше формулах 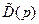– полином степени 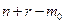, являющийся знаменателем вырожденных передаточных функций (8.9) и (8.10) замкнутой системы. Его

коэффициенты назначаются, исходя из требований к качеству синтезируемой системы.

Коэффициенты 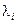полинома находятся по формулам

, ,

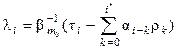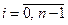где

,

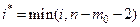а коэффициенты полинома 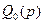– по формулам

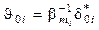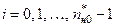, , (8.33)

где 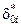– назначаемые коэффициенты числителя вырожденной передаточной функции (8.9) синтезируемой системы по задающему воздействию; 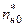– их число, причем .

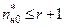Коэффициенты полинома определяются по формулам

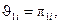
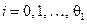, (8.34)

где 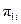– коэффициенты полинома

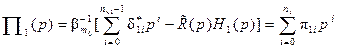(8.35)

Здесь 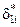, 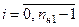– назначаемые коэффициенты числителя также вырожденной передаточной функции (8.10) системы по измеряемому возмущению 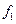; 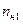– число этих коэффициентов.

Коэффициенты уравнений УУ в форме (8.1), (8.2) вычисляются по формулам (8.17) при условиях: 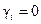, 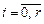. При назначении коэффициентов передаточных функций систем управления минимально-фазовыми объектами необходимо иметь в виду, что в данном случае полином их знаменателей имеет степень 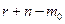. Степень числителя передаточной функции по задающему воздействию равна 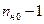, и все его коэффициенты назначаются.

Если доступных измерению возмущений 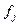несколько, т.е. 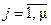, то коэффициенты соответствующих полиномам 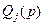векторов 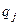и числа 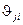определяются соотношениями (8.34), (8.35) и (8.17). Причем в первых двух соотношениях индекс 1 заменяется на 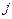. При этом степень числителя передаточной функции системы по возмущению 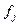равна .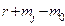

В соответствии с выражениями (8.13), (8.14) число назначаемых коэффициентов каж-

дого из этих числителей не больше 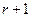, а число не назначаемых коэффициентов равно 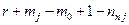и не меньше разности 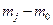. Следовательно, все коэффициенты 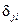числителя вырожденной передаточной функции по возмущению 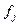системы управления минимально-фазовым объектом могут быть назначены только в том случае, когда

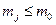. (8.36)

При этом условии коэффициенты 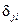целесообразно назначать, исходя из условий равенства нулю соответствующих коэффициентов ошибки. Тогда в результате прохождения возмущения 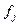по каналу, образованному с помощью УУ (параметры этого канала определяются коэффициентами полинома 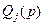), будет сформировано управляющее воздействие, которое полностью скомпенсирует влияние данного возмущения на объект управления.

Другими словами, в этом случае замкнутая система автоматического управления теоретически будет абсолютно инвариантной (см. § 5.6) к измеряемому возмущению 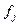. Практически же неизбежные погрешности приведут к отличным от нуля (в пределах точности настройки УУ) коэффициентам ошибки по данному возмущению, т.е. будет достигнута так называемая инвариантность с точностью до 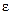. Воздействие, по отношению к которому система обладает такой инвариантностью, вызывает ошибки, не превышающие весьма малой величины 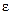, поэтому системы с инвариантностью до 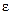очень ценны с практической точки зрения.

Если условие (8.36) не выполняется, т.е. 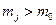, то по отношению к данному возмущению 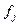указанной инвариантности достичь невозможно. Тогда коэффициенты 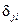числителя передаточной функции по этому возмущению наиболее целесообразно выбирать либо по условиям астатизма, либо путем минимизации интегральных оценок (см. пример 8.1).

В качестве примера синтеза систем управления минимально-фазовым объектом рассмотрим задачу синтеза абсолютно инвариантной системы к задающему воздействию и измеряемому возмущению без применения вырожденного (сингулярного) УУ.

Пример 8.2. Уравнение состояний объекта управления имеет вид (7.1) с матрицей и векторами:

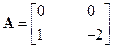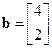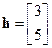, , . (8.37)

Уравнение выхода 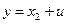, т.е. вектор 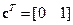. Синтезировать систему автоматического управления, ошибка которой 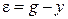в установившемся режиме будет абсолютно инвариантной по отношению к задающему воздействию g и к измеряемому возмущению f.

Решение. По формулам (5.17), (5.18) пр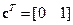и и 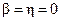находим для заданного объекта

, , .

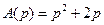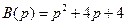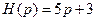Так как полином 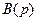удовлетворяет критерию Гурвица (см. § 4.3), то заданный объект управления (7.1), (8.37) является минимально-фазовым, причем 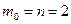, а 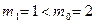. Поэтому из (8.36) следует, что поставленная задача имеет решение.

Переходя к расчету устройства управления, с помощью соотношений (8.28) и (8.30) найдем 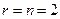, , 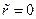т.е. можно положить 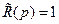. При этом, степень полинома 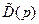в (8.25), равная 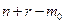, будет равна 2. Коэффициент 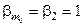, поэтому на основании равенства (8.24) имеем 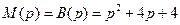. Исходя из условий устойчивости, примем 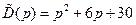. В данном случае 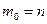, поэтому полином 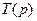и величины 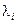найдем по формулам (8.31) и (8.32). Подставляя численные значения, получим , , , .

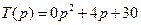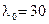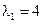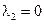Для обеспечения инвариантности замкнутой системы в соответствии формулами (5.41) и (5.42) примем 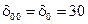, , 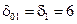, 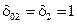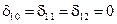. Затем по формулам (8.33) – (8.35) получим , , , , , .

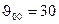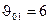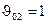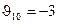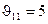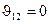Из равенства (8.26), с учетом найденных выражений для полиномов 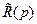, 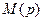и условия 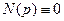, следует 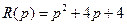. Подставляя численные значения величин 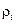, , 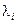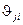в формулы (8.17), найдем коэффициенты, а с помощью равенств (8.1), (8.2) запишем уравнения искомого устройства управления в переменных состояния

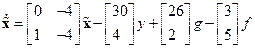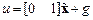, . (8.38)

Этим уравнениям соответствует структурная схема, приведенная на рис. 8.2. Для исследования свойств синтезированной системы объединим уравнения объекта и устройства управления, исключив управление 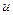. Это приводит к уравнениям:

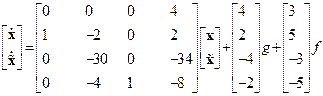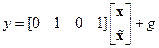, . (8.39)

Проверку инвариантности этой системы можно провести с помощью приведённых выше условий абсолютной инвариантности (5.51), (5.52) или же (5.50). Вычисляя, например, передаточные функци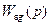и и 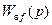системы (8.38), (8.39), найдем, что они тождественно равны нулю. Это соответствует условиям абсолютной инвариантности в форме (5.50).

Более полную оценку качества синтезированной системы можно получить на основе результатов её численного моделирования, приведенных на рис. 8.3. На этом рисунке показаны: штрих пунктирной линией график задающего воздействия 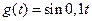, штриховой линией – график возмущения 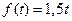, а сплошной линией – график отклонения 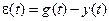при начальных условиях: x₁₀ = 1, x₂₀ = 2, z₁₀ = 3, z₂₀ = 4.

Как видно из графиков, в установившемся режиме отклонение системы равно нулю. Аналогичный вид имеет график отклонения системы и при других воздействиях. Это свидетельствует, что синтезированная система является абсолютно инвариантной к внешним воздействиям.

Анализ уравнений системы (8.38), (8.39) приводит к выводу, что переходные процессы в синтезированной системе возникают только при ненулевых начальных условиях по переменным состояния. Причем заканчиваются они, за время за время 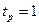с, что соответствует оценке (6.10), так как степень устойчивости η, фигурирующая в формуле (6.10), в данном случае определяется нулями полинома 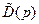и равна 3. Этот вывод подтверждается также графиком отклонения 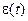, приведённым на рис. 8.3.

При нулевых начальных условиях по переменным состояния, т.е. при x₁₀ = x₂₀ = z₁₀ = z₂₀ = 0, и любом ограниченном возмущении 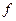график выходного сигнала системы (8.38), (8.39) при всех 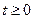полностью совпадает с кривой её задающего воздействия 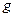. При ненулевых начальных условиях по переменным состояния выходной сигнал синтезированной системы совпадает с задающим воздействием только в установившемся режиме.

Следовательно, если параметры заданного объекта и устройства управления в точности равны указанным выше значениям, то в установившемся режиме на выходе объекта будет безошибочно воспроизводиться произвольное, ограниченное задающее воздействие g при любом ограниченном измеряемом возмущении f.

Конечно, на практике обеспечить идеальное соответствие реальных параметров расчетным значениям невозможно. Поэтому реальная система (модель которой описывается уравнениями (8.38), (8.39)) будет иметь не нулевую ошибку в установившемся режиме. Величина этой ошибки, как отмечалось выше, определяется погрешностями определения коэффициентов уравнений реального объекта и неточностью реализации уравнений устройства управления.