Определение управления по выходу и воздействиям

На практике часто применяются системы автоматического управления, в которых управление по отклонению комбинируется с управлением по воздействиям. Качество таких систем, как правило, значительно выше, чем систем с управлением только по отклонению. Однако обратная связь по выходу используется здесь не в полной мере, так как в основном служит для формирования отклонения.

Рассмотренные выше модальное и оптимальное управления реализуются чаще всего с помощью наблюдателей состояния. При наличии возмущений, приложенных к объекту, в уравнения наблюдателя должны входить эти возмущения наряду с управлением, и формально это приводит к зависимости управления от задающего воздействия и от возмущений. Однако связи по этим воздействиям также не варьируются с целью улучшения качества процесса управления, а предопределены заранее уравнениями наблюдателя. Поэтому получаемые таким способом управления оказываются управлениями только по состоянию. Их синтез сводится к выбору варьируемых обратных связей по состоянию x и по выходу y (фактически, по оценкам состояния 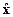и по выходу y).

В устройстве управления (7.25), реализующем управление по выходу и по воздействиям, варьируемыми предполагаются все вводимые в нём связи, т.е. по управлению u, по измеряемой величине y, по задающему воздействию g и по измеряемым возмущениям .

Рассмотрим структурные особенности систем с управлением по выходу и по воздействиям на примере системы управления объектом с одним управлением и одним выходом.

Функциональная схема такой системы приведена на рис. 8.1. Здесь предполагается, что объект управления (ОУ) задан либо уравнениями в переменных состояния (5.15), (5.16) или (7.1), (7.2), либо уравнением «вход-выход» (7.24). Устройство управления (УУ) представляет собой динамический блок, имеющий один выход и несколько входов, на которые подаются все доступные измерению воздействия и переменные. Это задающее воздействие g и измеряемое возмущение f, управление u и управляемая переменная y. Причем две последние связи берутся отрицательными.

Поэтому в соответствии с рис. 8.1 уравнения рассматриваемого УУ в переменных состояния можно записать так:

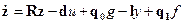, (8.1)

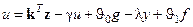. 8.2)

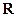Здесь – r-мерный вектор переменных состояния УУ; – матрица; 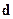, , 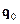, , 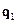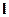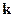– векторы соответствующей размерности; 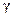, , , 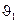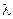– числовые коэффициенты.

В уравнениях (8.1), (8.2) размерность вектора z, а также все коэффициенты предполагаются варьируемыми, причем все они заранее неизвестны и должны быть определены в процессе синтеза системы управления, исходя из требований к ее качеству.

Известно, что уравнениям (8.1), (8.2) всегда можно поставить в соответствие некоторую электрическую схему, поэтому УУ, которое описывается уравнениями такого типа, всегда может быть физически реализовано.

Чтобы получить расчетные соотношения, позволяющие определить коэффициенты уравнений (8.1), (8.2), рассмотрим уравнения «вход-выход» замкнутой системы. Наиболее корректный путь получения этих уравнений состоит в объединении уравнений объекта (5.15), (5.16) и устройства управления (8.1), (8.2) с последующим исключением управления и всех переменных состояния. Однако этот путь является чрезвычайно громоздким. Гораздо проще искомое уравнение можно получить непосредственно из уравнений «вход-выход» объекта и устройства управления. Однако при этом, проводя преобразования уравнений, необходимо следить, чтобы порядок системы всегда был равен сумме порядков объекта и устройства управления.

В изображениях по Лапласу при нулевых начальных условиях уравнение вход-выход

УУ (8.1), (8.2) имеет вид

, (8.3)

где

, ,

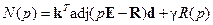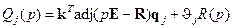, , (8.4)

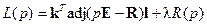Подставляя выражение для 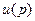, которое вытекает из уравнения (8.3), в уравнение «вход-выход» (7.24) объекта пр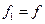и и 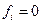, , 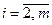придём к уравнению

, (8.5)

где обозначено

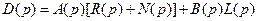, (8.6)

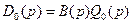, (8.7)

. (8.8)

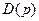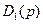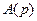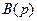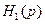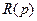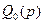В этих выражениях коэффициенты полиномов , и являются коэффициентами уравнения «вход-выход» (8.5) замкнутой системы, а коэффициенты полиномов , , и , , , , – коэффициентами уравнений вход-выход объекта (7.24) и управляющего устройства (8.3) соответственно. Следовательно, соотношения (8.6) – (8.8) устанавливают связь между параметрами замкнутой системы, объекта и устройства управления.

Коэффициенты полиномов 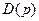, и 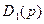одновременно являются и коэффициентами передаточных функций замкнутой системы. Действительно, из уравнения (8.5) следуют выражения

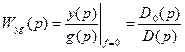, (8.9)

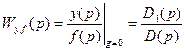. (8.10)

Таким образом, полином 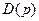является знаменателем, а полиномы и 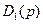– числителями передаточных функций замкнутой системы по задающему и возмущающему воздействиям.

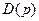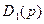Передаточные функции, как известно, достаточно полно определяют качество системы управления. Следовательно, исходя из требуемых свойств системы, можно указать желаемые значения коэффициентов полиномов , и . При заданных полиномах 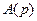, 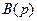и 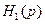это позволяет рассматривать соотношения (8.6) – (8.8) как систему полиномиальных уравнений относительно неизвестных полиномов или коэффициентов управляющего устройства, описываемого уравнением (8.3).

При таком (полиномиальном) подходе синтез систем автоматического управления сводится к следующим действиям:

а) выбору порядка замкнутой системы управления, исходя из условий разрешимости уравнений (8.6) – (8.8) и условий физической реализуемости модели УУ (8.3);

б) выбору желаемых значений коэффициентов передаточных функций замкнутой системы (8.9), (8.10), исходя из заданных требований к качеству процесса управления;

в) решению систем уравнений, определяющих коэффициенты искомого устройства управления.

Важнейшим преимуществом такого подхода к синтезу систем автоматического управления является то, что указанные задачи могут разрешаться достаточно независимо. Кроме того, системы уравнений, определяющие параметры устройства управления, являются алгебраическими и линейными. Это позволяет достаточно просто разрешить указанные системы, в том числе и в тех случаях, когда некоторые параметры замкнутой системы остаются неизвестными, варьируемыми. Их значения выбираются путём оптимизации тех или иных критериев качества замкнутой системы.

Соотношения (8.1) – (8.8) допускают большое число различных вариантов синтеза систем автоматического управления. В частности, приведённые выше решения задач синтеза инвариантных систем управления (§ 7.5) получены с применением именно управления по выходу и по воздействиями и этих соотношений. В данной главе рассматриваются решения на основе этого же подхода ряда других, часто встречающихся на практике задач.

Прежде чем переходить к их изложению, сделаем несколько замечаний. Основной особенностью данного подхода является возможность назначения всех коэффициентов (корней) знаменателей передаточных функций и частичная (в общем случае) возможность назначения коэффициентов числителей передаточных функций (8.9), (8.10). Поэтому возможности того или иного варианта синтеза, в конечном счете, определяются тем, какое число этих коэффициентов можно назначить, исходя из требований к качеству системы управления. 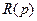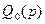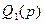Это, в свою очередь, определяется условиями разрешимости уравнений (8.6) – (8.8) относительно коэффициентов полиномов , , , и при заданных полиномах 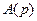, 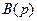и 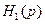и условиях физической реализуемости УУ (8.3).

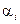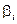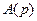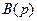Например, возможности одного из вариантов синтеза определяются приведённой ниже теоремой. Пусть , , – коэффициенты при полиномов , и 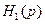из уравнения (7.24), причем 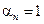; а 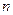, , 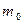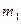– степени этих полиномов соответственно. Обозначим через – число такое, что

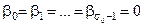, . (8.11)

По существу, – это число нулей полинома 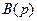, расположенных в точке р = 0.

Теорема 8.1. Пусть заданный объект (8.1), (8.2) n-го порядка является полным, выполнено (8.11), а порядок r устройства управления (8.1), (8.2) удовлетворяет неравенству

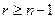. (8.12)

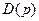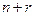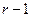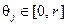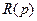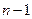Тогда при любом заданном полиноме степени , любом заданном полиноме степени и любых целых числах уравнения (8.6) – (8.8) разрешимы относительно неизвестных коэффициентов полиномов: степени , степени и степени 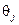, . При этом число назначаемых коэффициентов полиномов определяется выражением

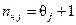или 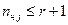, (8.13)

а число 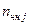не назначаемых коэффициентов 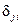– формулой

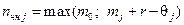. ■ (8.14)

В общем случае полиномы в уравнении УУ (8.3) определяются следующим образом. Будем считать, что коэффициенты полиномов 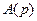, , 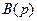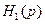заданы, полинома 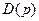назначены, исходя из требуемых свойств системы. При этом полиномы 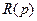, , , 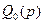и полином 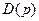имеют вид

, , ,

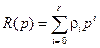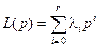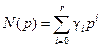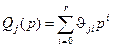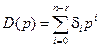, . (8.15)

Перемножая полиномы в левой части равенства (8.6) с учетом обозначений (8.15) и приравнивая коэффициенты при одинаковых степенях в левой и правой его частях, получим систему алгебраических уравнений вида

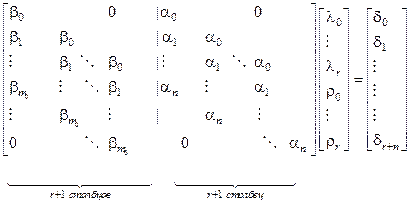, (8.16)

Степени полиномов 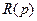и выбираются так, чтобы матрица этой системы была квадратной (как, например, при ). При этом если объект управления является полным, то её определитель не равен нулю, и алгебраическая система (8.16) имеет единственное решение, которое полностью определяет указанные в (8.15) коэффициенты полиномов и .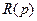

Аналогично путем перехода к матричной форме разрешаются уравнения (8.7) и (8.8) относительно коэффициентов полиномов 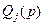, после выбора желаемых значений назначаемых коэффициентов 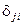, 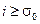полиномов , .

Как видно из соотношений (8.6), (8.8), полиномы 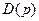и 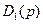зависят не отдельно от каждого полинома 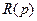и , а от их суммы. Поэтому коэффициенты одного из них (обычно ) выбираются с учетом конкретных требований к качеству системы (см. пример 7.3) или конструктивных соображений.

После того как все полиномы (8.15) найдены, коэффициенты уравнений УУ в форме (8.1), (8.2) наиболее целесообразно определять в соответствии с выражениями:

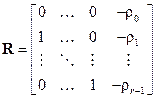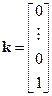, , (8.17)

, , , .

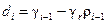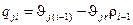Здесь 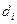, , 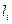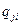– компоненты векторов 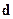, , 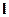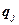соответственно.

Выражения (8.17) по смыслу являются «обратными» к соотношениям (8.4). Фактически это соотношения «обратного» перехода от уравнения «вход-выход» к соответствующим уравнениям в переменных состояния на основе канонической наблюдаемой формы.

Конечно, коэффициенты уравнений устройства управления (8.1), (8.2) могут вычисляться и другим путем. С точки зрения синтеза системы управления важно только, чтобы уравнение «вход-выход» полученного УУ имело найденные выше полиномы (8.15).

Перейдём к рассмотрению решения задач синтеза САУ различных типов на основе приведённых соотношений.

§ 8.2. Синтез систем управления с вырожденными передаточными функциями

Из теоремы 8.1 следует, что порядок замкнутой системы с управлением по выходу и

воздействиям не ниже 2n – 1, т.е. является довольно высоким. Так как выбор желаемых передаточных функций системы высокого порядка затруднителен, то целесообразно понизить степени знаменателей и числителей передаточных функций синтезируемой системы. Это можно сделать, выбрав порядок r устройства управления, согласно (8.12), а полиномы в уравнениях (8.6) – (8.8) взяв в виде

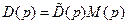, (8.18)

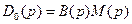, (8.19)

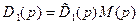. (8.20)

Здесь 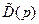– желаемый полином знаменателей передаточных функций системы n-го порядка; 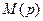– вспомогательный полином, удовлетворяющий условиям Гурвица; 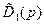– также вспомогательный полином.

Подставив выражения (8.18) – (8.20) в равенства (8.9), (8.10), получим:

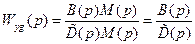, (8.21)

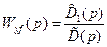. (8.22)

Таким образом, передаточные функции замкнутой системы в условиях равенств (8.18) – (8.20) являются вырожденными (из-за сокращения полинома 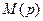) и соответствуют системе, порядок которой равен порядку объекта, так как степень полинома 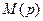можно взять равной .

Напомним, что этими же свойствами обладают и рассмотренные выше системы с на-

блюдателем Калмана (см. § 7.4). Полином 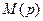в равенствах (8.18) – (8.21) эквивалентен характеристическому полиному наблюдателя 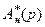из выражения (7.19). Поэтому его нули целесообразно выбирать несколько левее нулей полинома 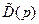. В свою очередь, последний эквивалентен, очевидно, полиному 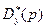из того же выражения (7.19).

Следовательно, если полиномы 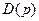и выбраны, согласно (8.18) – (8.20), то соотношения (8.6) – (8.8) определяют при 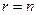САУ с наблюдателем Калмана. При этом коэффициенты числителей передаточных функций замкнутой системы, как отмечалось выше, выбирать по тем или иным условиям синтеза невозможно, так как имеющиеся в ней возможности назначения коэффициентов «расходуются» на обеспечение вырожденности её передаточных функций (8.21), (8.22).

Числитель передаточной функции (8.21) и здесь оказывается тем же, что и у передаточной функции по управлению u объекта (7.24). В то же время числители передаточных функций по возмущениям изменяются и заранее неизвестны.

Решение задачи синтеза при условиях (8.18) – (8.20) существует, если только заданный объект стабилизируемый. Для определения параметров устройства управления (8.1) – (8.2) необходимо выбрать величину r, полиномы 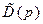и 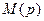, затем составить и решить систему (8.16), соответствующую равенству (8.6) с учетом (8.15), а также аналогичные системы, соответствующие равенствам (8.7) и (8.8). Затем воспользоваться формулами (8.17) для матрицы Rи векторов 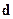, , 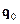, , 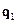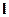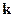из уравнений (8.1), (8.2) устройства управления. Тот факт, что числитель передаточной функции (8.21) известен заранее, можно использовать для выбора полинома 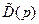с учётом того или иного требования к качеству системы. Покажем эти возможности.

Пример 8.1. Синтезировать систему, оптимальную в смысле минимума интегральной квадратичной оценки (6.2) переходной функции по задающему воздействию. Объект управления – механизм подачи электрода в сварочную головку, который описывается уравнения-

ми (5.15), (5.16) с числами 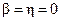, матрицей и векторами

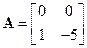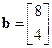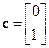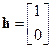, , , . (8.23)

Необходимо рассчитать параметры устройства управления, обеспечивающего равенство нулю коэффициента ошибки 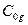по задающему воздействию и оптимальность САУ в указанном смысле. При этом возмущение f измерению недоступно.

Решение. Матрицы управляемости и наблюдаемости заданного объекта (8.23), по формулам (3.3) и (3.16) при B= b и 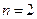, имеют вид

, .

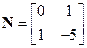Определители этих матриц не равны нулю, следовательно, объект полный, и задача синтеза имеет решение. Переходя в (5.15), (5.16) с учетом (8.23) к уравнению вход-выход (7.24) по (5.17), (5.18), получим

, , .

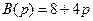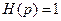Для обеспечения равенства 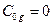, в соответствии с формулой (5.41), возьмем , т.е. . Неизвестный коэффициент будем считать варьируемым и выберем его из условия оптимальности. В силу равенства (8.21) изображение по Лапласу переходной функции замкнутой системы по задающему воздействию 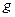в данном случае имеет вид

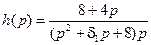Воспользовавшись формулами (6.6), (6.7) и формулами Мак-Ленна (см. § 5.7) при 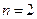, получим квадратичную интегральную оценку переходной функции синтезируемой системы в виде

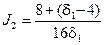Эта оценка имеет минимум при . Округляя без существенных потерь это значение до 5, получим желаемый полином 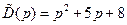. Его нули .

Степень полинома 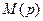(при равенстве в формуле (8.12)) . Примем его нуль равным –3 так, чтобы его реальная часть по модулю была больше 2,5. Тогда 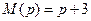. При этом по формуле (8.18) полином .

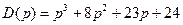Система (8.16), соответствующая уравнению (8.6), в данном случае имеет вид

Ее решение: , , , .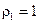

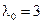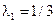Подставляя равенство (8.19) в уравнение (8.7), находим , т.е. 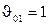. Далее по формулам (8.17) при 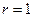, 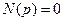и имеем , , 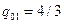, 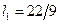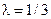. Поэтому в соответствии с равенствами (8.1), (8.2) уравнения устройства управления вданном случае имеют вид

, .

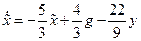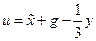Объединяя уравнения объекта (5.15), (5.16), (8.23) с этими уравнениями УУ в одну систему и исключая переменные состояния 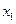, , 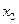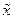и управление 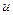, получим (после сокращения на множитель 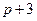) передаточную функцию замкнутой системы

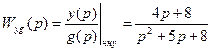Коэффициент 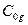этой системы, согласно (5.37), равен нулю. Нетрудно убедиться также, что характеристический полином синтезированной системы равен произведению 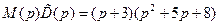, что характерно, как отмечалось выше, для систем с наблюдающими устройствами. ■