Второе уравнение Максвелла.
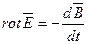 (6.1) Физический смысл этого уравнения состоит в том, что всякое изменение магнитного поля во времени (
(6.1) Физический смысл этого уравнения состоит в том, что всякое изменение магнитного поля во времени ( 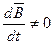 ) в какой либо точке поля возбуждает вихрь или ротор электрического поля (
) в какой либо точке поля возбуждает вихрь или ротор электрического поля ( 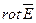 ) в той же точке поля, т.е. вызывает вихревое электрическое поле.
) в той же точке поля, т.е. вызывает вихревое электрическое поле.
Второе уравнение Максвелла представляет собой дифференциальную форму закона электрической индукции.
Чтобы убедиться в этом, мысленно возьмем некоторый замкнуты контур, расположенный в переменном электрическом поле. Переменный магнитный поток, пронизывающий контур, наведет в нем ЭДС.
 , где Ф - магнитный поток (поток магнитной индукции). Если магнитное поле однородное, то Ф через плоскую поверхность с площадью S, равен
, где Ф - магнитный поток (поток магнитной индукции). Если магнитное поле однородное, то Ф через плоскую поверхность с площадью S, равен  ,
,
но 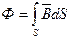 , поэтому
, поэтому 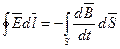 , причем площадка
, причем площадка 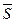 опирается на контур
опирается на контур 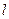 .
.
На основании теории Стокса  , поэтому
, поэтому 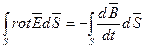 .
.
Это равенство должно выполняться при любых площадях S, то возможно только в том случае, когда равны подынтегральные функции обоих интегралов, следовательно 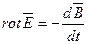 .
.
Знак «минус» в данной форме, как и в формуле  , объясняется тем, что в основу положено правило правого винта (правилом буравчика). Если завинчивать правый винт так, что положительное направление вектора магнитной индукции
, объясняется тем, что в основу положено правило правого винта (правилом буравчика). Если завинчивать правый винт так, что положительное направление вектора магнитной индукции 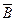 в некоторой точке пространства при возрастании индукции в этой точке совпадает с направлением острия винта, то положительное направление для вектора напряженности электрического поля
в некоторой точке пространства при возрастании индукции в этой точке совпадает с направлением острия винта, то положительное направление для вектора напряженности электрического поля 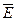 при составлении циркуляции вектора
при составлении циркуляции вектора 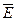 бесконечно малого контура, окружающего эту точку и лежащего в плоскости, перпендикулярно вектору
бесконечно малого контура, окружающего эту точку и лежащего в плоскости, перпендикулярно вектору 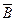 , совпадает с направлением вращения головки винта. Знак «минус» в правой части уравнения (6.1) поставлен для того, чтобы привести в соответствие действительное направление для
, совпадает с направлением вращения головки винта. Знак «минус» в правой части уравнения (6.1) поставлен для того, чтобы привести в соответствие действительное направление для 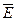 при оговоренных ранее условиях с направлением, принятым для
при оговоренных ранее условиях с направлением, принятым для 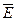 за положительное.
за положительное.
Как в первом, так и во втором уравнение Максвелла участвуют частные (не полные)
производные во времени. Это объясняется тем, что уравнения Максвелла записаны для таких тел и контуров, которые неподвижны к выбранной системе координат.
В переменном электромагнитном поле кроме силовых линий электрического поля, «начинающихся» и «оканчивающихся» на электрических зарядах (как в электростатическом поле) могу быть и замкнутые на себе силовые линии электростатического поля, охватывающие замкнутые на себя силовые линии магнитного поля.
7.Уравнение Максвелла в комплексной форме записи.
Уравнение 2.1 и 6.1 записаны для мгновенных значений Н и Е. Если Н и Е изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать эти уравнения в комплексной форме. Т.к.  и
и 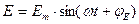 , в соответствии с формулой Эйлером :
, в соответствии с формулой Эйлером : 
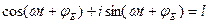
можно записать 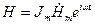 , где
, где 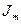 - мнимая часть или условно,
- мнимая часть или условно, 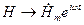 , где комплексная амплитуда
, где комплексная амплитуда 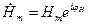 . Аналогично
. Аналогично 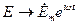 (
( 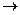 значок соответствия).
значок соответствия).
Т.к. напряженности Е и Н, кроме того, что они меняются во времени по синусоидальному закону являются функциями векторными, т.е. определенным образом ориентированными в пространстве векторам, то над ними ставят черточку и точку: 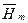 и
и 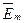 .
.
Черточка означает, что речь идет о векторе в пространстве, точка - о том, что проекция этого вектора на любую из координатных осей, во времени изменяется синусоидально.
Тогда 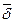 можно заменить на
можно заменить на 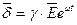 , где
, где 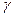 - удельная проводимость, характеризующая свойство среды проводить ток,
- удельная проводимость, характеризующая свойство среды проводить ток, 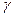 зависит от физических свойств проводящего материала и температуры. Измеряется в
зависит от физических свойств проводящего материала и температуры. Измеряется в 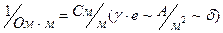
Так как 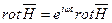 (
(  как постоянную величину можно вынести за знак ротора). После преобразования первое уравнение Максвелла в комплексной форме будет иметь вид:
как постоянную величину можно вынести за знак ротора). После преобразования первое уравнение Максвелла в комплексной форме будет иметь вид: 
Соответственно второе уравнение Максвелла в комплексной форме будет иметь вид: 
8.Построить линии уровня плоских скалярных полей: 1) 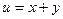 2)
2)  3)
3) 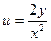 , соответствующее значениям u=1,2,3,4,5.
, соответствующее значениям u=1,2,3,4,5.
Скалярным полем называется плоская или пространственная область с каждой точкой М с которой связанно определенное значение некоторой скалярной физической величины U=U(М).
Задание скалярной величины и равносильно заданию скалярной (числовой) функции U(M).Функция U(M), определяющая плоское скалярное поле, как функция точки М(х,у), зависит от двух переменных U=u(х,у).
Линией уровня плоского скалярного поля называют совокупность точек плоскости, в которых функция этого поля имеет одинаковые значения.
Линия уровня, во всех точках которых функция поля U(х,у) имеет одно и тоже значении С, определяется уравнением U(х,у)=С; различным постоянным значениям 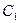 ,
, 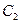 ,
, 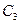 …функции поля соответствуют различные линии уровня: U(х,у) =
…функции поля соответствуют различные линии уровня: U(х,у) = 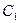 , U(х,у) =
, U(х,у) = 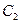 , U(х,у) =
, U(х,у) = 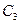
Решение:
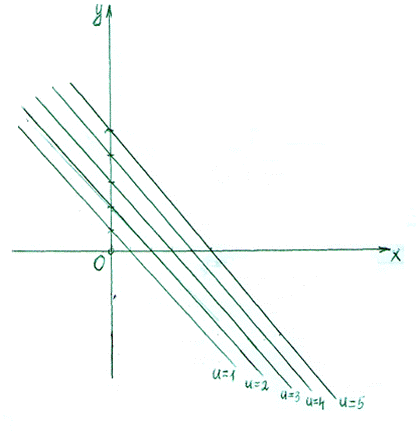
1)Пологая U=1,2,3,4,5,получим уравнения соответствующих линий уровня: х+у=1, х+у=2,
х+у=3, х+у=4, х+у=5. Построив эти линии в прямоугольной системе координат ХОУ, получим прямые параллельные биссектрисе 2-го и 4-го координатных углов, которые и являются геометрической интерпретацией линий уровня скалярного поля.
2)Написав уравнения линий уровня: 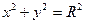 ; (
; ( 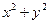 =1;
=1; 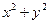 =2;
=2; 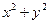 =3;
=3; 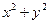 =4;
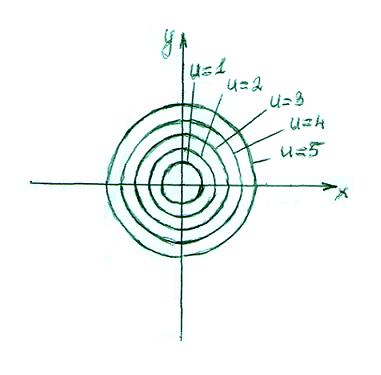
=4; 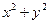 =5) построив их в плоскости ХОУ получим окружности с радиусом R с центром в начале координат(R=1;1,4;1,7;2;2,2)
=5) построив их в плоскости ХОУ получим окружности с радиусом R с центром в начале координат(R=1;1,4;1,7;2;2,2)
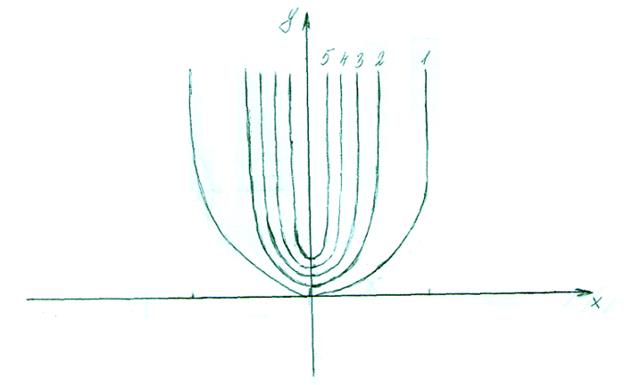
3) Линии уровня: 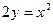 ,
,  ,
,  ,
, 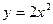 ,
, 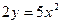 представляют собой параболы симметричные оси ОУ с общей вершиной в начале координат.
представляют собой параболы симметричные оси ОУ с общей вершиной в начале координат.
9.Найти производную функцию 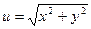 в точке М(3,4):
в точке М(3,4):
1)по сравнению биссектрисы 1-го координатного угла;
2)по направлению радиус-вектора точки М;
3)по направлению вектора 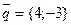
Производной функции U(M) по направлению 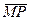 называют предел отношения разности
называют предел отношения разности 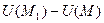 к величине направленного отрезка
к величине направленного отрезка 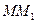 , когда точка
, когда точка  стремится к точке М, оставаясь на прямой МР.
стремится к точке М, оставаясь на прямой МР.
Производная функция U направлению 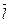 обозначается
обозначается  или
или 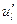 :
:
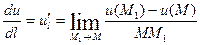
И вычисляется по формуле: 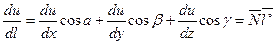 , где
, где
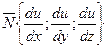 - нормальный вектор к поверхности уровня,
- нормальный вектор к поверхности уровня,
 - единичный вектор направления
- единичный вектор направления 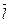
Производная  определяет величину скорости изменения функции U(M)при перемещении М по направлению
определяет величину скорости изменения функции U(M)при перемещении М по направлению 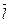 .
.
В каждой точке, где функция дифференцируемая, она имеет производную по любому направлению.
Производные функции U(x,y,z) по положительным направлениям осей координат 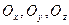 равны ее частным производным:
равны ее частным производным: 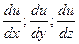
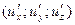 . Производные по прямо противоположным направлениям отличаются только по признаку.
. Производные по прямо противоположным направлениям отличаются только по признаку.
Производная функция U(х,у) по направлению линии уровня ( касательному к линии уровня) и производная функции U(x,y,z) по направлению любой линии, лежащей на поверхности уровня (по левому направлению, касательному к поверхностью уровня), равны нулю.
Решение:
Находим частные производственные функции U и вычисляем их значение в точке М.


Подставляя в формулу 
Находим далее косинусы углов  и
и  , образованных заданным направлением дифференцирования с осями координат, и производную функции U по заданному направлению:
, образованных заданным направлением дифференцирования с осями координат, и производную функции U по заданному направлению:
1)Для биссектрисы 1-го координатного угла: 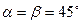 ,
, 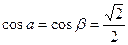 ,
, 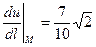 ;
;
2)Для радиус-вектора точки М: 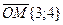 ,
,  ,
, 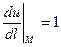 ;
;
3)Для вектора 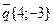 ,
, 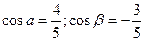 ,
,  .
.
10. По справочным данным: для вакуума 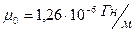 ,
, 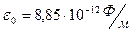 ; для воздуха
; для воздуха  ,
,  .
.
Определить скорость света в вакууме и скорость света в воздухе.
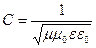 (
( 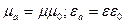 )
)
11. Составьте сравнительную таблицу единиц измерения основных электрических и магнитных величин. (Выразите их только через 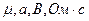 )
)
| Электрические величины | Магнитные величины |
Количество электричества (q)
Кл (Кулон) ~ 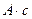 Напряжение, Э.д.с (U) В (Вольт)
Напряженность электрического поля (Е) В/м
Емкость (С) Ф (Фарада) ~ c/Ом
Абсолютная диэлектрическая проницаемость (
Напряжение, Э.д.с (U) В (Вольт)
Напряженность электрического поля (Е) В/м
Емкость (С) Ф (Фарада) ~ c/Ом
Абсолютная диэлектрическая проницаемость ( 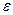 ) Ф/м ~ ) Ф/м ~ 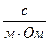
| Магнитный поток (Ф)
Вб (Вебер) ~ 
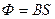 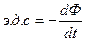 Магнитная индукция (В)
1Тл (Тесла) ~
Магнитная индукция (В)
1Тл (Тесла) ~ 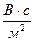 Напряженность магнитного поля (Н)
1А/м
Индуктивность Гн (Генри)
Напряженность магнитного поля (Н)
1А/м
Индуктивность Гн (Генри)  Абсолютная магнитная проницаемость (
Абсолютная магнитная проницаемость (  ) Гн/м ~ ) Гн/м ~ 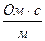
|
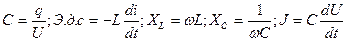
12. Найти поток векторного поля 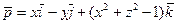 через поверхность эллипсоида
через поверхность эллипсоида 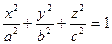 изнутри этой поверхности.
изнутри этой поверхности.
Векторным полем называется плоская или пространственная область, с каждой точкой М которой связано определенное значение некоторой физической величины 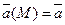 .
.
Если векторное поле отнесено к прямоугольной системе координат ОXYZ, то вектор будет векторной функцией, а его  проекции на оси координат будут скалярными функциями от переменных x,y,z:
проекции на оси координат будут скалярными функциями от переменных x,y,z:
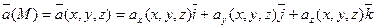
Поэтому задание поля векторной величины равносильно заданию трех скалярных (числовых) функций 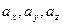 .
.
Потоком векторного поля, образованного вектором 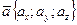 через поверхность называется поверхностный интеграл (скаляр)
через поверхность называется поверхностный интеграл (скаляр)
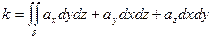 (1)
(1)
Если вектор 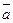 определяет поле скоростей текущей жидкости, то интеграл k выражает количество жидкости, протекающей через поверхность
определяет поле скоростей текущей жидкости, то интеграл k выражает количество жидкости, протекающей через поверхность 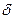 за единицу времени. При этом если
за единицу времени. При этом если 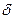 –замкнутая поверхность, ограничивающая область Q и если интеграл (1) берется по внешней стороне
–замкнутая поверхность, ограничивающая область Q и если интеграл (1) берется по внешней стороне 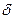 , то величина k называется потоком вектора
, то величина k называется потоком вектора 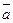 изнутри поверхности; она дает разность между количеством жидкости, вытекающей из области Q и втекающей в эту область за единицу времени (предполагается, что жидкость может свободно протекать через поверхность
изнутри поверхности; она дает разность между количеством жидкости, вытекающей из области Q и втекающей в эту область за единицу времени (предполагается, что жидкость может свободно протекать через поверхность 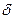 )
)
При k>0 из области Q вытекает жидкость больше, чем в нее втекает, что указывает на наличие в этой области источников, питающих поток жидкости. При k<0 из области вытекает жидкости меньше, чем втекает, что означает наличие в этой области стоков, где жидкость удаляется из потока. При k=0 из области вытекает жидкости столько же, сколько и втекает.
Решение Согласно (формуле 1)

Расчленяем этот поверхностный интеграл на три слагаемых интеграла и, пользуясь данным уравнением эллипсоида 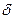 , сводим их вычисления к вычислению двойных интегралов.
, сводим их вычисления к вычислению двойных интегралов.
1) 
где  и
и 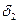 – части данного эллипсоида, расположенные по разные стороны от плоскостей yoz
– части данного эллипсоида, расположенные по разные стороны от плоскостей yoz
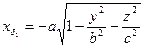 и
и 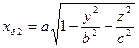
Преобразуя эти поверхностные интегралы в двойные, получим:
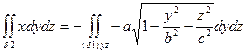
т.к. поверхность  обращена в сторону отрицательного направления оси ox
обращена в сторону отрицательного направления оси ox
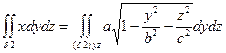
т.к. поверхность  обращена в сторону положительного направления ox.
обращена в сторону положительного направления ox.
Проекции  и
и 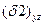 поверхностей
поверхностей  и
и  на плоскость yoz представляет один и тот же эллипс.
на плоскость yoz представляет один и тот же эллипс.
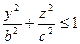
Поэтому:
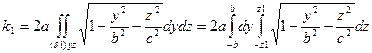
Где 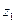 – положительное значение z из уравнения эллипса
– положительное значение z из уравнения эллипса
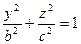
вычисляя двукратный интеграл, найдем
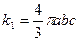
2) 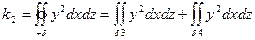
где 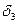 и
и 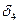 – части поверхности, расположенные по разные стороны от плоскости xoz, уравнения которых:
– части поверхности, расположенные по разные стороны от плоскости xoz, уравнения которых:
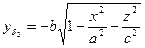 и
и 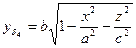
Преобразуя поверхностные интегралы в двойные, получим
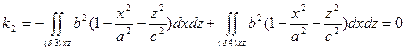
т.к. проекции 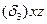 и
и  поверхностей на плоскость xoz одинаковы.
поверхностей на плоскость xoz одинаковы.
3) По аналогичной причине вследствие четности подынтегральной функции поверхностного интеграла 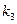 и симметричности поверхности
и симметричности поверхности 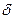 относительно плоскости xoy
относительно плоскости xoy
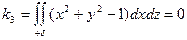
окончательно

13 Найти дивергенцию векторного поля:
1) 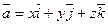 ; 2)
; 2) 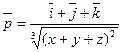 ; 3)
; 3) 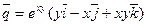 ;
;
Дивергенцией векторного поля, определяемого вектором, называют скаляр
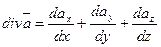 (2)
(2)
Если 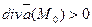 , то точку Мо называют источником, а если
, то точку Мо называют источником, а если 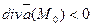 , то Мо называют стоком, ибо в первом случае в любой бесконечно малой области, окружающей точку Мо, жидкость возникает, а во втором случае она исчезает.
, то Мо называют стоком, ибо в первом случае в любой бесконечно малой области, окружающей точку Мо, жидкость возникает, а во втором случае она исчезает.
Абсолютная величина 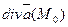 характеризует мощность источника или стока.
характеризует мощность источника или стока.
Векторное поле, во всех точках которого дивергенция равна нулю, называют соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
Согласно формуле Остроградского-Гаусса поток и дивергенция векторного поля связаны между собой равенством
 (3)
(3)
Которое имеет следующий смысл: поток векторного поля В через замкнутую поверхность 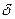 равен тройному интегралу по области , ограниченной этой поверхностью, от дивергенцией поля.
равен тройному интегралу по области , ограниченной этой поверхностью, от дивергенцией поля.
Решение. Применяя формулу (2):
1) 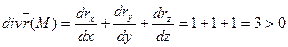
Физический смысл: каждая точка поля радиус-вектора 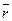 является источником постоянной мощности
является источником постоянной мощности
2) 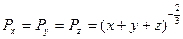

Физический смысл: точка поля М вектора 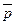 в зависимости от ее координат может быть или источником, или стоком. Например, точка
в зависимости от ее координат может быть или источником, или стоком. Например, точка 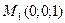 в которой
в которой
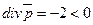
является стоком; точка 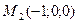 в которой
в которой

является источником.
3) 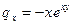
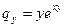
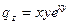
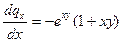 ;
; 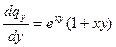 ;
; 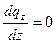
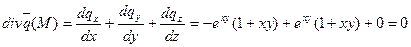
Физический смысл: В поле вектора  нет ни источников, ни стоков. Поток этого соленоидного поля через любую замкнутую поверхность равен нулю.
нет ни источников, ни стоков. Поток этого соленоидного поля через любую замкнутую поверхность равен нулю.
14. Используя формулу Остроградского-Гаусса решить задачу 12, т.е. найти поток векторного 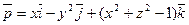 через поверхность эллипсоида
через поверхность эллипсоида 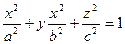 изнутри этой поверхности.
изнутри этой поверхности.
Решение. Найдем
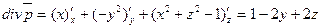 и подставляя в формулу (3) найдем
и подставляя в формулу (3) найдем
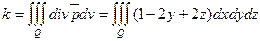
где Q– эллипсоид 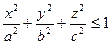
Полученный тройной интеграл расчленяем:
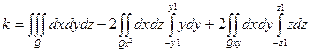
Где 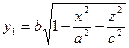 и
и 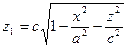
Первый интеграл равен объему области Q, т.е. объему эллипсоида 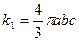
Второй и третий интегралы равны, т.к. равны нулю их внутренние простые интегралы от нечетной функции.
Следовательно, как и в решении задачи 12 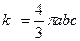 , Но решение значительно проще.
, Но решение значительно проще.
15. Найти дивергенцию векторного поля 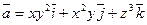 в точке А(1;-1;3)
в точке А(1;-1;3)
Решение: 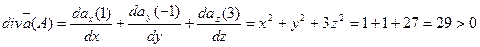
в точке А исток
16. Проверить, что векторное поле  является соленоидным.
является соленоидным.
Решение:
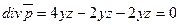
Во всех точках данного векторного поля 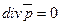 . Следовательно, векторное поле является соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
. Следовательно, векторное поле является соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
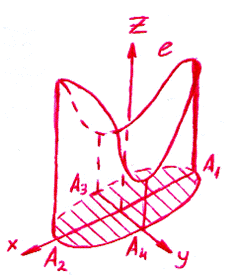
17. Вычислить циркуляцию поля вектора 1)  вдоль окружности
вдоль окружности  2)
2) 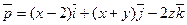 вдоль периметра треугольника с вершинами А(1;0;0) В(0;1;0) С(0;0;1); 3)
вдоль периметра треугольника с вершинами А(1;0;0) В(0;1;0) С(0;0;1); 3) 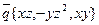 вдоль замкнутой линии (l):
вдоль замкнутой линии (l): 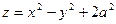 ,
, 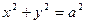 (см. рис) и вихревой вектор этого поля в точке А(
(см. рис) и вихревой вектор этого поля в точке А( 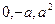 )
)
Линейным интегралом вектора 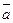 вдоль линии l называют криволинейный интеграл
вдоль линии l называют криволинейный интеграл 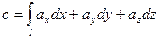 (1)
(1)
В силовом поле он выражает работу сил поля при перемещении точки вдоль линии l.
В случае замкнутой кривой этот интеграл называется циркуляцией поля вектора по контуру l.
Вихрем (или ротором) векторного поля, определяемого вектором 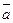 , называют вектор
, называют вектор
 (2)
(2)
Доказать!
Если через точку М поля 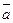 провести плоскость Р, определяемую единичным нормальным вектором
провести плоскость Р, определяемую единичным нормальным вектором 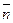 , то скалярное произведение
, то скалярное произведение 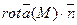 характеризует вращательную способность этого поля в точке М. Она зависит как от координат точки М, так и от направления плоскости Р и достигает наибольшей величины , равной
характеризует вращательную способность этого поля в точке М. Она зависит как от координат точки М, так и от направления плоскости Р и достигает наибольшей величины , равной  когда плоскость Р перпендикулярна
когда плоскость Р перпендикулярна  .
.
Векторное поле, во всех точках которого вихревой вектор равен нулю, называют потенциальным(или безвихревым). В потенциальном поле линейный интеграл, т.е. работа не зависит от формы линии, соединяющей какие-либо две его точки, а циркуляция всегда равна нулю.
Векторное поле, являющееся одновременно и соленоидальным и потенциальным, называют гармоническим.
Решение Применяя формулу (1), получим:
1) 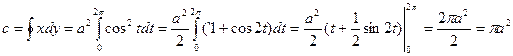
Если выбрать другое направление обхода данного контура, то результат будет иметь противоположный знак
2) 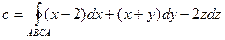
Периметр АВСА треугольника состоит из трёх отрезков, которые лежат на прямых, имеющих различные уравнения. Поэтому криволинейный интеграл по контуру АВСА вычисляем как сумму интегралов по отрезкам АВ, ВС и СА.
Составив уравнения прямой АВ: X+Y=1, Z=0 и исходя из этих уравнений преобразуем криволинейный интеграл по отрезку АВ в обыкновенный интеграл с переменной x.
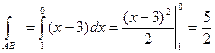
Для отрезка ВС: y+z=1; x=0;

Для отрезка СА; x+z=1, y=o;
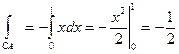
Следовательно 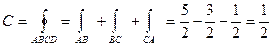
3) 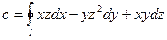
Для вычисления этого интеграла преобразуем данные уравнения кривой l в параметрические: полагая 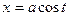 , получим из уравнения
, получим из уравнения 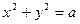 ,
, 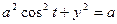 ,
, 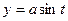
Соответственно из уравнения 
Пользуясь этими уравнениями, преобразуем криволинейный интеграл с в обыкновенный интеграл с переменной t, затем вычисляем его:
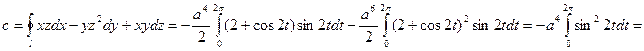
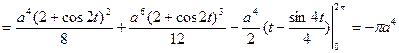
Вихревой вектор (rot) данного поля в любой точке М(x,y,z) находим по формуле (2)
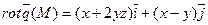
В данной точке А( 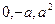 )
)
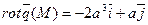
18. С какой наибольшей скоростью может возрастать функция  при переходе точки
при переходе точки  через точку
через точку 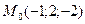 ? В каком направлении должна двигаться точка М при переходе через точку
? В каком направлении должна двигаться точка М при переходе через точку 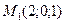 , чтобы функция убывала с наибольшей скоростью?
, чтобы функция убывала с наибольшей скоростью?
Наибольшая по величине скорость (возрастания или убывания) функции U(M) при переходе точки M через точку P численно равна модулю градиента функции в точке P. При этом функция будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка M, переходя через точку P, двигаться по направлению градиента функции в точке P или по прямо противоположному направлению.
В соответствии с данными положениями, находим частные производные U и по формуле 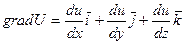 ее градиент в любой точке.
ее градиент в любой точке.
Градиентом функции (поля) U(M) называют вектор 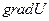 , который в каждой точке М совпадает с направлением нормали к поверхности (линии) уровня, проходящей через эту точку. Из всех производных функции U(M), взятых по различным направлениям, наибольшее значение всегда имеет производная по направлению градиента функции
, который в каждой точке М совпадает с направлением нормали к поверхности (линии) уровня, проходящей через эту точку. Из всех производных функции U(M), взятых по различным направлениям, наибольшее значение всегда имеет производная по направлению градиента функции
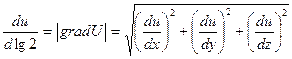
Градиент есть вектор скорости наибыстрейшего возрастания функции.

Далее находим:  ; его модуль численно равный искомой наибольшей скорости возрастания функции U(M) при переходе M через
; его модуль численно равный искомой наибольшей скорости возрастания функции U(M) при переходе M через  , будет:
, будет:
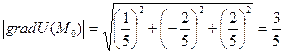
Далее: в каком направлении должна двигаться точка 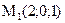 , чтобы функция U(M) убывала с наибольшей скоростью?
, чтобы функция U(M) убывала с наибольшей скоростью?
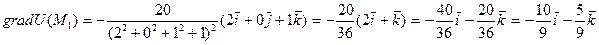
Чтобы функция U(M) убывала с наибольшей скоростью, при переходе через точку 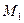 точка M должна двигаться в направлении вектора
точка M должна двигаться в направлении вектора

19. Найти производную функции 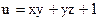 по направлению вектора
по направлению вектора 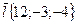 в любой точке и в точках
в любой точке и в точках 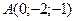 и
и  .
.
Найдем частные производные функции u и направляющие косинусы вектора 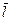 :
:
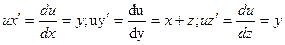 ;
;

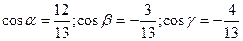
Подставляя в формулу:
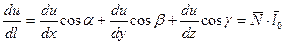
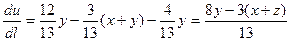
Подставляя координаты точек А и В получим:

20.Найти точки, в которых функция 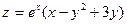 стационарна (т.е. точки, в которых производная по любому направлению равна нулю).
стационарна (т.е. точки, в которых производная по любому направлению равна нулю).
Чтобы в некоторой точке P производная функции по любому направлению была равна нулю, необходимо и достаточно, чтобы в этой точке все частные производные первого порядка функции одновременно обращались в нули. Согласно формуле:
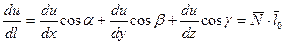 , где
, где 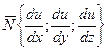 - нормальный вектор к поверхности уровня,
- нормальный вектор к поверхности уровня,  - единичный вектор направления
- единичный вектор направления 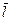 .
.
Поэтому, найдя частные производные:
 ,
, 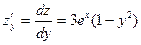 и решая систему уравнений:
и решая систему уравнений:
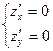 или
или 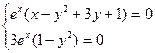 получим две точки: (-3;1) и (1;-1), функция
получим две точки: (-3;1) и (1;-1), функция 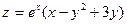 стационарна.
стационарна.
21. Найти вихревой вектор (rot) в любой точке векторного поля: 1) 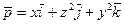 ; 2)
; 2) 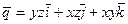 .
.
См. формулу 2 вопрос 17. Ответ: 1) 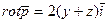 ; 2)
; 2) 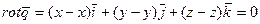 ;
;  - потенциальное поле (безвихревое).
- потенциальное поле (безвихревое).
22. Проверить, что векторное поле вектора 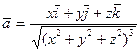 является гармоническим.
является гармоническим.
См. вопрос 17.
23. Найти линии уровня скалярного поля  соответствующие значениям z=-2,-1,0,1,2. См. вопрос 8. Найти градиент этого поля в точках A(1;-1) и B(-2;-2).
соответствующие значениям z=-2,-1,0,1,2. См. вопрос 8. Найти градиент этого поля в точках A(1;-1) и B(-2;-2).
Ответ: 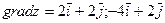
24. Теорема Умова-Пойнтинга.
Кроме уравнений Максвелла, большое значение в теории Электромагнитного поля имеет теорема Умова-Пойнтинга, которая описывает энергетические соотношения в поле.
Н.А. Умов с 1893 по 1911г. являлся профессором московского университета. В 1874г. защитил докторскую диссертацию «О движении Энергии в упругих средах», где рассмотрел вопрос о потоке энергии в упругих средах и о плотности потока энергии. Применительно к электромагнитному полю понятие о потоке энергии было развито Пойнтингом в 1885г.
Энергия электрического поля в единице объема равна 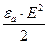 , соответственно энергия магнитного поля в единице объема
, соответственно энергия магнитного поля в единице объема 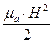 . Энергия в объеме
. Энергия в объеме  равна
равна  .
.
Можно показать, что 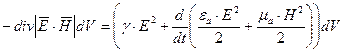 , где
, где 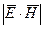 - векторное произведение
- векторное произведение 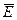 на
на 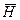 , для сокращения записи примем
, для сокращения записи примем  ;
;  - это вектор, называемый вектором Пойнтинга; размерность его равна произведению размерностей E и H, т.е.
- это вектор, называемый вектором Пойнтинга; размерность его равна произведению размерностей E и H, т.е.  .
.
Таким образом, вектор Пойнтинга имеет размерность мощности, отнесенной к единице поверхности и направление его совпадает с направлением движения острия правого винта, если головку последнего вращать по кротчайшему направлению от 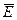 к
к 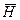 . Следовательно:
. Следовательно:
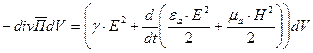 (1), где
(1), где 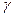 - удельная проводимость
- удельная проводимость 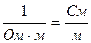 ;
;  - энергия, выделяющаяся в виде теплоты в единице объема в единицу времени;
- энергия, выделяющаяся в виде теплоты в единице объема в единицу времени; 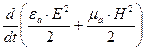 - скорость изменения запаса электромагнитной энергии в единице объема, в свою очередь скорость изменения электромагнитной энергии есть мощность.
- скорость изменения запаса электромагнитной энергии в единице объема, в свою очередь скорость изменения электромагнитной энергии есть мощность.
Рассмотрим (1) на некоторый объем конечных размеров. С этой целью проинтегрируем (1) по объему V:
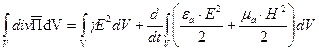 (2)
(2)
Можно показать, что:
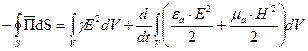 (3)
(3)
Формула (3) представляет собой теорему Умова-Пойнтинга для мгновенных значений. 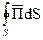 представляет собой поток вектора Пойнтинга сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.
представляет собой поток вектора Пойнтинга сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.
Т.к.  есть скорость изменения электромагнитной энергии, т.е. мощность, следовательно поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем V, равен мощности, выделяющейся на приращение энергии электромагнитного поля.
есть скорость изменения электромагнитной энергии, т.е. мощность, следовательно поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем V, равен мощности, выделяющейся на приращение энергии электромагнитного поля.
Теорему Умова-Пойнтинга следует трактовать как уравнение энергетического баланса.
Левая часть уравнения (3) есть мощность или энергия в единицу времени, доставляемая в виде потока вектора Пойнтинга внутрь некоторого объема; правая часть есть энергия, расходуемая в единицу времени внутри объема V.
Уравнение (3) было получено при условии, что среда внутри объема V однородна и изотропна- одинаковость (изотропия гр. tropos- поворот, направление) физ. свойств тела (среды) по всем направлениям. При обычных условиях газы, жидкости и аморфные тела изотропны, - а так же в предположении, что отсутствует отраженная волна и внутри объема нет источников электродвижущей силы. Если поле не изменяется во времени, то 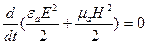 и
и 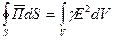
Следует также учесть, что уравнение (3) учитывает возможность прохождения потока вектора  транзитом через объем V.
транзитом через объем V.
25. Показать справедливость утверждения, что электромагнитная энергия от места ее генерирования передается к месту ее потребления по диэлектрику (провода же в линиях передачи выполняют двоякую роль: они являются каналами, по которым проходит ток и организаторами структуры поля в диэлектрике).
Пусть энергия постоянного тока передается по коаксиальному кабелю (см. рисунок). Радиус жилы:  , внутренний радиус оболочки:
, внутренний радиус оболочки: 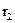 .
.
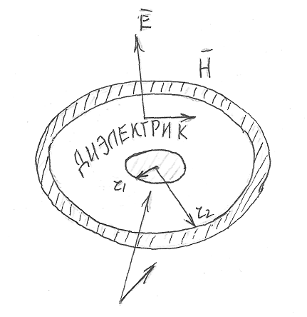
Примем проводимость материала жилы и оболочки настолько большой, что напряженности поля 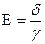 в жиле и оболочке стремятся к нулю. Пространство между жилой и оболочкой заполнено диэлектриком.
в жиле и оболочке стремятся к нулю. Пространство между жилой и оболочкой заполнено диэлектриком.
Убедимся, что энергия, передаваемая в единицу времени, равная 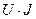 , действительно канализируется по диэлектрику.
, действительно канализируется по диэлектрику.
С этой целью подсчитаем поток вектора Пойнтинга через поперечное сечение диэлектрика, в рассматриваемом примере представляющее собой кольцо с внутренним радиусом 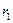 и наружным
и наружным 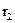 . Напряженность магнитного поля в диэлектрике по закону полного тока:
. Напряженность магнитного поля в диэлектрике по закону полного тока: 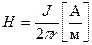 . Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики:
. Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики: 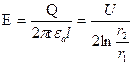 ,
,
где Q- полный заряд жилы на длине l; U- напряжение между жилой и оболочкой.
Следовательно, в некоторой точке диэлектрика, расположенной на расстоянии r от оси(  )
)
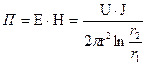 (
( 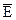 и
и 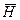 взаимно перпендикулярны).
взаимно перпендикулярны).
Поток вектора Пойнтинга через кольцо с радиусами 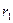 и
и 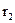 :
:
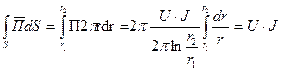
Таким образом, вся поступающая к приемнику энергия передается по диэлектрику. По жиле и оболочке энергия к приемнику не передается. Более того, если учесть, что 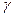 конечна и напряженность электрического поля в жиле и оболочке направлена по току и неравна нулю, то не трудно убедиться в наличии потока вектора Пойнтинга через боковую поверхность провода внутрь провода, т.е. провода сами потребляют энергию на покрытие тепловых потерь.
конечна и напряженность электрического поля в жиле и оболочке направлена по току и неравна нулю, то не трудно убедиться в наличии потока вектора Пойнтинга через боковую поверхность провода внутрь провода, т.е. провода сами потребляют энергию на покрытие тепловых потерь.
26. Определить  , составляемого напряженность электрического поля с нормалью к поверхности жилы в точке, принадлежащей поверхности жилы коаксиального кабеля, а также подсчитать величину поток вектора Пойнтинга через боковую поверхность жилы на длине в 1м. и сопоставить величину потока вектора Пойнтинга с потерям
, составляемого напряженность электрического поля с нормалью к поверхности жилы в точке, принадлежащей поверхности жилы коаксиального кабеля, а также подсчитать величину поток вектора Пойнтинга через боковую поверхность жилы на длине в 1м. и сопоставить величину потока вектора Пойнтинга с потерям
Дата добавления: 2022-05-27; просмотров: 151;










