Более общие волны. Пульсирующая сфера

Вышеизложенное может оставить ложное впечатление, что плоские волны существуют только в трубках, трубах или других ограниченных структурах. Это далеко от правды. Плоские волны могут легко существовать в неограниченных областях. Фактически, акустическое излучение любого источника конечных размеров в конечном итоге приблизится к состоянию плоской волны на достаточно больших расстояниях от источника. Этот эффект мы будем наблюдать в следующем разделе, посвященном простым сферическим волнам.

Пульсирующая сфера. Если бы нас попросили представить простейшую возможную структуру, которая могла бы генерировать звуковые волны в трех измерениях, основываясь только на том, что мы изучили до сих пор, то со всем нашим опытом с детства и далее, мы, вероятно, представим себе пульсирующую, непроницаемую сферическую поверхность. Такая поверхность может иметь номинальный радиус a и будет попеременно то расширяться, то сжиматься, при этом движение будет совершаться вдоль радиальных линий. Ни один громкоговоритель никогда не строился именно таким образом, хотя, если бы он существовал, то он имел бы полезное свойство равномерного излучения во всех направлениях. Представьте себе, что сфера пульсирует на фиксированной частоте f и что радиальная скорость в любой точке поверхности сферы определяется вещественной частью u_me ^j(ωt), где ω = 2πf, а u_m - амплитуда радиальной поверхностной скорости.

В этих условиях альтернативные малые расширения и сокращения сферы будут излучать акустический сигнал на частоте f, которая будет иметь некоторую постоянную среднюю мощность. Поскольку этот сигнал равномерно расходится в пространстве, окружающем пульсирующую сферу, то эта мощность будет расширяться и протекать через концентрические поверхности, имеющие постепенно увеличивающиеся радиусы. Величина мощности постоянна, но площадь, через которую она должна течь, растет со скоростью, пропорциональной квадрату радиального расстояния от центра пульсирующей сферы. В результате интенсивность излучаемого акустического сигнала уменьшается со скоростью, которая обратно пропорциональна квадрату расстояния от начала координат в центре пульсирующей сферы. Интенсивность в целом пропорциональна квадрату акустического давления. Следовательно, амплитуда акустического давления должна уменьшаться обратно пропорционально первой мощности радиального расстояния от начала координат. Другими словами, амплитуда давления на любом расстоянии r при умножении на r является постоянной при любом значении r, равном или превышающем номинальный радиус сферы. В случае плоских волн было обнаружено, что амплитуда давления была постоянной независимо от расстояния от начала координат и что волновое уравнение, определяющее акустическое давление, было:

В рассматриваемом случае сферической волны произведение давления с радиальным расстоянием от начала координат является константой, не зависящей от выбора расстояния от начала координат, поэтому мы предлагаем в качестве волнового уравнения:

где, r - радиальное расстояние от центра пульсирующей сферы, r ≥ a, где a - номинальный радиус пульсирующей сферы.

Решение предложенного волнового уравнения может быть получено с помощью тех же соображений, которые были сделаны в случае плоской волны, если признать, что зависимая переменная теперь является p_r, а не просто p,

где, А - комплексный амплитудный коэффициент, который должен определяться акустическим давлением на поверхности пульсирующей сферы, где r имеет значение а. На этом этапе мы знаем только радиальную скорость на поверхности сферы. Затем необходимо исследовать связь между акустическим давлением и скоростью частицы в случае сферической волны. Когда второй закон Ньютона применялся при выводе случая плоской волны, стало известно, что:

Аналогичное применение к настоящему случаю дает:

Подстановка уравнения 16-82 в левую часть уравнения 16-84 дает:

При решении уравнения 16-85 для отношения акустического давления к скорости частицы получается величина, которая называется удельным акустическим импедансом воздуха для сферических волн.

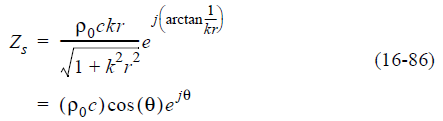
где,

угол θ, как показано на рис. 16-24 представляет разность фаз между акустическим давлением и колебательной скоростью частиц на радиальном расстоянии R от источника,

(ρ₀c) cos (θ) - амплитуда давления, деленная на амплитуду скорости частицы на том же радиальном расстоянии от источника.

Теперь p = Z_su, что означает, что на поверхности сферы, где r = a,

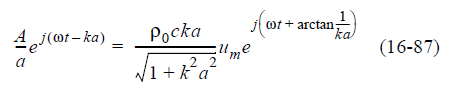
Когда уравнение 16-87, найдено, то A:

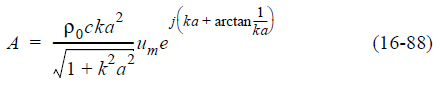
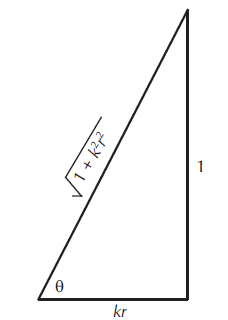
Рисунок 16-24. Угол θ представляет собой угол удельного акустического импеданса воздуха для сферических волн.

Когда это значение A подставляется в уравнение 16-82, то результат становится:

Такое грозное уравнение может вызвать мысли о смене карьеры. К счастью, вопросы могут быть значительно упрощены за счет ограничения внимания пульсирующими шарами, которые малы, так, что ka 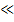1. Желательно это сделать, особенно, когда эту теорию следует применять к звуковым источникам, отличным от сферических источников. Для ka 1,

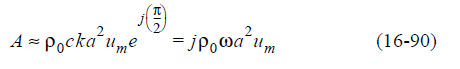
Когда это приближенное выражение для А подставляется в уравнение 16-82, то давление становится:

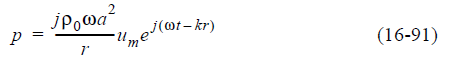
Наконец, полезно ввести площадь излучающего источника, что для сферы радиуса a есть S = 4πa2, так что уравнение 16-91:

Несколько дополнительных слов могут быть полезны здесь в отношении математической техники, используемой в приведенном выше анализе, касающейся реальной физической переменной, такой как акустическое давление или скорость частиц.

В физических ситуациях, когда время t входит в картину в виде гармонической функции, такой как cos (2πft ± α) или cos (ωt ± α), математические операции дифференцирования и интегрирования по времени значительно ускоряются, когда гармоническая функция записывается в сложной экспоненциальной форме. Угол α может быть любым углом или набором углов, которые не зависят от времени, хотя они могут быть частотными. После выполнения необходимых операций фактическая реальная физическая величина получается, если взять только действительную часть конечного комплексного экспоненциального выражения. Примером может служить пример. Напомним теорему Эйлера, что e ^{j (β)} = cos (β) + j sin (β), где β - любой угол, поэтому запишем ведущее j в уравнении 16-92 как e j (π/2) и перепишем уравнение как:

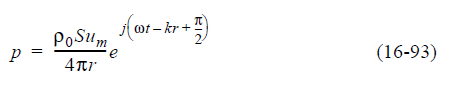
Далее мы разложим уравнение 16-93 по Эйлеру, чтобы получить отдельные вещественные и мнимые части.

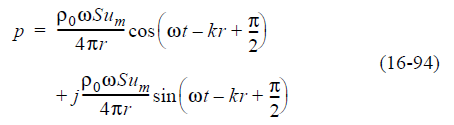
Наконец, только действительная часть уравнения 16-94 описывает фактическое акустическое давление как функцию положения и времени, поэтому:

где, p_m - амплитуда акустического давления, ρ₀ - невозмущенная плотность воздуха, ω - угловая частота, S - площадь поверхности излучающего источника, u_m - амплитуда поверхностной скорости источника, r - радиальное расстояние от источника.

Теперь, когда известно акустическое давление, становится возможным рассчитать скорость частиц воздуха. Специфический акустический импеданс воздуха для сферических волн по своей сути является комплексной величиной, поэтому мы сначала представляем как Zs, так и p(r, t) как комплексные экспоненты и используем тот факт, что:

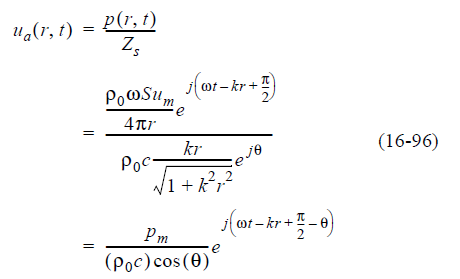
где, u_a (r, t) - скорость частиц воздуха на расстоянии r, p_m - амплитуда акустического давления на расстоянии r, (ρ₀c) cos (θ) - величина удельного акустического импеданса воздуха на расстоянии r.

Физическое значение фактической скорости частицы является лишь реальной частью результата уравнения 16-96 и задается:

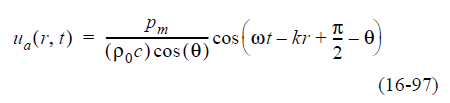
Два вопроса заслуживают внимания при рассмотрении уравнения 16-97. Во-первых, амплитуда скорости частицы представляет собой амплитуду акустического давления, деленную на величину удельного акустического импеданса, а во-вторых, разность фаз между акустическим давлением и скоростью частицы составляет угол удельного акустического импеданса, как показано на рис. 16-24. Когда мы разложим уравнение 16-86, то есть определение удельного акустического импеданса воздуха для сферических волн, в его разделенные вещественные и мнимые части, мы получим:

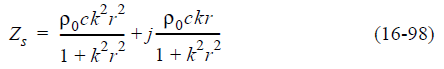
Поскольку наблюдатель приближается к все более отдаленным точкам от простого сферического источника или монополя, как он называется, член k²r² растет все больше и больше по сравнению с одной и вещественной частью уравнения 16-98 приближается к значению ρ₀c. Кроме того, в этих отдаленных областях мнимая часть Z_s становится все меньше и приближается к нулю, в результате чего Z_s приближается к значению, характерному для плоских волн в воздухе, где акустическое давление и скорость частиц находятся в фазе. Поэтому на очень больших расстояниях от простого источника плоские и сферические волны неотличимы при локальных измерениях.