РАЗНОСТНАЯ СХЕМА ЭЙЛЕРА

Рассмотрим задачу Коши: 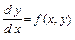; y(a)=y₀. Отрезок [a,b]делим N узлами на шаги (для простоты будем рассматривать равномерное деление)

h = x_k+1 – x_k = (b – a)/N.

Вместо искомой функции y будем рассматривать сеточную функцию y_k, определенную в узлах сетки.

Метод Эйлера основан на разложении искомой функции y(x) в ряд Тейлора в окрестностях узлов, в котором отбрасываются все члены, содержащие производные второго и более высоких порядков:

y(x_k + h) = y(x_k) +y'(x_k)h +o(h²).

Заменяем значения функции y в узлах x_k значениями сеточной функции y_k:

y_k+1 = y_k +y′_kh.

Из исходного уравнения следует, что y′_k = f(x_k,, y_k). Получаем формулу метода Эйлера:

y_k+1 = y_k +hf(x_k, y_k). (6.3)

Локальная погрешность схемы Эйлера (ошибка на одном шаге) равна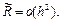

При k=0 y₁ = y₀ +hf(x₀, y₀),

где необходимое значение y₀известно из начального условия.

При k=1: y₂ = y₁ +hf(x₁, y₁) и т.д.

Получаем набор рекуррентных формул, с помощью которых значение сеточной функции у_k+1в любом узле x_k вычисляется по ее значению y_k в предыдущем узле x_k. Поэтому метод Эйлера относят к одношаговым методам.

Какой порядок аппроксимации имеет схема Эйлера?

По определению (см. выше), R_k = f_k – L_k y(x_k). Следовательно, в нашем случае 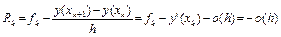, т.е. 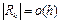. Это означает, что схема Эйлера имеет первый порядок аппроксимации.

Покажем, что схема Эйлера сходится, т.е. 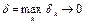при h®0, и имеет первый порядок точности, т.е. 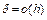. Доказательство будем вести в предположении, что

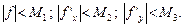
Сразу отметим, что из этих ограничений вытекает следующее:

y″ = f′_x + f′_yy′_x £ M₂ +M₃ M₁ = M₄.

Рассмотрим разность между значением сеточной функции и искомой функции в точках x_k+1, т.е.

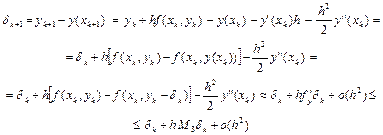
или

.

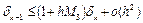Запишем подряд несколько раз это неравенство для разных k, обозначив c=1+hM₃:

d_k £ cd_k–1 + o(h²), d_k–1 £ cd_k–2 + o(h²), …, d₁ £ cd₀+ o(h²)

и выразим d_k через d₀.

d_k £ c²d_k–2 + с×o(h²) + o(h²) £ c³d_k–3 + с²×o(h²) + c×o(h²) + o(h²) £ … £

£ c^kd₀ + с^k–1o(h²) + с^k–2o(h²) +…+ c×o(h²) + o(h²).

В частности, ошибка d_N в конечной точке интервала будет содержать сумму N членов с c^k×o(h²), т.е.

d_N £ c^Nd₀ + N×O(h²)= 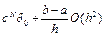=c^Nd₀ + O(h).

Таким образом, если начальные данные заданы точно (т.е. d₀=0), то при h®0 d®0 и d=O(h), т.е. разностная схема Эйлера обеспечивает сходимость с первым порядком точности.

Геометрический смысл схемы Эйлера – замена функции y(x) на отрезке [х_k, х_k+1] отрезком касательной, проведенной к графику в точке х_k (рис.6.1). Из уравнения касательной 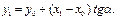По схеме Эйлера .

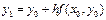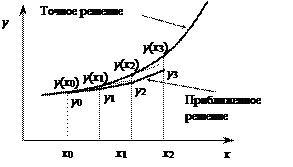Рис.6.1 – Геометрическая интерпретация схемы Эйлера

МЕТОДЫ РУНГЕ-КУТТА

Метод Эйлера является частным случаем широко распространенных в вычислительной практике методов, известных под названием «методы Рунге-Кутта».

Эти методы обладают следующими отличительными свойствами:

1) они являются одношаговыми, т.е. чтобы найти y_k+1,нужна информация только о предыдущей точке: x_k, y_k, и явными (явная зависимость y_k+1 от y_k);

2) они имеют порядок h^p, где p – степень порядка (различна для различных методов);

3) они не требуют вычисления производных от f(x,y), а требуют только вычисления самой функции.

Однако для вычисления одной последующей точки решения приходится вычислять функцию f(x,y) несколько раз при различных значениях x и y. Это та цена, которую приходится платить за право не вычислять никаких производных, но цена более чем умеренная.

Метод Эйлера – метод Рунге-Кутта первого порядка точности. Его медленная сходимость характерна для всех методов первого порядка и служит препятствием для его широкого использования.

Все методы Рунге-Кутта можно представить в виде

y_k+1 = y_k + h j(x_k, y_k)

с соответствующей функцией j. Для метода Эйлера функцией j является сама функция f.

Рассмотрим теперь функцию j, определяемую соотношением

j(x,y) = c₂f(x,y) + c₃f(x+c₁h, y+c₁hf(x,y)).

Попробуем найти наилучшую линейную комбинацию двух значений f (это определяется константами c₂ и c₃) и определим в какой точке интервала при этом следует вычислять второе значение f (это определяется константой c₁) с тем, чтобы максимизировать порядок метода Рунге-Кутта.

Запишем выражение для погрешности аппроксимации:

R = c₂f(x,y) + c₃f(x+c₁h, y+c₁hf(x,y)) –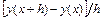

(индекс опустим для простоты).

Выполним серию довольно утомительных преобразований.

1. Разложим функцию j в ряд Тейлора по двум переменным в окрестности точки (x, y): сначала по х, а затем по у.

j(x,y) = c₂f(x,y)+c₃{f(x,y+c₁hf)+с₁hf_x′(x,y+c₁hf)+

+0,5 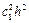f_x″(x,y+c₁hf)+o(h³) } =

=c₂f(x,y)+c₃{f(x,y)+c₁hff_y′(x,y)+0,5 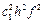f_y″(x,y)+o(h³)+

+c₁h[f_x′(x,y)+c₁hff_xy″(x,y)+o(h²)]+0,5 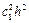[f_x″(x,y)+o(h)]}=

=(c₂+c₃)f+c₁c₃h(ff_y′+f_x′)+0,5c₁²c₃h²(f²f_y″+ +2ff_xy″+f_x″)+o(h³).

2. Разложим точное решение дифференциального уравнения y(x+h) в точке х в ряд Тейлора и преобразуем.

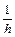[y(x+h) – y(x)] = y′(x)+ 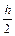y″(x)+ 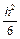y″′(x)+O(h³) = =f+ 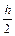f′+ f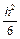″+O(h³).

Совершим ряд вспомогательных действий: найдем полные производные

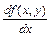и .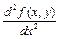

;

.

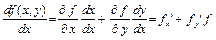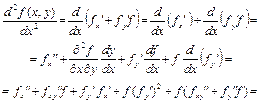
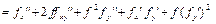Такимобразом,

R = j(x,y) – 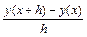= (c₂ +c₃ –1)f + (c₁ c₃ – 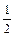)h(ff_y′ +f_x′) +

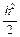+ (c₁²c₃ – 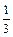)(f²f_y" + 2ff_xy″ + f_x″) – 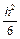(f_x′ f_y′ + f(f_y′)²) – O(h³).

Проанализируем это соотношение.

Для любой функции f, если потребовать с₂ + с₃ = 1; с₁с₃ = 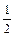, первые два члена обратятся в нуль. Но как бы мы ни выбирали константы, последний член не сможет обратиться в нуль, так что самое большое, что мы можем иметь, это R=o(h²).

Переобозначим: c₃ = s, c₁ = a. Тогда c₂ = 1 – s, .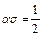

Таким образом, существует однопараметрическое семейство разностных схем второго порядка аппроксимации вида

y_k+1 = y_k +(1– s)hf(x_k,y_k)+ shf(x_k+ ah,y_k +a hf(x_k,y_k)).

Рассмотрим частные случаи:

1. s = 1; a = .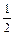

y_k+1 = y_k + hf(x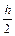_k+ ,y_k + 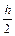f(x_k,y_k)) (6.4)

(модифицированный метод Эйлера).

Геометрическая интерпретация. Через точку А проводится прямая, угловой коэффициент которой равен угловому коэффициенту касательной ВС к интегральной кривой y_B(x), проходящей через промежуточную точку В, построенную по методу Эйлера с шагом h/2 (рис.6.2).

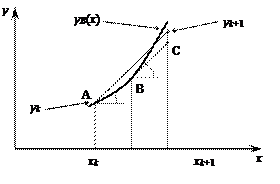Рис.6.2 – Геометрическая интерпретация

модифицированной схемы Эйлера.

2. s = 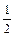; a = 1.

y_k+1 = y_k + 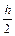[f(x_k,y_k)+ f(x_k+1, y_k + hf(x_k,y_k))] (6.5)

(улучшенный метод Эйлера, метод Хойна).

Геометрическая интерпретация. Через точку А проводится не касательная к интегральной кривой y(x), а прямая AB′ с угловым наклоном, равным средне арифметическому угловых наклонов касательных АВи ВС, которые строятся по методу Эйлера в точках А и В. Решением служит ордината точки В', которая образована пересечением этой прямой с прямой х=х_k+1 (рис.6.3).

Обратите внимание, что эти схемы можно трактовать как схемы «предиктор – корректор» (т.е. «предсказание – уточнение», «счет–пересчет»). Например, в схеме (6.5) сначала по схеме Эйлера делается шаг предиктора и находится 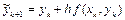, а затем полусуммой делается шаг корректора:

.

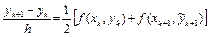Идея схем «предиктор-корректор» очень часто используется при написании разностных схем для уравнений математической физики с частными производными. При этом порядок получающейся схемы выше порядка схемы, используемой на шаге предиктора.

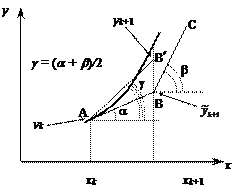Рис.6.3 – Геометрическая интерпретация

улучшенной схемы Эйлера

Без вывода приведем наиболее знаменитую схему метода Рунге–Кутта – классический метод четвертого порядка:

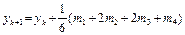, (6.6)

где

m₁ = hf(x_k, y_k); m₂ = hf(x_k + 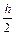, y_k + );

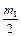m₃ = hf(x_k + 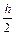, y_k + 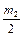); m₄ = hf(x_k+1, y_k + m₃).

Широко используется также модификация классического метода Рунге-Кутта – метод Рунге-Кутта-Мерсона:

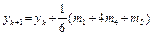; (6.7)

m₁ = hf(x_k,y_k);m₂ = hf(x_k + 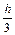, y_k + );

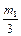m₃ = hf(x_k + 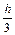, y_k + + );

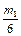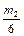m₄ = hf(x_k + 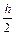, y_k + + );

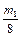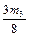m₅ = hf(x_k+1, y_k+ 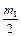– 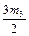+ 2m₄).

Методы Рунге-Кутта без труда переносятся на системы обыкновенных дифференциальных уравнений:

,

; .

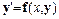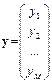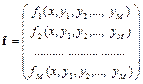Запишем, например, формулы метода Рунге-Кутта 4-го порядка для систем двух уравнений.

.

; .

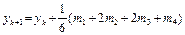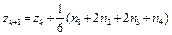m₁ = hj(x_k, y_k, z_k); n₁ = hy(x_k, y_k, z_k);

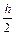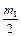m₂ = hj(x_k+ ,y_k+ ,z_k+ 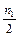); n₂ = hy(x_k + 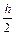, y_k + 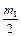, z_k + );

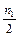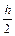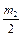m₃ = hj(x_k+ ,y_k+ ,z_k+ 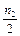); n₃ = hy(x_k + 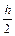, y_k + 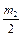, z_k + );

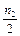m₄ = hj(x_k+1, y_k + m₃, z_k + n₃); n₄ = hy(x_k+1, y_k + m₃, z_k + n₃).

Примечание 1. О построении одношаговых методов высокого порядка.

Наиболее простой, с концептуальной точки зрения, подход к построению одношаговых методов высокого порядка для решения ОДУ заключается в разложении решения в ряд Тейлора. Например,

,

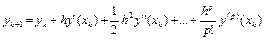где y – точное решение. Легко видеть, что такой метод имеет порядок p. Старшие производные, в принципе, можно определить из самого уравнения (это мы уже делали ранее):

y′(x) = f(x,y); y″(x) = 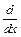f(x,y) = f_x′(x,y) + f_y′(x,y) f(x,y)

и т.д.

Таким образом, при p=1 этот метод является методом Эйлера, а при p=2 принимает вид

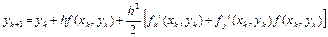
и является методом второго порядка.

Но получение таким образом методов более высокого порядка связано с чрезвычайно громоздкими вычислениями, поэтому они редко используются.

Конец примечания 1.

Примечание 2. О погрешности методов Рунге-Кутта.

Погрешность методов Рунге-Кутта, как и любых методов численного решения задач, складывается из неустранимой погрешности (погрешность математической модели плюс погрешность исходных данных), погрешности метода (в нашем случае она имеет порядок h^p) и вычислительной погрешности, вызванной ошибками округления при проведении расчетов на ЭВМ (она имеет порядок 1/h). Неустранимую погрешность можно уменьшить только за счет более точного определения начальных условий, за счет более точной постановки задачи.

Ошибку аппроксимации мы можем сделать сколь угодно малой за счет уменьшения шага h. Однако чем меньше h, тем больше понадобится шагов на одном и том же интервале [a,b] и, вообще говоря, тем больше скажутся на полученном результате ошибки округления. На практике, когда при выполнении арифметических операций используются ячейки памяти ЭВМ фиксированной длины, всегда существует такая величина шага h=h_*, меньше которой вклад ошибок округления начинает доминировать в суммарной ошибке. Этот минимальный размер шага очень трудно установить заранее. Он меняется от задачи к задаче, от метода к методу (зависит от порядка и от производных M_p).

Из вышесказанного следует, что вычислительный процесс должен быть организован таким образом, чтобы поддерживался баланс между всеми видами погрешности, составляющими полную погрешность решения.

Конец примечания 2.

Рассмотрим практический способ оценки глобальной погрешности метода (правило Рунге). Это апостериорная оценка.

Правило Рунге, которое мы уже использовали ранее при рассмотрении методов численного интегрирования, состоит в том, что решение задачи в некоторой точке x_n находится дважды по одной и той же формуле (например, по формуле Рунге–Кутта) с разными шагами. Обычно в качестве шагов выбирают h и h/2.

Этап I. По формуле Рунге–Кутта с постоянным шагом h находим решение y_h. Оно отличается от точного значения y(x_n).

y(x_n) = y_h + Ah^p + O(h^p+1).

Этап II. Используя ту же формулу с шагом h/2, вычисляем в точке x_n другое значение решения y_h/2, для которого потребуется вдвое больше шагов. Тогда

y(x_n) = y_h/2 + A(h/2)^p + O(h^p+1).

Приравнивая правые части, находим

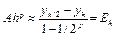. (6.8)

Подставив это значение погрешности, например, во вторую формулу (как более точную), получим повышенную на порядок схему расчета:

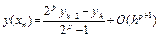. (6.9)

Например, для схемы Эйлера (p=1) эта формула принимает вид:

y(x_n) = 2y_h/2 –y_h +O(h²).

С помощью формулы (6.8) мы можем оценивать погрешность, сравнивая ее с наперед заданной допустимой погрешностью: если |E_h|<e , то заданная точность приближенного решения достигается, если |E_h|>e – нет.

На этом основан алгоритм решения дифференциального уравнения с автоматическим выбором шага: на тех участках изменения независимой переменной, где достигается высокая точность приближенного решения, шаг интегрирования возрастает, а там, где точность не достигается, шаг интегрирования уменьшается до значения, необходимого для ее достижения. Тем самым обеспечивается выбор величины шага в зависимости от характера поведения решения дифференциального уравнения. Необходимо только в алгоритме предусмотреть контроль за количеством деления шага с тем, чтобы не выросла вычислительная ошибка или не появился машинный нуль.