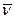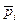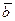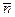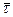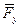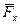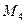Лекции по Динамике.
Динамикой называется раздел механики, в котором изучаются законы движения материальной точки под действием сил.
В динамике наряду с постоянными силами рассматриваются и переменные силы, которые определенным образом зависят от
- времени
- положение тела
- его скорости
Законы сложения и приведения переменных сил те же, что и для постоянных сил.
В основу классической механики положены аксиомы Ньютона.
Основные законы динамики (законы Галилея-Ньютона).
1. Закон инерции.
Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения относительно неподвижной системы отсчета до тех пор, пока действие других тел не изменит ее состояние. (ускорение точки = 0)
Движение при отсутствии сил – движение по инерции.
Инерция – стремление точки сохранить неизменным свое состояние относительно неподвижной системы отсчета. Мерой инерции точки является ее инертная масса (инертная масса = гравитационная масса). Масса зависит от количества вещества, постоянная скалярная величина.
Проявляется свойство инерции в инерциальных системах отсчета (неподвижных, или движущихся равномерно и прямолинейно).
m – масса.
2. Основной закон динамики.
Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной, к ней силе и имеет одинаковое с ней направление.
|
|
|
|



 Основное уравнение динамики
Основное уравнение динамики
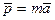
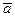 - ускорение
- ускорение
m – инертная масса
Массу тела можно определить по ускорению, которое оно получает под действием известной силы. Например, по силе тяготения.
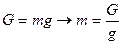
G и g изменяются с изменением широты и высоты над уровнем моря; масса же является величиной неизменной.
3. Закон равенства действия и противодействия.
Две точки действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны.
Всякому действию соответствует равное и противоположно направленное противодействие.
4. Закон независимости действия сил.
(закон суперпозиции сил)
Эта аксиома следует из аксиомы сложения сил, который утверждает.
При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерциальной системы отсчета от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил и полное ускорение равно векторной сумме ускорений от каждой отдельной силы.
Если 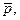 ,
, 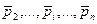 ,
,
то 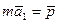 ,
, 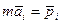 …
…
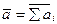
Суммируя, получим
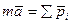 основное уравнение динамики для свободной точки
основное уравнение динамики для свободной точки
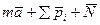 для несвободной точки.
для несвободной точки.
Динамика материальной точки
Задачи динамики для материальной точки.
1) Зная закон движения точки, определить действующую на нее силу.
2) Зная действующую на точку силу, определить закон движения точки.
Эти задачи решают с помощью основного уравнения динамики материальной точки.
|
|


|
|


 m – масса точки
m – масса точки
система сил 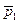 …
… 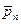
|
|
|
|
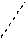

|


Основное уравнение динамики
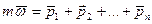
спроектируем обе части этого векторного равенства на координатной оси
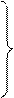 | 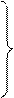 |
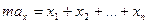
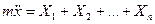
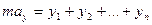
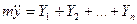
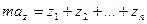
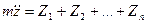
Естественные уравнения движения точки
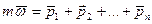
|
|
|
|
|
|







спроектируем на естественные оси
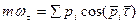
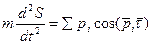
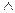
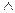
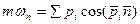
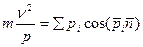
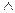
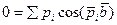
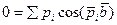
Пример решения первой задачи динамики.
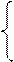 Материальная точка весом 2Н уравнения движения
Материальная точка весом 2Н уравнения движения 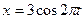 см
см
|
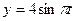 см
см
|
|

 Дифференциальное уравнение движения в векторной форме
Дифференциальное уравнение движения в векторной форме
|
|




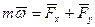
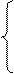 |
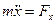
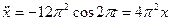
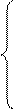
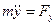
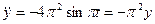
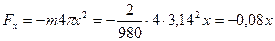
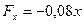
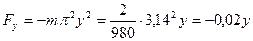
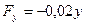
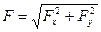 ;
; 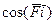
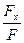
Вторая задача динамики.
 Зная массу, силы, действующие на точку определить закон движения. Возьмем для примера дифференциальные уравнения точки
Зная массу, силы, действующие на точку определить закон движения. Возьмем для примера дифференциальные уравнения точки
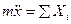
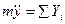
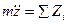
подставляя значение массы и суммы проекции приложенных сил, полученные уравнения дважды интегрируем по времени.
Т.к. силы, действующие на точку в общем случае являются переменными, то правые части уравнений могут зависеть (t, x,y,z, 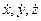 ).
).
Из теории ? дифференциальных уравнений известно, при интегрировании каждого уравнения получаем 2 const, т.к. уравнения 3, то const 3 х 2 будет 6.
Значение const определяется из начальных условий ( 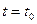 ,
, 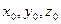 ,
, 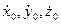 ).
).
 Определив значение const, подставив из заполнения в общее решение уравнения движения точки в виде
Определив значение const, подставив из заполнения в общее решение уравнения движения точки в виде
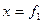 (
( 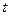 ,
, 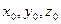 ,
, 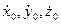 )
)
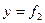 (
( 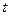 ,
, 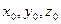 ,
, 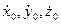 )
)
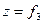 (
( 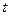 ,
, 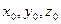 ,
, 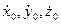 )
)
Уравнения показывают, что под действием одной и той же силы точка может совершать целый класс движений, определяемых начальными условиями движения.
При составлении дифференциальных уравнений за начальный момент времени обычно принимается момент начала движения точки под действием заданных сил, для которого известны как положение точки, так и ее скорость.
Путем введения начальной скорости учитывается влияние на ее движение сил, действующих на материальную точку до того момента, который принят за начальный момент.
Дифференциальные уравнения точки описывают движение точки до тех пор, пока на нее действуют силы, вошедшие в правую часть этих уравнений.
Относительное движение материальной точки.
Два первых закона классической механики и все полученные на их основе уравнения справедливы для движения материальной точки относительно инерциальной системы отсчета.
Рассмотрим движение точки относительно неинерциальной системы отсчета
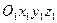 - инерциальная система отсчета
- инерциальная система отсчета
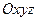 - неинерциальная система отсчета.
- неинерциальная система отсчета.
точка М движется относительно системы отсчета 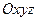 .
.
Движение точки М относительно 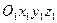 - абсолютное
- абсолютное
Движение точки М относительно 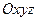 - относительное
- относительное
Будем считать, что переносное движение системы 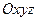 и силы, действующие на точку известны.
и силы, действующие на точку известны.
Основное уравнение динамики для абсолютного движения
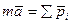 (3.1)
(3.1) 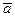 - абсолютное ускорение
- абсолютное ускорение
из кинематики известно:
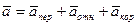
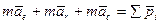 из полученного уравнения определяем
из полученного уравнения определяем 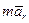
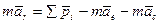 (3.1)
(3.1)
Введем два вектора
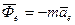
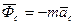
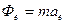
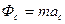
Эти векторы назовем переносной и кориолисовой силой инерции
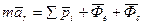
Сравнивая его с основным уравнением для абсолютного движения, можно сказать, что в случае непоступательного переносного движения относительное движение точки можно рассматривать как абсолютное, если к действующим на точку силам присоединить переносную и кориолисову силу инерции.
В инерциальной системе отсчета ускорение точки является результатом действия сил, т.е. взаимодействия с другими телами; в неинерциальной системе отсчета ускорение точки является как результатом действия на нее сил, таки результатом движения самой системы.
Действие сил – динамическая причина возникновения ускорения.
Движение системы – кинематическая причина.
Проектируя векторы уравнения (3.3) на оси подвижной системы получим дифференциальные уравнения относительно движения точки.
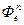 и
и 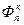 - поправки на неинерциальность системы
- поправки на неинерциальность системы
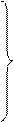
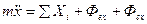
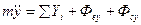
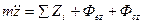
Рассмотрим частные случаи относительного движения точки, соответствующие различным видам переносного движения.
1. Переносное движение – неравномерное вращение вокруг неподвижной оси.
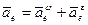
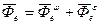
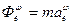 - центробежная сила инерции
- центробежная сила инерции
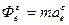 - вращательная сила инерции
- вращательная сила инерции
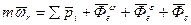
2. Переносное движение – равномерное вращение.
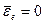
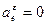
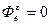
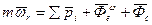
3. Переносное движение – поступательное неравномерное криволинейное
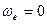
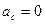
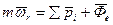
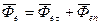
4. Переносное движение – поступательное прямолинейное и равномерное.
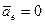
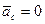
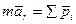
т.е. подвижная система отсчета является в этом случае инерциальной.
Принцип относительности классической механики. Инерциальные системы отсчета.
Уравнение, записанное для случая относительного движения точки по отношению к системе отсчета, движущейся поступательно равномерно и прямолинейно не отличается от основного уравнения динамики.
Таким образом, относительное движение точки по отношению к подвижной системе отсчета, движущейся поступательно прямолинейно и равномерно, происходит также, как и по отношению к неподвижной системе отсчета.
Все таким системы отсчета называются инерциальными системами отсчета, и движение точки относительно любой из этих систем можно рассматривать как абсолютное движение.
Уравнения динамики инвариантны при переходе от одной инерциальной системы к другой.
Наблюдения над относительным движением точки по отношению к любой из таких систем не позволяют определить совершает ли эта система равномерное прямолинейное движение или находится в покое.
Это положение, называемое принципом относительности классовой механики можно сформулировать так.
Никакие механические явления, происходящие в среде, не могут обнаружить ее прямолинейного и равномерного поступательного движения.
Случай относительного покоя.
Рассмотрим случай, когда точка находится в состоянии относительного покоя, т.е. не совершает движения относительно подвижной системы отсчета 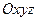 .
.
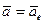 т.к.
т.к. 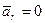
Тогда основное уравнение динамики примет вид
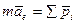 или
или
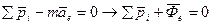
В случае, когда точка находится в состоянии относительного покоя геометрическая сумма приложенных к точке сил и переносной илы инерции равна нулю.
Пример:
Условие относительного покоя на поверхности Земли.
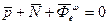
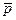 - сила притяжения Земли, направленная к центру;
- сила притяжения Земли, направленная к центру;
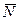 - реакция опоры;
- реакция опоры;
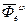 - переносная центробежная сила инерции
- переносная центробежная сила инерции
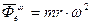 , где
, где 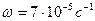 - угловая скорость вращения Земли.
- угловая скорость вращения Земли.
Сложим силы 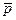 и
и 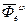 , введем обозначение G
, введем обозначение G
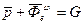
На точку М действуют две силы 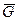 и
и 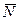 , уравновешивающие друг друга.
, уравновешивающие друг друга.
Сила 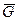 - сила тяжести (вес тела). Направление
- сила тяжести (вес тела). Направление 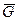 совпадает с направлением вертикали в данной точке земной поверхности.
совпадает с направлением вертикали в данной точке земной поверхности.
Вводя в уравнение равновесия силу тяжести 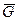 , мы вводим в них силу
, мы вводим в них силу 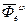 , т.е. учитываем вращение земли, поэтому при составлении уравнений равновесия тела по отношению к Земле никаких поправок на вращение вводить не надо. Равновесие по отношению к Земле можно считать абсолютным.
, т.е. учитываем вращение земли, поэтому при составлении уравнений равновесия тела по отношению к Земле никаких поправок на вращение вводить не надо. Равновесие по отношению к Земле можно считать абсолютным.
Относительное движение вблизи поверхности Земли.
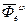 входит в силу тяжести.
входит в силу тяжести.
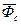 - кориолесова сила инерции.
- кориолесова сила инерции.
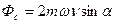
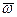 - угловая скорость вращения Земли
- угловая скорость вращения Земли
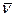 - относительная скорость тела
- относительная скорость тела
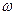 - мала,
- мала, 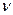 - мала, поэтому
- мала, поэтому 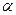 - угол между
- угол между 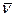 и Земной осью.
и Земной осью.
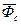 по сравнению с
по сравнению с 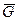 можно пренебречь (
можно пренебречь ( 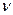 =700 м/с
=700 м/с 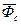 =1% от G).
=1% от G).
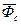 учитывают только при больших относительных скоростях (полет ракет) или для движений длящихся очень долго (течение рек, морские течения).
учитывают только при больших относительных скоростях (полет ракет) или для движений длящихся очень долго (течение рек, морские течения).
Движение по Земной поверхности.
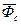 на запад, при движении точки с севера на юг.
на запад, при движении точки с севера на юг.
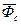 на восток, при движении точки с юга на север.
на восток, при движении точки с юга на север.
В обоих случаях 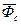 отклоняет точки вправо от движения.
отклоняет точки вправо от движения.
Отсюда заключаем, что в северном полушарии тело, движущееся вдоль земной поверхности по любому направлению, будет вследствие вращения Земли отклоняться вправо от направления движения. (Реки подмывают правый берег. з-н Бэра).
В южном полушарии влево.
В случае вертикального падения тело отклоняется от вертикали к Востоку. Тело, брошенное вертикально вверх, отклоняется к Западу. рисунки
Механическая система.
Системой материальной точки, или механической системой, называют полную совокупность точек, в которой положение и движение каждой точки зависит от положения и движения всех остальных точек.
Систему точек, движение которой не ограничено никакими связями, а определяется лишь действующими на эти точки силами, называют системой свободных точек.
Система точек, движения которых ограничиваются наложенными на точки связями, называют системой несвободных точек.
Механическое действие связей на точки системы выражаются реакциями связей. Таким образом, все силы, действующие на систему несвободных точек, можно разделить на задаваемые (активные) и реакции связей.
Все силы, действующие на точку как свободной, так и несвободной механической системы можно разделить и по-другому признаку: на внешние и внутренние.
Внешними называют силы, действующие на точку системы со стороны точек, не входящих в состав данной системы.
Внутренними называются силы взаимодействия между точками данной механической системы.
Внешние - 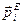
Внутренние - 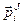
Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того, какая механическая система рассматривается. (Движение всей солнечной системы в целом, то сила притяжения к солнцу – внутренняя, при изучении движения Земли, она уже внешняя).
Как внешние, так и внутренние силы могут быть в свою очередь активными, или реакциями связей.
Свойства внутренних сил механической системы.
1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю.
По третьему закону динамики
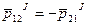
аналогичный результат для любой пары точки.
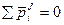
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси = 0.
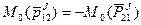
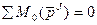
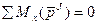
Однако, не следует, что внутри силы взаимно уравновешиваются и не влияют на движение системы.
Эти силы приложены к разным точкам механической системы и могут вызывать взаимное перемещение точек системы.
Дифференциальные уравнения движения механической системы.
Система точек
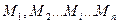 .
.
обозначим массу каждой точки 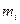 , и в каждую точку проведем
, и в каждую точку проведем 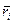
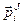 ,
, 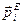 равнодействие, приложенных к i-точке внутренних и внешних сил.
равнодействие, приложенных к i-точке внутренних и внешних сил.
основное уравнение динамики
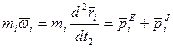 (i = 1… n)
(i = 1… n)
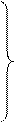 спроектируем его на координатной оси.
спроектируем его на координатной оси.
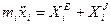
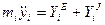 (4.1) дифференциальные уравнения движения
(4.1) дифференциальные уравнения движения
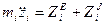 механической системы
механической системы
Проинтегрировать эти уравнения удается лишь в исключительных случаях. Основная их роль состоит в том, что они или следствия из них, являются исходными для получения общих теорем динамики.
Центр масс механической системы и его координаты. Твердое тело.
Каждая точка 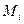 имеет определенную массу
имеет определенную массу 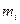 и положение относительно
и положение относительно 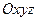 определяется
определяется 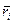 или
или 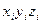 .
.
Центром масс называется геометрическая точка с, радиус-вектор который
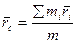
где 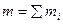 масса всей системы.
масса всей системы.
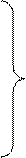 Проектируя (4.2) на координатной оси.
Проектируя (4.2) на координатной оси.
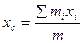
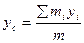 (4.3)
(4.3)
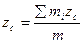
Вывод. Центр масс является не материальной точкой, а геометрически он может не совпадать ни с одной из материальных точек системы (кольцо).
Центр масс характеризует распределение масс в системе.
Из формул (4.3), (4.2) видно, что положение центра масс системы зависит только от положения и массы каждой точки этой системы.
Центр тяжести тел является центром масс этой системы.
(Статика) 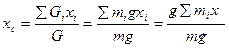
Понятие «центр масс» применимо для любой системы материальной точки, тогда как понятие «центр тяжести» применяется лишь для механических систем, находящихся в однородном поле силы тяжести.
Твердое тело.
Рассмотрим систему точек, расстояние между которыми не меняется. Такая система называется неизменяемой.
|
|
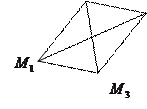 |
Для образования неизменной системы каждую точку нужно соединить идеальными стержнями по крайней мере с тремя точками, уже входящими в неизменную систему.
Считая число точек неизменяемой системы бесконечно большим, а длины соединяющих их идеальных стержней бесконечно малыми, получаем модель абсолютно твердого тела.
Теорема о движении центра масс.
( 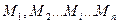 )
)
Уравнения движения этих точек
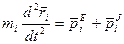 (i = 1, 2 … n)
(i = 1, 2 … n)
Суммируем эти уравнения.
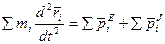
Преобразуем левую часть равенства
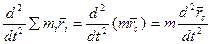
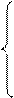 т.к.
т.к. 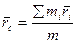 Получаем:
Получаем:
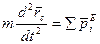 или
или
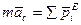
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил.
Уравнение выражает теорему о движении центра масс системы, которая формируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
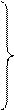 Проектируя (4.5) на координатные оси
Проектируя (4.5) на координатные оси
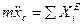 Это дифференциальные уравнения движения центра
Это дифференциальные уравнения движения центра
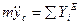 масс системы
масс системы
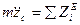
Следствия из теоремы
1. Если 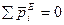 , то центр масс механической системы находится в покое, или движется равномерно и прямолинейно.
, то центр масс механической системы находится в покое, или движется равномерно и прямолинейно.
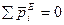 ,
, 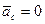 , т.е.
, т.е. 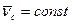 .
.
2. Если 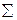 проекций внешних сил на какую-либо ось равна нулю, то проекция центра масс механической системы на эту ось или неподвижна или движется равномерно.
проекций внешних сил на какую-либо ось равна нулю, то проекция центра масс механической системы на эту ось или неподвижна или движется равномерно.
Пусть 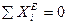 , тогда
, тогда 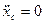 , т.е.
, т.е. 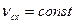 , если при этом в начальный момент
, если при этом в начальный момент 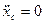 , то
, то 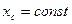 .
.
Дифференциальные уравнения поступательного движения твердого тела.
При поступательном движении все точки тела движутся как его центр масс. Поэтому дифференциальные уравнения движения центра масс механической системы являются дифференциальными уравнениями поступательного движения твердого тела.
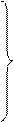
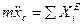
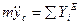
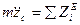
m – масса тела
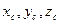 координаты центра масс.
координаты центра масс.
(С помощью этих уравнений решаются 2 задачи динамики).
Таким образом, изучение поступательного движения твердого тела сводится к изучению движения отдельной материальной точки, имеющей массу всего тела.
Импульс силы.
Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени вводится понятие об импульсе силы.
Элементарным импульсом силы называется векторная величина 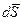 , равная произведению вектора силы
, равная произведению вектора силы 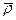 на элементарный промежуток времени dt:
на элементарный промежуток времени dt:
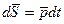 .
.
Импульс силы 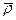 за конечный промежуток
за конечный промежуток 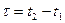
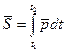
Импульс силы характеризует передачу точки механического движения со стороны, действующих на нее тел за данный промежуток времени.
Если 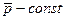 (частный случай), то
(частный случай), то 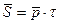 (4.10)
(4.10)
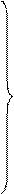 Найдем проекции
Найдем проекции 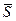 на координатные оси.
на координатные оси.
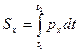 По этим проекциям можно найти сам вектор
По этим проекциям можно найти сам вектор 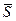
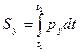
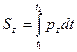
Импульс равнодействующей нескольких сил за некоторый промежуток времени равен геометрической сумме импульсов составляющих сил за тот же промежуток времени.
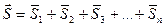
Теорема об изменении количества движения материальной точки.
Количеством движения материальной точки называется вектор, имеющий направление скорости и модуль, равный произведению массы точки на модуль скорости ее движения.
Количество движения точки зависит от ее массы и скорости, является мерой механического движения.
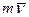 - количество движения.
- количество движения.
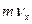 ,
, 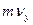 ,
, 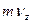 - проекции количества движения на координатной оси.
- проекции количества движения на координатной оси.
Р – равнодействующая, приложенных к точке сил.
Основное уравнение динамики преобразуем следующим образом.
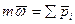 или
или 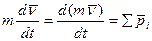
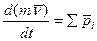
Уравнение (5.8) выражает теорему об изменении 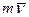 в дифференциальной форме:
в дифференциальной форме:
Производная по времени от количества движения точки геометрически равна равнодействующей приложенных к точке сил.
Запишем уравнение (5.8) в виде
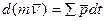 и проинтегрируем в пределах, соответствующих моментов времени
и проинтегрируем в пределах, соответствующих моментов времени 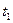 и
и 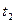
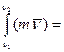
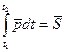 , получим
, получим
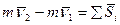
Заменим в уравнении (5.9) импульс равнодействующими импульсами составляющих сил.
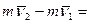
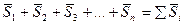
Уравнение (5.10) выражает теорему об изменении количества движения материальной точки в конечной форме:
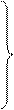 Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени (теорема импульсов).
Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени (теорема импульсов).
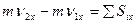
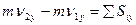
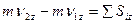
Изменение проекции количества движения точки на данную ось за некоторый промежуток времени равно сумме проекции на ту же ось импульсов, приложенных к точке сил, за то же промежуток времени.
Количество движения механической системы.
Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количественного движения всех материальных точек этой системы
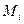 (i = 1, 2, …, n)
(i = 1, 2, …, n) 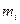 и
и 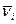 , то
, то
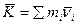
Преобразуем это выражение.
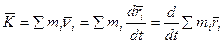
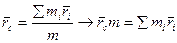 ;
;
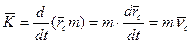
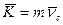
Вектор количества движения механической системы равный произведению массы системы на скорость ее центра масс, имеет направление скорости:
Проектируем (6.2) на координатные оси.
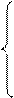
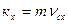
(6.3) 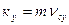
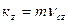
Продифференцируем (6.2) по времени
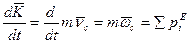
(6.4) 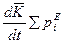 Теорема об изменении
Теорема об изменении 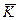 в дифференциальной форме.
в дифференциальной форме.
Производная по времени от 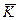 равна главному вектору внешних сил.
равна главному вектору внешних сил.
Уравнению (6.4) соответствуют 3 уравнения в проекциях на оси координат
(6.5) 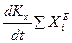 ,
, 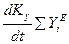 ,
, 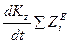
Из уравнений (6.4) и (6.5) следует, что изменение 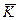 вызывается только внешними силами.
вызывается только внешними силами.
Следствия из теоремы:
1) Если за рассматриваемый промежуток времени, то количество движения механической системы const.
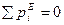 , то
, то 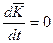 , т.е.
, т.е. 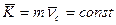 .
.
2) Если 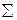 проекций внешних сил равна нулю на какую-либо ось за рассматриваемый промежуток времени, то проекция
проекций внешних сил равна нулю на какую-либо ось за рассматриваемый промежуток времени, то проекция 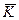 на эту ось постоянна
на эту ось постоянна
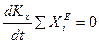 , то
, то 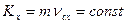 .
.
Найдем связь между изменение К и импульсами действующих на эту систему счисления.
Для каждой точки м. с можно определить изменение количества движения за промежуток 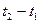 (формула 5.9).
(формула 5.9).
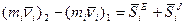 (i = 1…n).
(i = 1…n).
Суммируем правые и левые части уравнений.
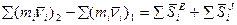 по свойству внутренних сил.
по свойству внутренних сил.
Получаем:
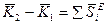 (6.6) – Теорема об изменении количества движения механической системы в интегрированной (конечной) форме.
(6.6) – Теорема об изменении количества движения механической системы в интегрированной (конечной) форме.
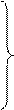 Изменение
Изменение 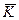 за некоторый промежуток времени равен геометрической сумме импульсов внешних сил за тот же промежуток времени.
за некоторый промежуток времени равен геометрической сумме импульсов внешних сил за тот же промежуток времени.
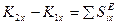
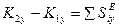 (6.7)
(6.7)
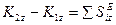
Изменение проекции количества движения механической системы на любую ось равно сумме проекции импульсов всех внешних сил, действующих на систему, на ту же ось.
Момент количества движения материальной точки
относительно центра и относительно оси.
Вычисляется момент вектора 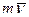 так же, как и момент силы.
так же, как и момент силы.
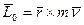
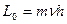 .
.
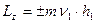
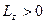 , если можно видеть, смотря навстречу оси,
, если можно видеть, смотря навстречу оси,
| <== предыдущая лекция | | | следующая лекция ==> |
| Эволюция объектов мониторинга в космической отрасли | | | Способы задания движения. |
Дата добавления: 2016-06-29; просмотров: 1439;