Теорема Форда – Фалкерсона.

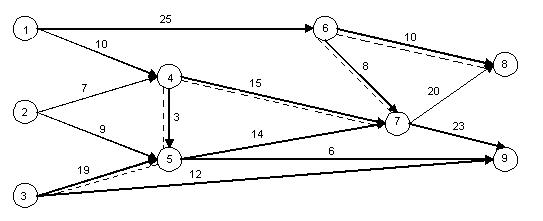
Алгоритм решения задачи о максимальном потоке основан на теореме Форда – Фалкерсона о максимальном потоке и минимальном разрезе. Для рассмотрения этой теоремы вводятся понятияо прямой и обратной дуги цепи. Под цепью в данном случае понимается последовательность сцепленных дуг сети без учёта их ориетации. Дугу, принажлежащую некоторй цепи, называют прямой, если её направление совпадает с направлением обхода узлов этой цели, и обратной - в противном случае например, цепь µ=(3,5,4,7,6,8) на рис.1, связывающая узел 3 с вершиной 8, содержит три прямые дуги (3,5), (4,7), (6,8) и две обратные (4,5), (6,7).

Теорема. В любой сети максимальная величина потока из источника в сток равна пропускной способности минимального разреза сети.

Доказательство. Пусть имеем максимальный поток в сети. Если x_ij=d_ij, то говорят, что дуга (i,j) насыщена потоком. Предполагается, что V^* величина максимального потока в сети. Необходимо доказать, что найдется такой разрез (R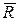^*, ^*) на этой сети, пропускная способность которого равна V^* , т.е. V ^*= d(R^*, ^*).

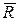Такой разрез можно построить, если в подмножество R включить все узлы, которые достигаются по некоторой цепи из истока, а в подмножество 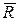– все остальные вершины .

Узлы , составляющие подмножество R , определяются последовательно , начиная с источника Ø , по следующему правилу : Ø = R ; если 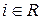и x_ij < d_ij

то 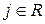; если 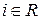и x_ji >0, то 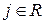. (4)

Применение правила (4) приводит к построению разреза. Очевидно, разрез будет построен в том случае , если сток .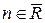

Пусть сток 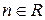. Тогда из правила (4) следует , что существует цепь из истока Ø в сток n с пропускной способностью больше нуля µ=(i₁,i₂,…,i_n), где i₁= Ø, i_n=n. Это следует из того , что все прямые дуги , входящие в цепь, ненасыщенные (xi_si_s+1< di_si_s+1 ), а для всех обратных дуг ( i_s+1,i_s ) величина потока xi_s+1i_s>0.

Пусть δ₁ наименьшая разность между пропускной способностью и величиной потока, взята по всем прямым дугам цепи µ , а δ₂ - наименьшая величина потока, взятая по всем обратным дугам этой цепи. Далее определяется величина δ= min(δ₁, δ₂) > 0 и увеличивается поток по всем прямым дугам цепи на δ ,а на ту же величину уменьшается поток по всем обратным дугам цепи. Таким образом, величина нового потока равна V+ δ , что противоречит предположению о максимальности V . Следовательно предположение 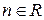неверно, и 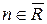, а множество дуг (R, 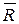) есть разрез, отделяющий исток от стока.

Пропускная способность построенного разреза равна максимальному потоку на сети. Действительно, из правила (4) нахождения подмножества R следует , что если

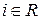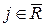, , то x_ij = d_ij ; в противном случае узел j входил бы в R.

Таким образом,

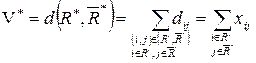
Теорема доказана.