Типы сходимостей итерационных последовательностей

Итерационные численные методы решения уравнений с одним неизвестным

Отделение корней

Будем рассматривать задачу приближенного нахождения нулей функции одной переменной, иначе, задачу нахождения корней уравнения вида

f(x) = 0, (1)

где f: R ® R — алгебраическая или трансцендентная функция.

В общем случае, если речь идет не об отдельных достаточно узких классах уравнений, например, изучавшихся в школьном курсе математики, можно говорить лишь о приближенном вычислении корней уравнений (1), т.е. таких значений аргумента x = ξ, при которых равенство

f(ξ) = 0

истинно. При этом под близостью приближенного значения x к корню ξ уравнения (1), как правило, понимают выполнение неравенства

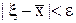
при малых ε > 0, хотя часто бывает важным контролировать не абсолютную погрешность приближенного равенства 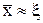, а относительную, т.е. величину 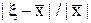, например, когда величина 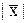близка к нулю.

Если функция f(x) такова, что без особого труда можно построить ее график, этим следует воспользоваться, чтобы представить ситуацию с количеством и расположением нулей f(x) выделяя те промежутки оси абсцисс, где график у = f(x) пересекает Ox. (Знание графика много дает и для понимания поведения тех или иных процессов вычисления приближений к корням.) Может оказаться, что построение графика у = f(x) вызывает затруднения, но исходное уравнение (1) очевидным образом представляется в виде

f₁(x) = f₂(x)

и функции f₁(x) и f₂(x) таковы, что легко строятся графики у = f₁(x) и у = f₂(x). Тогда задача определения количества корней и областей их единственности решается отслеживанием точек пересечения этих графиков и выделением на оси абсцисс тех промежутков, которым принадлежат проекции таких точек. Описанный прием называют графическим способом локализации (иначе, отделения, изоляции) корней.

Убедиться в том, что на данном отрезке [а, b] (например, грубо определенном графическим способом) действительно имеется нуль непрерывной функции f(x), можно аналитическим способом, в основе которого лежит известное утверждение математического анализа.

Теорема 1. Больцано-Коши.

Если непрерывная на отрезке [а, b] функция f(x) на концах его имеет противоположные знаки, т.е.

f(a)f(b) < 0, (2)

то на интервале (а, b) она хотя бы один раз обращается в нуль.

Метод дихотомии

Пусть функция f(x) определена и непрерывна при всех xÎ[a;b] и на [а;b] меняет знак, т.е. f(a)f(b) < 0. Тогда согласно Теорема 1 уравнение (1) имеет на (а;b) хотя бы один корень. Возьмем произвольную точку c Î (а;b). Будем называть в этом случае отрезок [а;b] промежутком существования корня, a точку с — пробной точкой. Поскольку речь здесь идет лишь о вещественнозначных функциях вещественной переменной, то вычисление значения f(c) приведет к какой-либо одной из следующих взаимоисключающих ситуаций:

а) f(а)f(с) < 0; б) f(с)f(b) < 0; в) f(с) = 0. Применительно к рассматриваемой задаче их можно интерпретировать так:

а) корень находится на интервале (а; с);

б) корень находится на интервале (с; b);

в) точка c является искомым корнем.

Таким образом, одно вычисление значения функции позволяет уменьшить промежуток [а; b] существования корня (ситуация а) или б)) или указать его значение (ситуация в), маловероятная в смысле «прямого попадания» пробной точкой с в корень, но вполне реальная в смысле выполнения приближенного равенства f(с) » 0, когда длина промежутка существования корня близка к длине промежутка его неопределенности). Ясно, что в зависимости от того, имеет место ситуация а) или б), описанная процедура одного шага сужения промежутка существования нуля непрерывной функции f(x) может быть применена к промежутку [a; c] Ì [a; b] или к [c; b] Ì [a; b] соответственно и далее повторяться циклически. Такой простой и легко программируемый процесс называется методом дихотомии. Если способ задания пробных точек с определен так, что последовательность длин получающихся в этом процессе промежутков существования корня стремится к нулю, то методом дихотомии можно найти какой-либо корень уравнения (1) с наперед заданной точностью.

Наиболее употребительным частным случаем метода дихотомии является метод половинного деления, реализующий самый простой способ выбора пробной точки — деление промежутка существования корня пополам. Выполнить приближенное вычисление с точностью ε корня уравнения (1) методом половинного деления при условии, что f(x) непрерывна на [а; b] и f(а)f(b) < 0, можно, например, по следующей схеме:

Шаг 0. Задать концы отрезка а и b, функцию f, малое число ε > 0 (допустимую абсолютную погрешность корня или полудлину его промежутка неопределенности), малое число d > 0 (допуск, связанный с реальной точностью вычисления значений данной функции); вычислить (или ввести) f(а).

Шаг 1. Вычислить с = 0.5(а + b).

Шаг 2. Если b – a < 2e, положить ξ » a (ξ — корень) и остановиться.

Шаг 3. Вычислить f(с).

Шаг 4. Если |f(с)| < δ, положить ξ » c и остановиться.

Шаг 5. Если f(а)f(с) < 0, положить b = с и вернуться к шагу 1; иначе положить а = с, f(a) = f(c) и вернуться к шагу 1.

За один шаг метода половинного деления промежуток существования корня сокращается ровно вдвое. Поэтому, если за k-e приближение этим методом к корню ξ уравнения (1) примем точку x_k, являющуюся серединой полученного на k-м шаге отрезка [a_k, b_k] в результате последовательного сужения данного отрезка [а, b], полагая a₁ = а, b₁ = b, то придем к неравенству

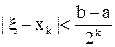"k Î N (3)

(априори, ξ — любая точка интервала (a_k, b_k), и расстояние от нее до середины этого интервала не превосходит половины его длины. Это как раз и видим в (3) при k = 1).

Неравенство (3), с одной стороны, позволяет утверждать, что последовательность (x_k) имеет предел — искомый корень ξ уравнения (1); с другой стороны, являясь априорной оценкой абсолютной погрешности приближенного равенства x_k » ξ, дает возможность подсчитать число шагов (итераций) метода половинного деления, достаточное для получения корня ξ с заданной точностью ε, для чего нужно лишь найти наименьшее натуральное k, удовлетворяющее неравенству

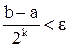
Используемый в методе половинного деления способ фиксирования пробной точки можно охарактеризовать как пассивный, ибо он осуществляется по заранее жестко заданному плану и никак не учитывает вычисляемые на каждом шаге значения функции. Логично предположить, что в семействе методов дихотомии можно достичь несколько лучших результатов, если отрезок [а; b] делить точкой c на части не пополам, а пропорционально величинам ординат f(a) и f(b) графика данной функции f(x). Это означает, что точку с есть смысл находить как абсциссу точки пересечения оси Ox с прямой, проходящей через точки A(а; f(a)) и B(b; f(b)), иначе, с хордой АВ дуги ΑξΒ (Рис. 1).

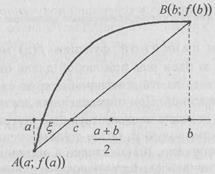
Рис. 1. Дуга графика функции f(x) и стягивающая ее хорда

Запишем уравнение прямой, проходящей через две данные точки A к B:

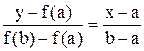
Отсюда, полагая у = 0 (уравнение оси Ох), x = с (обозначение искомой точки пересечения прямой АВ с осью Ох), находим

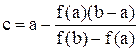(4)

Метод, получающийся в развитие метода дихотомии таким фиксированием пробной точки, называют методом хорд.

Типы сходимостей итерационных последовательностей

Чтобы более объективно судить о скорости сходимости тех или иных итерационных методов, введем следующие понятия.

Пусть некоторый итерационный процесс генерирует последовательность 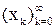, имеющую пределом x*.

Определение 1. Линейная и сверхлинейная сходимость.

Сходимость последовательности (x_k) к x* называется линейной (соответственно, итерационный процесс — линейно сходящимся), если существует такая постоянная C Î (0; 1) и такой номер k₀, что

|x* – x_k+1| £ C|x* – x_k| " k ³ k₀ (5)

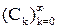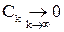и сверхлинейной, если существует такая положительная последовательность , что и

|x* – x_k+1| £ C_k|x* – x_k| " k Î N₀ (6)

Определение 2. Сходимость порядка p.

Говорят, что последовательность (x_k) сходится к x* по меньшей мере с p-м порядком (соответственно, итерационный процесс имеет по меньшей мере p-й порядок), если найдутся такие константы C > 0 и p ³ 1, что

|x* – x_k+1| £ C|x* – x_k|^p (7)

при всех k Î N₀, начиная с некоторого k = k₀.

Фиксируя в Определение 2 значение p = 1, видим, что линейно сходящийся процесс можно называть процессом первого порядка, значению p = 2 в (7) соответствует квадратично сходящийся процесс, p = 3 означает кубическую сходимость.

Метод ньютона

Для простоты будем считать, что функция f(x) дважды дифференцируема на отрезке [а, b], содержащем корень ξ уравнения (1).

Пусть x_k Î [a; b] — уже известный член последовательности приближений к ξ, полученный конструируемым методом (или заданное начальное приближение x₀ при k = 0). Для любого x из [а, b] можно записать формальное представление f(x) по формуле Тейлора

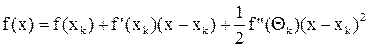, (8)

где Q_k Î [a;b] — некоторая точка между x и x_k.

Так как корень ξ — потенциально произвольная точка отрезка [а, b], то разложение (8) справедливо и для x = ξ, т. е. существует точка 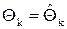такая, что

.

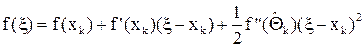Но f(ξ) = 0, и если точка 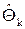известна, то корень ξ можно точно найти из квадратного уравнения

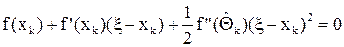(9)

Считая, что значение x_k близко к ξ, т.е. разность ξ – x_k по модулю достаточно мала, можно рассчитывать, что величина (ξ – x_k)² будет тем более малой. На этом основании отбросим в (9) последнее слагаемое и подменим квадратное уравнение (9) линейным уравнением. Естественно, что при этом будет найден не корень ξ, а некоторая другая точка, которую обозначим x_k+1.

Таким образом, итерационный процесс Ньютона определяется линейным уравнением

f(x_k) + f'(x_k)(x_k+1 – x_k) = 0 (10)

или в явном виде формулой

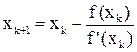, (11)

где k = 0, 1, 2, ... и предполагается, что по крайней мере на элементах последовательности (x_k) первая производная данной функции в нуль не обращается.

Если в равенстве (10) фиксированную точку x_k+1 заменить переменной x, а 0 в правой части — переменной у, то в полученном легко узнать уравнение касательной к кривой y = f(x), проведенной к ней в точке (x_k; f(x_k)). Отсюда геометрический смысл метода Ньютона: приближения к корню ξ совершаются по абсциссам точек пересечения касательных к графику данной функции, проводимых в точках, соответствующих предыдущим приближениям (Рис. 2).

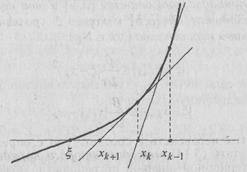
Рис. 2. Геометрический смысл метода Ньютона

Теорема 2. Апостериорная погрешность метода Ньютона.

Пусть функция f(x) удовлетворяет условиям

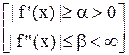"x Î [a; b] (12)

Тогда, если члены последовательности (x_k), определяемые методом Ньютона (11), при любом фиксированном k Î N₀ принадлежат отрезку [а, b] и эта последовательность сходится на [а, b] к корню ξ уравнения (1), то справедливы неравенства ("k Î N₀):

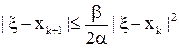(13)

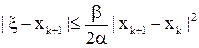(14)

(Первое из этих неравенств в соответствии с Определение 2 позволяет считать (11) методом второго порядка, а второе, являясь апостериорной оценкой погрешности, может служить в качестве критерия останова процесса вычислений).

Теорема 3. Априорная погрешность метода Ньютона.

Пусть для функции f(x) на отрезке [а, b] выполнены условия (12).

Тогда, если интервал 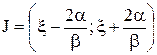содержится в [а, b], то при произвольном выборе x₀ из J для определяемой методом Ньютона (11) последовательности (x_k):

1) x_k Î J "k Î N;

2) 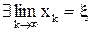и f(ξ) = 0;

3) справедливо утверждение Теорема 2 и оценка

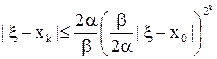. (15)

Теорема 4. Условия сходимости метода Ньютона.

Пусть на отрезке [а,b] функция f(x) имеет первую и вторую производные постоянного знака и пусть

f(а)f(b) < 0.

Тогда, если точка x₀ выбрана на [а, b] так, что

f(x₀)f"(x₀) > 0, (16)

то начатая с нее последовательность (x_k), определяемая методом Ньютона (11), монотонно сходится к корню ξ Î (a; b) уравнения (1).

Цель всех последующих видоизменений основной формулы (11) метода Ньютона — уменьшение вычислительных затрат, связанных с необходимостью вычисления производной на каждом итерационном шаге.

На получение сверхлинейной скорости сходимости при видоизменении метода Ньютона (11) можно надеяться в случае, когда f'(x_k) при каждом k Î N подменяется некоторым близким к f'(x_k) значением, которое может быть найдено (при каждом k свое) через значения данной функции. Для таких аппроксимаций f'(x_k) можно использовать, например, определение производной. Имеем:

,

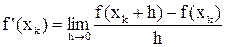и при малых h (произвольного знака) получаем приближенное равенство

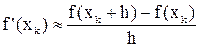, (17)

позволяющее производную приближенно подменять так называемым разностным отношением. Подстановка (17) в (11) приводит к итерационной формуле

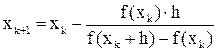(18)

где k = 0, 1, 2, ..., a h — малый параметр, которым должен распорядиться вычислитель.

Ясно, что при каждом k в формуле (17) может быть свое значение h, т.е. в формуле (18) вместо постоянного параметра h имеет смысл использовать связанный с номером итерации параметр h_k, т.е. вести вычисления по формуле

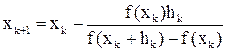(19)

Итерационный метод, определяемый формулами (18) или (19), назовем разностным методом Ньютона.

Так как равенство (17) можно сделать сколь угодно точным за счет малости шага h разностного отношения (теоретически; практически это далеко не так из-за потерь точности при вычитании близких чисел), то по непрерывности можно утверждать асимптотически квадратичную скорость сходимости разностного метода Ньютона при определенных условиях.

Опираясь на то, что необходимым условием сходимости некоторой последовательности x_k к пределу ξ является сходимость к нулю последовательности разностей x_k – x_k–1 (причем с той же скоростью), положим в (19)

h_k = x_k–1 – x_k, откуда x_k–1 = x_k + h_k. В результате этого из (19) получаем итерационный процесс

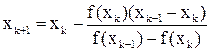, (20)

где k = 1, 2, 3, ..., а x₀ и x₁ должны задаваться.

Формула (20) определяет новый метод как двухшаговый (результат (k + 1)-го шага зависит от результатов k-гo и (k – 1)-го шагов) и на каждой итерации требует вычисления только одного значения функции, другое же значение, фигурирующее в этой формуле, передается с предыдущего шага. Сравнив (20) с формулой (4), полученной из геометрических соображений, легко понять, что x_k+1 есть абсцисса точки пересечения с осью Ox прямой, проведенной через точки (x_k–1, f(x_k–1)) и (x_k; f(x_k)), т.е. секущей (Рис. 3). Отсюда название этого метода — метод секущих.

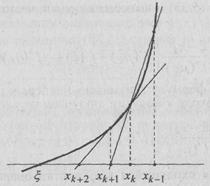
Рис. 3. Приближения к корню методом секущих