Соединяющей эти точки
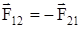 .
.
Эти силы приложены к разным материальным точкам (телам), всегдадействуют парами и являются силами одной природы. Закон справедлив для описания взаимодействия покоящихся тел, а также в случае контактных взаимодействий.
Пример: Пусть тело массой m лежит на горизонтальной поверхности.
Тело действует на нее с силой 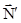 , направленной вертикально вниз. Поверхность же действует на тело с силой (реакция опоры), равной по модулю силе
, направленной вертикально вниз. Поверхность же действует на тело с силой (реакция опоры), равной по модулю силе 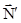 . На тело также действует сила тяжести. Так как тело находится в покое то, очевидно, = - и все эти силы равны по модулю (рис.2.2.).
. На тело также действует сила тяжести. Так как тело находится в покое то, очевидно, = - и все эти силы равны по модулю (рис.2.2.).
2. 3. Закон сохранения импульса. @
Рассмотрим общий случай - систему n взаимодействующих материальных точек (тел). На каждое тело действуют внутренние и внешние силы. Силы взаимодействия между телами системы называются внутренними, а силы, которые действуют со стороны тел, не входящих в рассматриваемую систему, называются внешними. Массы точек - m1, m2, ..., mn, скорости их движения - v1, v2,...,vn. Пусть 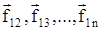 - внутренние силы, действующие на первую точку со стороны второй, третьей и т.д.
- внутренние силы, действующие на первую точку со стороны второй, третьей и т.д. 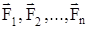 - внешние силы, действующие на первую, вторую и т.д. материальные точки (рис.2.3.).
- внешние силы, действующие на первую, вторую и т.д. материальные точки (рис.2.3.).
Так как внутренние силы являются силами взаимодействия между телами, то они должны подчиняться третьему закону Ньютона 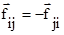 .
.
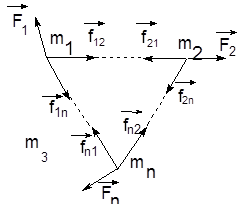 Рис.2.3. Силы взаимодействия в системе n материальных точек.
Рис.2.3. Силы взаимодействия в системе n материальных точек.
|
Запишем II закон Ньютона для каждого из n тел:
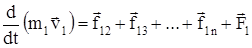
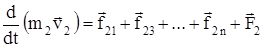
. . . . . .
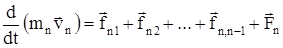 .
.
Если просуммировать эти уравнения по всем телам и учесть, что при двойном суммировании внутренних сил, согласно третьему закону Ньютона
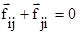 , то получаем
, то получаем 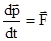 , где
, где 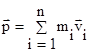 ,
, 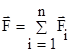 .
.
Если система замкнутая, т.е. на нее не действуют внешние силы, то 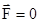 ,
, 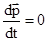 , т.е.
, т.е. 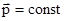 .
.
Это выражение является законом сохранения импульса. Суммарный импульс замкнутой системы точек (тел) не меняется с течением времени.
Закон сохранения импульса находит широкое применение в природе и технике. Примером может служить явление отдачи ружья при выстреле пули. Выстрел производится в горизонтальном направлении (рис.2.4).
 Систему ружье-пуля можно считать изолированной системой и к ней применим закон сохранения импульса:
Систему ружье-пуля можно считать изолированной системой и к ней применим закон сохранения импульса: 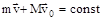 , m и v – масса и скорость пули, M и v0 – масса и скорость ружья. В начальный момент времени (до выстрела) система покоилась (v=v0=0), следовательно константа в уравнении равна нулю. Отсюда, соотношение скоростей v и v0 после выстрела, можно рассчитать из равенства
, m и v – масса и скорость пули, M и v0 – масса и скорость ружья. В начальный момент времени (до выстрела) система покоилась (v=v0=0), следовательно константа в уравнении равна нулю. Отсюда, соотношение скоростей v и v0 после выстрела, можно рассчитать из равенства 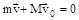 ,
, 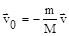 .
.
Т.к. m<<M, то v>>v0; знак «минус» указывает на противоположную направленность скоростей. Эксперименты доказывают, что закон сохранения импульса выполняется и для замкнутых систем микрочастиц, т.е. в квантовой механике. Таким образом, закон сохранения импульса универсален и является фундаментальным законом природы.
2. 4. Центр масс. Закон движения центра масс. @
Центр масс (или центр инерции) системы материальных точек (тел) есть некоторая точка в пространстве С, положение которой характеризует распределение масс системы. Ее радиус-вектор равен : 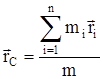 , где n – число точек (тел) системы, m1, m2…mn – их массы;
, где n – число точек (тел) системы, m1, m2…mn – их массы; 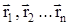 - их радиусы-векторы; m – общая масса системы.Скорость центра масс
- их радиусы-векторы; m – общая масса системы.Скорость центра масс
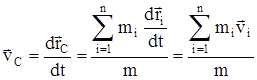 . Так как
. Так как 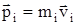 ,
, 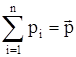 - импульс всей системы, то
- импульс всей системы, то 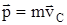 или импульс системы
или импульс системы 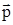 равен произведению массы системы на скорость ее центра масс.
равен произведению массы системы на скорость ее центра масс.
По II закону Ньютона 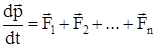 . Отсюда
. Отсюда 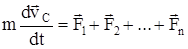 , т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на нее действует сила, равная геометрической сумме всех внешних сил, действующих на тела системы. Это есть закон движения центра масс. Если система замкнута, то
, т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на нее действует сила, равная геометрической сумме всех внешних сил, действующих на тела системы. Это есть закон движения центра масс. Если система замкнута, то 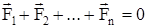 ,
, 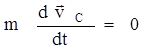 и
и 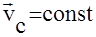 .
.
Следовательно центр масс замкнутой системы движется прямолинейно и равномерно, либо остается неподвижным. Например, молоток вращается, а его центр масс движется прямолинейно и равномерно (рис.2.5).
Рис.2.5. Свободно летящий молоток. Его центр инерции помечен крестиком.
2. 5. Принцип реактивного движения. Уравнение движения тела с переменной массой. @
Особый интерес представляет применение закона сохранения импульса к явлению «непрерывной отдачи», происходящему в реактивном двигателе (ракете). Если рассматривать ракету и выбрасываемые ею продукты сгорания как единую механическую систему, то для получения уравнения ее движения можно применить закон сохранения импульса. Эта идея была высказана в 1881 г. Н.И.Кибальчичем и развита в трудах К.Э.Циолковского. Уравнение движения тела с переменной массой было выведено в 1897г. И.В.Мещерским.
При выводе уравнения необходимо учитывать, что в процессе движения ракеты изменяется ее масса, т.к. удаляются продукты сгорания. Пусть в момент времени t масса ракеты – m и ее скорость - 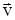 . Через интервал времени dt масса ее уменьшится на dm и станет равной m-dm, а скорость будет равна
. Через интервал времени dt масса ее уменьшится на dm и станет равной m-dm, а скорость будет равна 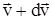 . Образовавшиеся продукты сгорания топлива за время dt приобрели импульс
. Образовавшиеся продукты сгорания топлива за время dt приобрели импульс 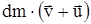 , где
, где 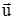 - скорость истечения газа относительно ракеты. Изменение импульса всей системы (ракета + продукты сгорания) за время dt равно
- скорость истечения газа относительно ракеты. Изменение импульса всей системы (ракета + продукты сгорания) за время dt равно
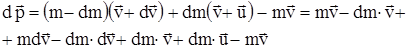
Так как 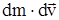 - пренебрежимо малая величина, поэтому после сокращений получим
- пренебрежимо малая величина, поэтому после сокращений получим 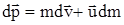 . Полагая, что на ракету в далеком космосе не действуют внешние силы, то из закона сохранения импульса следует, что
. Полагая, что на ракету в далеком космосе не действуют внешние силы, то из закона сохранения импульса следует, что 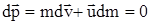 .
.
Разделим обе части равенства на dt и после простых преобразований получим 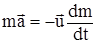 .
.
Выражение в правой части равенства 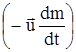 имеет размерность силы и называется реактивной силой
имеет размерность силы и называется реактивной силой 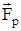 . Таким образом уравнение динамики движения ракеты в космосе можно записать в виде:
. Таким образом уравнение динамики движения ракеты в космосе можно записать в виде: 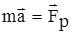 . Интегрируя обе части этого равенства, получим
. Интегрируя обе части этого равенства, получим 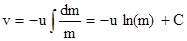 . Постоянную интегрирования С находим из начальных условий : в момент времени t=0 скорость ракеты v=0 и масса m=m0, тогда
. Постоянную интегрирования С находим из начальных условий : в момент времени t=0 скорость ракеты v=0 и масса m=m0, тогда 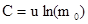 и
и  .
.
Эта формула называется формулой Циолковского. Скорость ракеты v будет тем больше, чем больше масса ракеты и скорость истечения продуктов сгорания топлива.
Если на систему действуют внешние силы 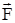 , то
, то 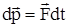 и аналогичным образом плучается уравнение И.В.Мещерского в виде :
и аналогичным образом плучается уравнение И.В.Мещерского в виде : 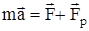
2.6. Энергия, работа, мощность. @
Одного понятия импульса оказалось недостаточно для характеристики движения. Например, два снаряда с массами m1=1кг, m2=10кг и скоростями v1=10м/c, v2=1м/c имеют одинаковые импульс р=10кг×м/с, но их разрушающее действие для преграды будет совершенно разное (у первого в 10 раз больше).
 Единой мерой различных форм движения и взаимодействия всех видов материи является энергия. Различным видам движения и взаимодействия материи, соответствуют различные виды энергии: механическая, тепловая, химическая, электро-магнитная, атомная.
Единой мерой различных форм движения и взаимодействия всех видов материи является энергия. Различным видам движения и взаимодействия материи, соответствуют различные виды энергии: механическая, тепловая, химическая, электро-магнитная, атомная.
Простейшей форме движения – механической, соответствует механическая энергия. Она характеризует способность тела или системы тел совершать работу и измеряется количеством работы, которую при определенных (заданных) условиях может совершить система. Например, катящийся шар, сталкиваясь с некоторым телом, перемещает его, т.е. совершает работу. Растянутая пружина, сокращаясь после устранения деформирующей силы, совершает работу по перемещению своих частей (витков). Следовательно, катящийся шар и растянутая пружина обладают механической энергией.Процесс изменения механической энергии тела под действием силы называется процессом совершения работы. Приращение энергии тела в этом процессе называется работой силы, отсюда следует общее соотношение, связывающее работу и изменение энергии
А=Е2-Е1,
где: А – совершаемая работа, Е1 и Е2 - энергии системы в начальном и конечном состояниях.
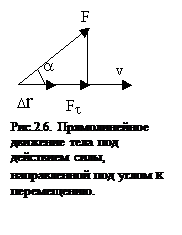
 Сила, приложенная к телу, совершает работу, если тело перемещается.Если тело движется прямолинейно и на него действует постоянная сила, направленная под углом a к перемещению, то работа равна скалярному произведению векторов перемещения и силы (рис.2.6)
Сила, приложенная к телу, совершает работу, если тело перемещается.Если тело движется прямолинейно и на него действует постоянная сила, направленная под углом a к перемещению, то работа равна скалярному произведению векторов перемещения и силы (рис.2.6) 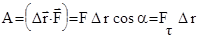 ,где
,где 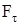 - касательная составляющая силы, т.е. проекция
- касательная составляющая силы, т.е. проекция 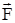 на
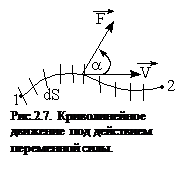
на 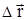 .Если же сила переменна по величине и по направлению или перемещение не прямолинейно, то траекторию движения разбивают на малые участки dS - так, чтобы участок можно было бы считать прямолинейным и силу, действующей на нем - постоянной (рис.2.7). Тогда работа на этом участке
.Если же сила переменна по величине и по направлению или перемещение не прямолинейно, то траекторию движения разбивают на малые участки dS - так, чтобы участок можно было бы считать прямолинейным и силу, действующей на нем - постоянной (рис.2.7). Тогда работа на этом участке 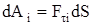 , а работа на всем пути равна сумме всех элементарных работ
, а работа на всем пути равна сумме всех элементарных работ 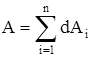 . При
. При 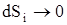
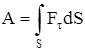 . Для вычисления такого интеграла надо знать зависимость
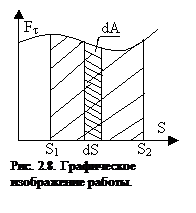
. Для вычисления такого интеграла надо знать зависимость 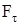 от S. Если эту зависимость представить графически (рис.2.8), тогда работа силы по перемещению из S1 в S2 численно равна площади заштрихованной фигуры, ограниченной кривой F(S), координатной осью S и двумя вертикальными прямыми S1 и S2. Сила не совершает работу (А=0), если Dr=0 или
от S. Если эту зависимость представить графически (рис.2.8), тогда работа силы по перемещению из S1 в S2 численно равна площади заштрихованной фигуры, ограниченной кривой F(S), координатной осью S и двумя вертикальными прямыми S1 и S2. Сила не совершает работу (А=0), если Dr=0 или 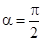 . Если a<
. Если a< 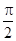 , то А>0; если a>
, то А>0; если a> 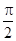 , то А<0. При одновременном действии на тело нескольких сил, работа равна алгебраической сумме работ составляющих сил
, то А<0. При одновременном действии на тело нескольких сил, работа равна алгебраической сумме работ составляющих сил 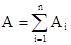 .
.
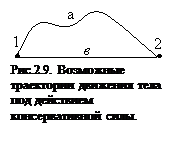
 Сила F называется консервативной, если совершаемая ею работа не зависит от формы траектории, а зависит от начального и конечного положений точки (тела). На рис.2.9. изображены две различные траектории движения тела под действием некоторой консервативной силы. Работа, совершаемая данной силой на пути 1а2 равна А1а2. Работа, совершаемая на пути 2а1, будет отрицательной и А1а2 = - А2а1. Поскольку совершаемая работа не зависит от формы траектории, мы можем записать:
Сила F называется консервативной, если совершаемая ею работа не зависит от формы траектории, а зависит от начального и конечного положений точки (тела). На рис.2.9. изображены две различные траектории движения тела под действием некоторой консервативной силы. Работа, совершаемая данной силой на пути 1а2 равна А1а2. Работа, совершаемая на пути 2а1, будет отрицательной и А1а2 = - А2а1. Поскольку совершаемая работа не зависит от формы траектории, мы можем записать: 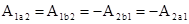 ,
, 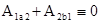 или
или 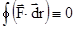 , где
, где 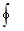 - означает интегрирование вдоль замкнутой траектории или интеграл по контуру. Отсюда следует важное свойство консервативных сил - при перемещении материальной точки (тела) вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Сила всемирного тяготения, сила упругости – консервативные силы. Силы, неудовлетворяющие этому условию называют неконсервативными или диссипативными. Примером таких сил служат силы трения.
- означает интегрирование вдоль замкнутой траектории или интеграл по контуру. Отсюда следует важное свойство консервативных сил - при перемещении материальной точки (тела) вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Сила всемирного тяготения, сила упругости – консервативные силы. Силы, неудовлетворяющие этому условию называют неконсервативными или диссипативными. Примером таких сил служат силы трения.
 Для характеристики скорости совершения работы вводится понятие мощности. Мощностью, развиваемой силой
Для характеристики скорости совершения работы вводится понятие мощности. Мощностью, развиваемой силой 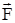 , называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу времени
, называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу времени 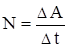 .Если в разные моменты времени dt совершаются разные работы, то используют понятие мгновенной мощности
.Если в разные моменты времени dt совершаются разные работы, то используют понятие мгновенной мощности 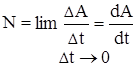 .
.
Для движущихся тел можно получить формулу мгновенной мощности
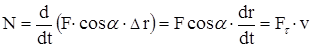 или
или 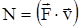 ,
,
т.е. мощность равна скалярному произведению векторов силы и скорости.
Важное требование, предъявляемое к любому двигателю - это способность совершать большую работу за единицу времени, т.е. иметь большую мощность. Из полученной формулы следует, что для достижения этой цели необходимо либо увеличить силу тяги, развиваемую двигателем (например, автомобиля), либо увеличить его быстроходность. Первый путь связан с увеличением силовых нагрузок на все движущиеся части двигателя (поршни, коленчатый вал и т.д.), а они имеют ограниченную прочность. Чтобы детали смогли выдерживать действие больших нагрузок, нужно увеличивать их размеры, делать их более массивными. Поэтому все мощные тихоходные машины необычайно громоздкие. Второй путь позволяет получить большие мощности при малых силовых нагрузках на детали двигателя и меньших его размерах. В современное время этот путь наиболее перспективен.
2.7. Кинетическая и потенциальная энергии. @
Полная механическая энергия Ем складывается из кинетической Ек и потенциальной Еп энергий Ем = Ек + Еп .
Кинетическая энергия Ек – это энергия движущегося тела, она равна работе, которую могло бы совершать тело при торможении до полной остановки Ек=Атор. Соответственно, эта работа численно равна работе внешней силы по увеличению скорости тела от 0 до т.е. Ек=Аразгона.Рассчитаем эту работу, учитывая, что работа внешней силы F над телом на малом участке перемещения dr равна (здесь использован второй закон Ньютона, соотношение 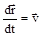 и законы дифференцирования)
и законы дифференцирования)
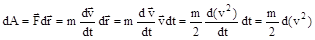 .
.
Так как по определению 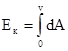 , то получаем
, то получаем 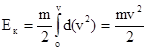 .
.
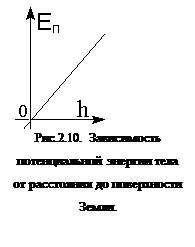 Если система состоит из n движущихся точек (тел), то ее полная кинетическая энергия равна
Если система состоит из n движущихся точек (тел), то ее полная кинетическая энергия равна
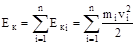 . Если система обладает только кинетической энергией, то изменение кинетической энергии тела равно работе сил, действовавших на тело во время движения
. Если система обладает только кинетической энергией, то изменение кинетической энергии тела равно работе сил, действовавших на тело во время движения 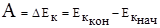 .
.
Потенциальная энергия Еп – это энергия взаимодействия тел системы, определяемая взаимным расположением тел и характером сил взаимодействия между ними. Потенциальная энергия - величина, зависящая от выбора начального положения, при котором Еп=0, т.е. она величина относительная. Если работу совершают консервативные силы, то происходит изменение Еп системы на величину 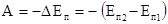 . Конкретный вид зависимости Еп от расположения тел системы связан с характером сил взаимодействия тел.
. Конкретный вид зависимости Еп от расположения тел системы связан с характером сил взаимодействия тел.
Рассмотрим два примера:
 1). Определим Еп тела, поднятого над землей т.е. энергию взаимодействия этого тела с планетой Земля. Известно, что на тело действует консервативная сила тяжести, при небольших высотах h она мало меняется и считается по формуле P = mg. При падении тела сила тяжести совершает работу A=mgh, при этом потенциальная энергия тела уменьшается ровно на эту величину. Если Еп1- потенциальная энергия тела, поднятого над землей, а Еп2 - потенциальная энергия тела на поверхности земли, которую принято считать равной нулю, то из связи работы и изменения энергии, получим
1). Определим Еп тела, поднятого над землей т.е. энергию взаимодействия этого тела с планетой Земля. Известно, что на тело действует консервативная сила тяжести, при небольших высотах h она мало меняется и считается по формуле P = mg. При падении тела сила тяжести совершает работу A=mgh, при этом потенциальная энергия тела уменьшается ровно на эту величину. Если Еп1- потенциальная энергия тела, поднятого над землей, а Еп2 - потенциальная энергия тела на поверхности земли, которую принято считать равной нулю, то из связи работы и изменения энергии, получим 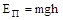 . График зависимости Еп от h представлен на рис.2.10. Ясно, что Еп1>0 при h>0, т.е. над землей и Еп2<0 при h<0, т.е. ниже уровня земли.
. График зависимости Еп от h представлен на рис.2.10. Ясно, что Еп1>0 при h>0, т.е. над землей и Еп2<0 при h<0, т.е. ниже уровня земли.
2). Определим потенциальную энергию упруго деформированной пружины. Из экспериментов известно, что при сжатии (растяжении) пружины в ней возникает сила упругости 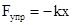 . Знак минус показывает, что сила упругости направлена в сторону противоположную деформации. Работа этой силы затрачивается на увеличение потенциальной энергии пружины т.е. A=DEп= Еп2- Еп1 . Так как dA=Fdx=kxdx, то
. Знак минус показывает, что сила упругости направлена в сторону противоположную деформации. Работа этой силы затрачивается на увеличение потенциальной энергии пружины т.е. A=DEп= Еп2- Еп1 . Так как dA=Fdx=kxdx, то 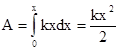 (Еп недеформированной пружины считается равной нулю). Следовательно
(Еп недеформированной пружины считается равной нулю). Следовательно 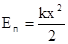 , на рис.2.11 представлен ее график.
, на рис.2.11 представлен ее график.
2.8. Связь потенциальной энергии тела и действующей на него консервативной силы. @
Так как работа консервативной силы равна убыли потенциальной энергии, то 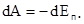 или
или 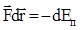 . Высшая математика позволяет выразить малое изменение любой функции (дифференциал функции) через частные производные от этой функции по ее аргументам. Конкретно для дифференциала потенциальной энергии, зависящей от координат, можно получить
. Высшая математика позволяет выразить малое изменение любой функции (дифференциал функции) через частные производные от этой функции по ее аргументам. Конкретно для дифференциала потенциальной энергии, зависящей от координат, можно получить 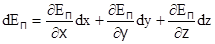 . Если подставить это выражение в
. Если подставить это выражение в 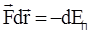 , то после записи левой части через проекции силы на оси координат, получим
, то после записи левой части через проекции силы на оси координат, получим
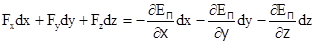 .
.
Это выражение должно быть справедливо при любых малых перемещениях dx, dy, dz, что может быть только тогда, когда выполняются соотношения 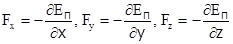 .
.
В результате получаем связь между Еп и F, в векторной форме ее записывают сокращенно в виде
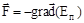 ,
,
где используют математический символ для вектора, который называется градиентом скалярной величины Еп и обозначается grad (Еп) 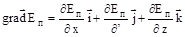 .
.
2.9. Закон сохранения и превращения энергии в механике. @
В 1748 г. М.В.Ломоносов сформулировал закон сохранения материи и движения. Через 100 лет Р.Майер и Г.Гельмгольц дали количественную формулировку закона сохранения и превращения энергии.
В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела другому, но общее количество энергии остается неизменным. В природе и технике постоянно имеют место превращения одних видов энергии в другие. Например, в электродвигателях электрическая энергия переходит в механическую, в ядерном реакторе ядерная энергия переходит в тепловую, затем в механическую и электромагнитную, при фотоэффекте - электромагнитная в электрическую и т.д. Однако следует иметь в виду, что одновременно может происходить несколько типов превращений энергии, например, обычно некоторая часть энергии непременно превращается во внутреннюю (тепловую) энергию вещества (в энергию теплового движения молекул). Но всегда общий запас энергии системы в любой момент времени остается неизменным. Закон сохранения и взаимопревращения энергии является всеобщим законом природы, не имеющим исключений; если он как бы нарушается в эксперименте, значит что-то не учтено.
Закон сохранения механической энергии формулируется следующим образом: Если в замкнутой системе действуют консервативные силы, то механическая энергия не переходит в другие виды и остается постоянной во времени (при этом возможен переход потенциальной энергии в кинетическую и наоборот) 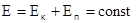 .
.
Продемонстрируем действие этого закона на примере свободного падения тела.
 Пример: Пусть тело массой m начинает падать вниз с высоты h.
Пример: Пусть тело массой m начинает падать вниз с высоты h.
Рассчитаем его механическую энергию в различные моменты времени. В начальный момент времени, в верхней точке его механическая энергия равна mgh (Ек =0 так как начальная скорость равна нулю).
Если не учитывать силы трения о воздух, то в любой следующий момент времени t координату и скорость тела можно рассчитать с помощью законов кинематики для равноускоренного движения с ускорением свободного падения g (см. рис.2.12): z = h ‑ gt2/2, v = ‑ gt.
Механическая энергия в этот момент времени будет равна
Ем = Еп + Ек = mgz + mv2/2 = mg(h – gt2/2) + m(gt)2/2 = mgh, т.е. равна энергии в начальный момент времени. Отсюда видно, что механическая энергия не меняется со временем. Если же рассматривать и действие сил трения, то окажется, что механическая энергия тела при движении уменьшается. Это объясняется частичным превращением ее во внутреннюю (тепловую) энергию воздуха и самого тела.
3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. @
3.1. Основные характеристики динамики вращательного движения. @
Для описания вращательного движения используются следующие параметры : момент инерции J, момент силы 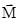 , момент импульса тела
, момент импульса тела 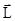 . Аналогами их в поступательном движении являются масса m, сила
. Аналогами их в поступательном движении являются масса m, сила 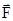 , импульс тела
, импульс тела 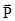 .
.
Момент инерции материальной точки относительно некоторой оси есть скалярная физическая величина равная произведению массы этой точки на квадрат кратчайшего расстояния от нее до оси вращения 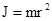 .
.
 Чтобы рассчитать момент инерции твердого тела, его мысленно разбивают на n материальных точек с массами Dm1, Dm2,..., Dmn, находящихся на расстояниях r1, r2,..., rn от оси вращения. Момент инерции твердого тела J, вращающегося вокруг неподвижной оси равен алгебраической сумме моментов инерции всех точек, из которых состоит тело
Чтобы рассчитать момент инерции твердого тела, его мысленно разбивают на n материальных точек с массами Dm1, Dm2,..., Dmn, находящихся на расстояниях r1, r2,..., rn от оси вращения. Момент инерции твердого тела J, вращающегося вокруг неподвижной оси равен алгебраической сумме моментов инерции всех точек, из которых состоит тело 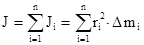 . При непрерывном распределении масс тела эта сумма сводится к интегралу
. При непрерывном распределении масс тела эта сумма сводится к интегралу 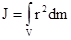 , где V - объем тела, r – кратчайшее расстояние от точки до оси вращения. На основании этой формулы рассчитываются моменты инерции тел различной формы. Например: 1) полый тонкостенный цилиндр или обруч радиуса R, массой m и осью вращения, совпадающей с осью симметрии
, где V - объем тела, r – кратчайшее расстояние от точки до оси вращения. На основании этой формулы рассчитываются моменты инерции тел различной формы. Например: 1) полый тонкостенный цилиндр или обруч радиуса R, массой m и осью вращения, совпадающей с осью симметрии 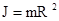 ; 2) сплошной цилиндр или диск радиуса R, массой m и осью вращения, совпадающей с осью симметрии
; 2) сплошной цилиндр или диск радиуса R, массой m и осью вращения, совпадающей с осью симметрии 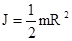 ; 3) шар радиуса R, массой m и осью вращения, проходящей через его центр
; 3) шар радиуса R, массой m и осью вращения, проходящей через его центр 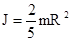 . Приведенные примеры показывают, что момент инерции тела зависит от его массы, формы, геометрических размеров, его расположения относительно оси вращения, распределения массы по объему тела.
. Приведенные примеры показывают, что момент инерции тела зависит от его массы, формы, геометрических размеров, его расположения относительно оси вращения, распределения массы по объему тела.
Расчет моментов инерции тел относительно осей, не совпадающих с осью симметрии более сложен. В таких случаях применяется теорема Штейнера: момент инерции любого тела относительно произвольной оси ОО¢ равен сумме момента инерции этого тела JO относительно оси АА¢ , параллельной данной и проходящей через центр масс тела С, и произведения массы тела на квадрат расстояния между осями (рис.3.1) 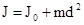 .
.
Моментом силы 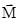 относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора
относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора 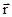 , проведенного из точки О в точку приложения силы, на вектор силы:
, проведенного из точки О в точку приложения силы, на вектор силы: 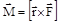 .
.
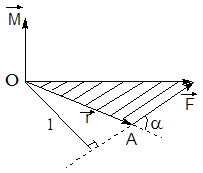 Рис.3.2. Момент силы относительно неподвижной точки.
Рис.3.2. Момент силы относительно неподвижной точки.
|
Направление 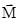 перпендикулярно плоскости, в которой лежат вектора
перпендикулярно плоскости, в которой лежат вектора 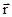 и
и 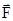 . Его направление совпадает с направлением поступательного движения правого винта при его вращении от
. Его направление совпадает с направлением поступательного движения правого винта при его вращении от 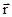 к
к 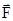 (рис.3.2). Модуль момента силы
(рис.3.2). Модуль момента силы
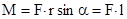 ,
, 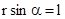 - плечо силы - кратчайшее расстояние между линией действия силы и точкой О. Если к точке А приложено несколько сил, то результирующий
- плечо силы - кратчайшее расстояние между линией действия силы и точкой О. Если к точке А приложено несколько сил, то результирующий 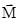 будет равен векторной сумме моментов слагаемых сил:
будет равен векторной сумме моментов слагаемых сил:
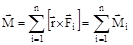
Момент силы, действующей на тело относительно неподвижной оси z, есть скалярная величина Mz, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки О данной оси z (рис.3.3) 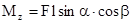 .
.
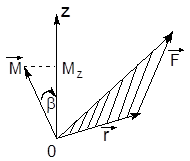 Рис.3.3. Момент силы относительно неподвижной оси.
Рис.3.3. Момент силы относительно неподвижной оси.
|
Значение момента Mz не зависит от положения точки О на оси z. Если ось z совпадает с направлением вектора 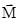 , то момент силы равен
, то момент силы равен 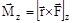 .
.
Момент импульса (количества движения) материальной точки А относительно неподвижной точки О есть векторная физическая величина, определяемая векторным произведением двух векторов: радиуса-вектора 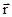 , проведенного из точки О в точку А, и импульса материальной точки
, проведенного из точки О в точку А, и импульса материальной точки 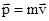
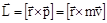 .
.
Направление вектора 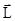 совпадает с направлением поступательного движения правого винта при его вращении от
совпадает с направлением поступательного движения правого винта при его вращении от 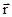 к
к 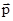 (рис.3.4).
(рис.3.4).
 Рис.3.4. Момент импульса относительно неподвижной точки.
Рис.3.4. Момент импульса относительно неподвижной точки.
|
Модуль вектора 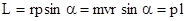 , a - угол между векторами
, a - угол между векторами 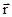 и
и 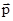 , l - плечо вектора
, l - плечо вектора 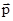 (или
(или 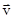 ) относительно точки О.
) относительно точки О.
Моментом импульса точки относительно неподвижной оси z называется скалярная величина Lz равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси 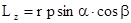 , где
, где 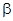 угол между вектором
угол между вектором 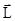 и осью z.
и осью z.
Момент импульса твердого тела есть векторная сумма моментов импульса всех точек, из которых состоит тело. Если число точек системы равно n, тогда 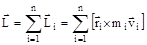 .
.
При вращательном движении твердого тела вокруг неподвижной оси угловые скорости w всех его точек равны, угол между векторами 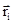 и
и 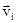 равен
равен 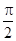 и все вектора
и все вектора 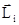 направлены по оси вращения в одну сторону. Отсюда модуль вектора
направлены по оси вращения в одну сторону. Отсюда модуль вектора 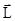 тела равен
тела равен 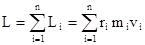 ,
, 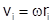 ,
,
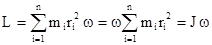 .
.
Момент импульса твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции этого тела относительно той же оси на угловую скорость.Направления векторов 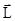 и
и 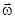 совпадают и
совпадают и 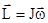 .
.
3. 2. Работа и кинетическая энергия при вращательном движении твердого тела. @
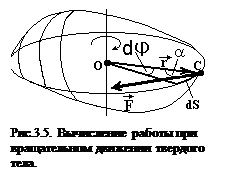
Найдем работу при вращательном движении твердого тела. Пусть ось вращения проходит через точку О, находящуюся на расстоянии r от точки приложения силы С, а a ‑ угол между векторами 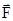 и
и 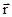 (рис.3.5). При повороте тела на бесконечно малый угол dj точка приложения силы проходит путь dS=rdj. Работа силы равна произведению проекции силы вдоль смещения Fsin(a) на величину этого смещения r dj .
(рис.3.5). При повороте тела на бесконечно малый угол dj точка приложения силы проходит путь dS=rdj. Работа силы равна произведению проекции силы вдоль смещения Fsin(a) на величину этого смещения r dj . 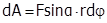 . Но F×r×sin(a ) = M - момент силы. Таким образом: работа силы при вращении тела вокруг неподвижной оси равна произведению момента действующей силы на угол поворота dA = Mdj.
. Но F×r×sin(a ) = M - момент силы. Таким образом: работа силы при вращении тела вокруг неподвижной оси равна произведению момента действующей силы на угол поворота dA = Mdj.
 Чтобы рассчитать кинетическую энергию вращательного движения твердого тела, мысленно его разобьем на n материальных точек с массами m1, m2,...,mn, находящихся на расстояниях r1, r2,...,rn от оси вращения. Так как тело абсолютно твердое, угловые скорости всех его точек одинаковы
Чтобы рассчитать кинетическую энергию вращательного движения твердого тела, мысленно его разобьем на n материальных точек с массами m1, m2,...,mn, находящихся на расстояниях r1, r2,...,rn от оси вращения. Так как тело абсолютно твердое, угловые скорости всех его точек одинаковы
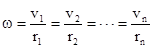 .
.
Линейные скорости точек будут разные 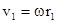 ,
, 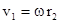 и т.д. Кинетическая энергия вращающегося тела Ек.вр равна
и т.д. Кинетическая энергия вращающегося тела Ек.вр равна
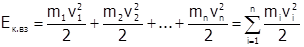 ;
;
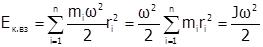 .
.
Работа внешних сил при вращении тела идет на увеличение его кинетической энергии. dA=dЕк.вр, следовательно работу можно представить как разность кинетических энергий конечного и начального положений
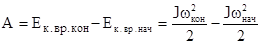
Если тело катится без скольжения, то оно одновременно участвует в двух движениях : поступательном и вращательном, и его кинетическая энергия
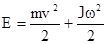 .
.
3. 3. Основное уравнение вращательного движения тела вокруг неподвижной оси. @
Воспользуемся соотношением, приведенным выше dA=dEвр, т.е.
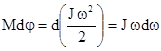
Поделим обе части равенства на dt:
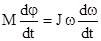 и так как
и так как 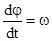 , а
, а 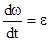 , то
, то 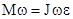 или
или 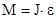
В векторном вид 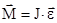 или
или 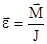 представляет собой уравнение динамики вращательного движения твердого тела вокруг неподвижной оси, проходящей через центр масс тела. Угловое ускорение, приобретаемое телом при вращении его вокруг неподвижной оси, прямо пропорционально вращающему моменту сил и обратно пропорционально моменту инерции тела. По форме оно сходно с уравнением II закона Ньютона. Из их сопоставления вытекает, что при вращательном движении роль массы играет момент инерции, роль линейного ускорения - угловое ускорение, роль силы - момент силы.
представляет собой уравнение динамики вращательного движения твердого тела вокруг неподвижной оси, проходящей через центр масс тела. Угловое ускорение, приобретаемое телом при вращении его вокруг неподвижной оси, прямо пропорционально вращающему моменту сил и обратно пропорционально моменту инерции тела. По форме оно сходно с уравнением II закона Ньютона. Из их сопоставления вытекает, что при вращательном движении роль массы играет момент инерции, роль линейного ускорения - угловое ускорение, роль силы - момент силы.
Ранее получено, что 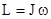 . Возьмем первую производную по времени от этого равенства
. Возьмем первую производную по времени от этого равенства
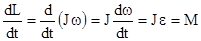 .
.
Это выражение есть вторая (более общая) форма уравнения динамики вращательного движения твердого тела: Скорость изменения момента импульса тела равна результирующему моменту всех внешних сил, 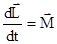 (оно сходно с законом динамики поступательного движения:
(оно сходно с законом динамики поступательного движения: 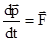 ).
).
Если на тело не действуют внешние силы или система тел замкнутая, то момент сил 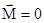 и
и 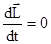 , откуда
, откуда 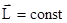 и получаем закон сохранения момента импульса: Момент импульса замкнутой системы тел остается постоянным во времени. Аналогом его в поступательном движении является закон сохранения импульса замкнутой системы тел. Закон сохранения момента импульса справедлив и для тел, размеры, форма и момент инерции которых могут меняться в ходе движения. Поскольку величина
и получаем закон сохранения момента импульса: Момент импульса замкнутой системы тел остается постоянным во времени. Аналогом его в поступательном движении является закон сохранения импульса замкнутой системы тел. Закон сохранения момента импульса справедлив и для тел, размеры, форма и момент инерции которых могут меняться в ходе движения. Поскольку величина 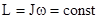 , то при увеличении момента инерции J, угловая скорость w уменьшается и наоборот. К примеру, акробат, совершая переворот в воздухе, чтобы увеличить угловую скорость своего вращения, группируется, т.е. прижимает к себе руки и ноги. При этом его момент инерции уменьшается.
, то при увеличении момента инерции J, угловая скорость w уменьшается и наоборот. К примеру, акробат, совершая переворот в воздухе, чтобы увеличить угловую скорость своего вращения, группируется, т.е. прижимает к себе руки и ноги. При этом его момент инерции уменьшается.
4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ. @
4.1. Основные характеристики гармонического колебания. @
Колебательным движением называется процесс, при котором система многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Промежуток времени Т, спустя который процесс полностью повторяется, называется периодом колебания.
Колебательные движения широко распространены в природе и технике. Качание маятника часов, вибрация натянутой струны, морские приливы-отливы, тепловые колебания ионов кристаллической решетки твердого тела, переменный электрический ток, свет, звук. В зависимости от характера воздействия на колеблющуюся систему различают свободные незатухающие (или собственные) колебания, затухающие колебания, вынужденные колебания, автоколебания.
Свободные колебания происходят в системе, предоставленной самой себе после того, как она была выведена из положения равновесия. Простейшим свободным периодическим механическим колебанием является гармоническое колебательное движение точки (тела), при котором зависимость смещения из положения равновесия S от времени t описывается уравнениями:
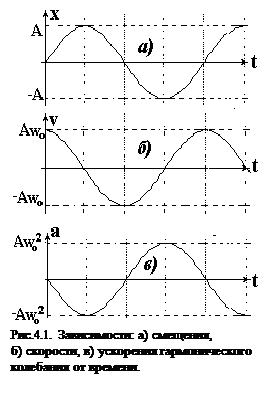
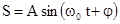 или
или 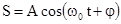 ,
,
А - амплитуда колебаний или максимальное смещение из положения равновесия, w0 - круговая (циклическая) частота, 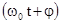 - фаза колебаний в момент времени t, j - начальная фаза колебаний или фаза в момент времени t=0. Такие колебания происходят под действием так называемых квазиупругих сил. Квазиупругие силы - это силы, имеющие такую же закономерность, как и сила упругости.
- фаза колебаний в момент времени t, j - начальная фаза колебаний или фаза в момент времени t=0. Такие колебания происходят под действием так называемых квазиупругих сил. Квазиупругие силы - это силы, имеющие такую же закономерность, как и сила упругости.
Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер близкий к гармоническим; 2) различные периодические процессы можно представить как сложение нескольких гармонических колебаний.
Через время Т фаза колебания получит приращение 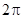 и колебательный процесс повторяется:
и колебательный процесс повторяется: 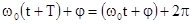 , откуда
, откуда 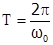 . Число полных колебаний в единицу времени есть частота колебаний n, для нее вытекают соотношения
. Число полных колебаний в единицу времени есть частота колебаний n, для нее вытекают соотношения 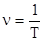 ,
, 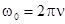 .Так как значения синуса и косинуса изменяются в пределах от +1 до -1, S принимает значения от +А до -А.
.Так как значения синуса и косинуса изменяются в пределах от +1 до -1, S принимает значения от +А до -А.
4.2. Скорость и ускорение при гармоническом колебании. @
Скорость гармонического колебания есть первая производная от смещения S по времени t. Пусть 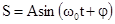 , тогда
, тогда
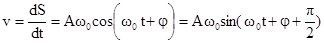 . Скорость сдвинута по фазе относительно смещения
. Скорость сдвинута по фазе относительно смещения
Дата добавления: 2022-05-27; просмотров: 59;










