Семантика исчисления предикатов

Для уяснения смысла аксиом и правил вывода введем понятие интерпретации языка и исчисления α.

Определение 9.25. Под интерпретацией языка исчисления α понимают любое множество М с зафиксированным отображением u сигнатуры σ во множество операций и предикатов, определенных на М, при котором символу n-арной операции f из σ соответствует n-арная операция f^u, определенная на множестве М, а символу n-арного предиката р из σ n-арный предикат р^u на М. Образ множества σ при отображении u обозначим через σ^u. В частности, образом констант из σ при u будут нуль-арные операции на М, т. е. некоторые элементы из М.

Если (М, u) — интерпретация языка α, то, заменив в любой формуле языка α константы, символы операций и символы предикатов их образами при u и условившись переменным из Х придавать значения из множества М, мы получим формулу А^u алгебры предикатов на алгебраической системе М(σ^u), и можно говорить о выполнимости, истинности или ложности этой формулы на системе М(σ^u).

Определение 9.26. Формула А исчисления предикатов называется выполнимой, истинной, ложной в интерпретации (М, u), если соответственно выполнима, истинна, ложна формула А^u на алгебраической системе М(σ^u).

Определение 9.27. Формула А исчисления предикатов α называется тождественно истинной, если она истинна во всех интерпретациях исчисления α.

Естественно возникает вопрос о соотношении между классами доказуемых и истинных формул исчисления предикатов. Ответ на этот вопрос можно получить из следующих теорем.

Теорема 9.28. Если каждая формула множества формул Т истинна в некоторой интерпретации (М, u) исчисления α и T├─ A, то А — истинна в (М, u).

Доказательство. Для простоты записей условимся считать, что операции и предикаты на М обозначены теми же буквами, что и соответствующие им символы операций из σ. Тогда u — тождественное отображение и в записи А^u индекс u можно опускать.

Из определения доказуемой формулы следует, что достаточно доказать два утверждения:

а) все аксиомы истинны;

б) формула, являющаяся непосредственным следствием по любому правилу вывода из истинных формул, является истинной.

Истинность аксиом первых четырех групп аксиом доказывается одним методом. Проиллюстрируем его на аксиоме I₁: A ® (B ® A).

Заменив в А, В свободные вхождения переменных элементами из М, получим высказывания, имеющие вполне определенные значения £ и ß (каждое из £, ß есть «и» или «л»). Перебирая всевозможные наборы значений «и» и «л» для £, ß мы непосредственной проверкой (пользуясь определением операции ®) убедимся в том, что при любых £, ß £ ® (ß ® £) º и.

Отсюда следует, что аксиома I₁ истинна в интерпретации (М, u).

Докажем теперь истинность аксиомы

V₁ : "x A(x) ® A(t),

где t — терм, свободный для х в А(х). Пусть х, х₁, …, х_n суть все переменные, имеющие свободные вхождения в А(х) и x_i1, …, x_im — все переменные, участвующие в образовании терма t. Так как t свободен для х в А(х), то все вхождения переменных x_i1, …, x_im в терм t останутся свободными при подстановке t вместо х в формулу А(х). В связи с этим запишем:

A(t) = A(t(x_i1, …, x_im), х₁, …, х_n).

Допустим, что формула V₁ не истинна в интерпретации (М, u). Это означает, что при некотором наборе значений переменных х₁ = a₁, …, х_n = a_n, x_i1 = a_i1, …, x_im = a_im формула "x A(x) принимает значение «и», а формула A(t) — значение «л». Если обозначить через b значение терма t при x_i1 = a_i1, …, x_im = a_im, то будем иметь: с одной стороны, A(х₀, a₁, …, a_n) является истинным высказыванием при любом значении х₀ Î М, а с другой стороны, высказывание A(b, a₁, …, a_n) — ложно. Полученное противоречие и доказывает наше утверждение.

Аналогично доказывается, что правила вывода позволяют из истинных формул в интерпретации (М, u) получать снова истинные формулы, т.е.:

1) если истинны формулы А и А ® В, то истинна и формула В;

2) если истинна формула В ® А(х) и х не имеет свободных вхождений в В, то истинна формула В ® "х А(х);

3) если истинна формула А(х) ® В и х не имеет свободных вхождений в В, то истинна и формула $х А(х) ® В.

Теорема доказана.

Следствие 9.29. Всякая доказуемая формула исчисления предикатов α является истинной в любой интерпретации (М, u) исчисления α.

Замечание. Теорема и следствие теряют силу, если в аксиомах V₁ и V₂ не накладывать ограничений на терм t или в правилах "-введения и $-удаления разрешить свободные вхождения х в В. Приведем соответствующие примеры.

1. Пусть множество натуральных чисел N, A(x) = $y (x < y) и t = x + y — терм, не свободный для х в А(х), поскольку свободное вхождение буквы х в А(х) находится в области действия квантора $ по букве у, входящий в терм t. Нетрудно видеть, что формула "x A(x) ® A(t), или подробнее, "x($y(x < y)) ® $y(x + y < y) ложна в арифметике.

2. В той же интерпретации, положим B = (x £ y), A = (x £ y + 1). Тогда имеем: формула В ® А истинна на N, а формула В ® "xА ложна, поскольку, например, при х = 2, у = 3 имеем (2 £ 3) º и, "x (x £ 4) º л.

Доказанная теорема свидетельствует о том, что логические средства исчисления предикатов выбраны разумно, поскольку с их помощью можно доказать только утверждения, истинные с содержательной точки зрения.

Следствие 9.30. Исчисление предикатов непротиворечиво, т.е. в нем не может быть доказуемой никакая формула А вместе с ее отрицанием, или никакая формула вида .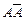

Действительно формула 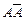является ложной в любой интерпретации, тогда как доказуемые формулы истинны в любой интерпретации.

Теперь естественно возникает вопрос: не слишком ли мало аксиом и правил вывода мы взяли при построении исчисления предикатов? Так, из доказательства предыдущей теоремы видно, что если бы нашлась формула А, не доказуемая в исчислении предикатов, но истинная в любой его интерпретации, то, присоединив А к системам аксиом, мы получили бы более сильное и непротиворечивое логическое исчисление. Однако ниже будет показано, что такой формулы А не существует, а именно имеет место следующая теорема Геделя о полноте исчисления предикатов.

Теорема 9.31. Если формула исчисления предикатов истинна во всех его интерпретациях, то она доказуема в исчислении предикатов.

Для доказательства этой теоремы введем сначала некоторые понятия и докажем одно общее утверждение (см. теорему 9.7.11).

Определение 9.32. Множество формул Т исчисления α называется противоречивым, если существует такая формула А языка α, что Т├─ 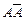. В противном случае Т называется непротиворечивым.

Определение 9.33. Множество формул Т исчисления α называется выполнимым, если существует интерпретация, в которой все формулы из Т принимают истинное значение хотя бы при одной (общей для всех формул из Т) замене переменных.

Определение 9.34. Множество формул Т исчисления α называется полным, если для каждой замкнутой формулы языка α имеет место Т├─ А или Т ├─ .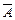

Теорема 9.35. Всякое непротиворечивое множество S замкнутых формул исчисления α выполнимо.

Доказательство. Добавим к множеству символов языка α еще счетное множество констант (символов нуль-арных операций) ß = {b₀, b₁, b₂, …}.

Получим новый язык α₁ в сигнатуре σ₁ = σ È ß. Заменяя в аксиомах и правилах вывода исчисления α формулы языка α₁, мы получим новое логическое исчисление, которое обозначим той же буквой α₁. Из определения языка α₁ видно, что все доказанные факты об исчислении α (в частности, все доказанные формулы и дополнительные правила вывода) сохраняются и в α₁. Так как язык α₁ включает в себя α, то S можно рассматривать как множество предложений языка α₁. Легко видеть, что S будет непротиворечивым и в исчислении α₁. Действительно, если в α₁ из S выводима формула 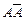, то, заменив в формулах вывода 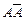из S все константы из ß переменными, не участвующими в этом выводе, мы получим вывод в α из S формулы 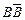, где В получается из А указанной заменой констант. Чтобы убедиться в этом, достаточно заметить, что указанная замена аксиомы переводит в аксиомы и сохраняет свойство формулы быть непосредственным следствием предыдущих формул. Таким образом, S непротиворечиво в α₁.

Теперь расширим определенным образом множество S. Для этого занумеруем все замкнутые формулы исчисления α₁: А₀, А₁, А₂, …

По формуле А₀ и системе S построим множество формул S₀, положив:

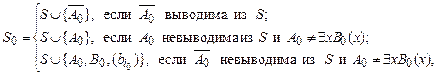где b_i0 — символ с наименьшим номером из ß, не встречающийся в А₀. Из определения S₀ имеем: S Î S₀ и S₀ ├─ А₀ или S₀ ├─ .

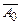Покажем, что S₀ непротиворечиво. Допустим, что в α₁ S₀ ├─ 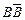. В соответствии с определением S₀ рассмотрим три случая.

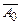1. S ├─ `А<sub>0</sub>. Тогда S<sub>0</sub> = S È { } и из (9.5) имеем: S, `А₀ ├─ 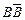. Отсюда по следствию из теоремы дедукции получаем S ├─ 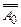, что невозможно в силу непротиворечивости S.

2. 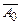невыводима из S и А₀ не имеет вида $х В₀(х). Тогда S₀ = S È {А₀} и мы точно так же, как и в случае «а», получим S ├─ 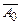, что противоречит условию.

3. 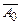невыводима из S и А₀ = $х В₀(х). Тогда S₀ = = S È {А₀, B₀, (b_i0)}, и потому S, А₀, B₀, (b_i0) ├─ 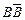. Так как формула B₀ (b_i0) замкнута, то тем же приемом, что и выше, получим S, А₀ ├─ 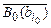. Так как b_i0 не входит в А₀ и в формулы из S, то, повторив весь вывод с заменой b_i0 на переменную x_J, не входящую в участвующие в выводе формулы, мы получим S, А₀ ├─ 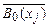, или S ├─ А₀ ® 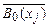. Дополним вывод А₀ ® 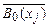из S формулами:

А0 ® "xj	(правило "-введения)
"xj ®	(аксиома)
А0 ®	(правило силлогизма)
А0 ® "x	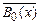(правило "-введения)
"x 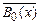®	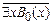(правило $-отрицания)
А0 ®	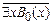(правило силлогизма)

Поскольку $xB₀(x) = А₀, то мы получили вывод из S формулы А₀ ® 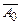, т.е. S, А₀├─ `А₀. А так как S, А₀ ├─ А₀, то по правилу умножения формул S, А₀├─ А₀ 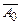. Отсюда следует: S├─ А₀, и мы снова пришли к противоречию с условием. Тем самым мы закончили доказывать непротиворечивость множества формул S₀.

Далее, по А₁ и S₀ мы аналогично построим непротиворечивое множество S₁ такое, что: S₀ Ì S₁, S₁├─ А₁ или S₁├─ .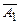

Продолжая этот процесс, мы получим последовательность непротиворечивых множеств формул S₀ Ì S₁ Ì S₂ Ì … таких, что S_i├─ А_i и S_i├─ 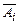. Следовательно, 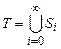есть непротиворечивое и полное множество формул.

Теперь построим интерпретацию исчисления предикатов α, в которой истинны все формулы из α. В качестве основного множества возьмем множество М термов языка α₁, в которых нет предметных переменных — это так называемые замкнутые термы языка α₁. Определим на М операции f^u и предикаты р^u, соответствующие символам операций f и предикатов р из α.

Если а — символ 0-арной операции из σ, то положим а^u = а. Если f — символ n-арной операции из σ, p — символ n-арного предиката и t₁, …, t_n — термы из М, то положим f^u (t₁, …, t_n) = f(t₁, …, t_n):

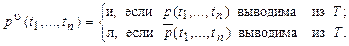
Тем самым определена интерпретация (М, σ) исчисления α₁, а потому и α.

Теперь индукцией по рангу формулы А докажем, что для любой замкнутой формулы языка α₁:

Т├─ А в α₁ Û А^u º и в (М, σ). (9.7)

Для упрощения записи верхний индекс u у формул будем опускать. Если А = р(t₁, …, t_n) — элементарная формула, то (9.7) верно по определению предиката р.

Пусть А — замкнутая формула ранга r > 0. В зависимости от последней операции в А возможны шесть случаев.

1. А = А₁А₂. Используя определение конъюнкции, предположение индукции и правила умножения и разделения формул, получим: А º и Û А₁ = и, А₂ = и Û Т├─ А₁, Т├─ А₂ Û Т├─ А₁А₂.

2. А = А₁ Ú А₂. Если А₁ Ú А₂ º и, то А₁ = и или А₂ = и. Тогда по предположению индукции Т├─ А₁ или Т├─ А₂, а поэтому и Т├─ А₁ Ú А₂. Обратно, пусть Т├─ А₁ Ú А₂. Если Т├─ А₁ или Т├─ А₂, то по предположению индукции А₁ º и или А₂ º и, а потому и А º и. В противном случае, в силу полноты системы Т имеем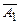: Т├─ , Т├─ 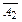. Тогда по правилам умножения формул и де Моргана получим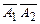: Т├─ ` , Т├─ 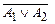. Итак, имеем: Т├─ А₁ Ú А₂, Т├─ 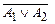, что невозможно в силу непротиворечивости Т.

3. А =`А<sub>1</sub>. Учитывая предположение индукции и полноту системы формул Т, получим: А º и Û А º л Û Т├─ `А₁ Û Т├─ А.

4. А = А₁ ® А₂. В этом случае, используя предположение индукции и правила введения посылки, контрапозиции и двойного отрицания, получим: А º и Û А₁ º л или А₂ º и Û Т├─ `А<sub>1</sub>, или Т├─ `А₂ Û Т├─ `А<sub>2</sub> ®`А₁ или Т├─ А₂ ® А₁ Û Т├─ А.

5. А = "хА₁(х). Если А º и, то А₁(t) º и при любом t Î M. Тогда по предположению индукции Т├─ А₁(t) для всех t Î M. Допустим, что T ├─ 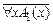. Тогда по правилу "-отрицания T ├─ 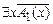и по построению множества Т в Т существует формула 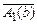при некоторой константе b Î M. В итоге мы получили: Т├─ А₁(t) при любом t Î M и Т├─ А₁(b) при b Î M, что невозможно в силу непротиворечивости Т. Следовательно, T ├─ "хА₁(х). Обратно, пусть T ├─ "хА₁(х). Если "хА₁(х) ¹ и, то А₁(t) º л при некотором t Î M. Тогда по предположению индукции Т├─ 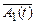. Отсюда по аксиоме V₂ и по правилу "-отрицания получим T ├─ 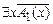и T ├─ 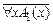, что невозможно в силу непротиворечивости Т.

6. А = $хА₁(х). Если А º и, то А₁(t) º и при некотором t Î M и по предположению индукции Т├─ А₁(t). Отсюда, используя аксиому V₂, получим T ├─ $хА₁(х), т.е. Т├─ А. Обратно, если Т├─ А, то в силу непротиворечивости Т получим, что 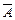не выводима из Т. Тогда, по построению Т, в Т содержится формула А₁(b) при некотором b Î M. По предположению индукции А₁(b) º и, а потому и $хА₁(х) = и.

Таким образом, все замкнутые формулы языка α, выводимые из Т, истинны в интерпретации (М, u). А так как S Ì T, то и все формулы из S истинны в (М, u), т.е. множество S выполнимо и теорема доказана.

Теперь можно доказать и теорему Гёделя о полноте исчисления α. Пусть А — формула исчисления предикатов α и А º и в любой интерпретации исчисления α. Если х₁, …, х_n суть все переменные, имеющие свободные вождения в А, то формула В = "х₁, …, х_nА также истинна в любой интерпретации α, а потому формула`В ложна в любой интерпретации α. Отсюда следует, что множество формул 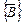невыполнимо.

Тогда по теореме о выполнимости множество 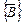противоречиво, т.е. существует формула С языка α, такая, что ├─ .

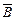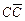Но тогда по следствию из теоремы дедукции ├─ B. Теперь, применяя n раз аксиому V₁ и правило заключения, получим ├─ A, что и доказывает теорему Гёделя.

В качестве других следствий теоремы о выполнимости докажем так называемую теорему о совместной выполнимости и локальную теорему Мальцева.

Теорема 9.36 (о совместной выполнимости). Если замкнутая формула А исчисления α истинна в любой интерпретации α, в которой истинны формулы некоторого Т замкнутых формул, то Т├─ А.

Доказательство. Из условия видно, что множество формул 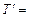Т U невыполнимо. Значит, по теореме о выполнимости множество 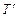противоречиво, т.е. T, 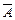├─ 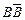для некоторой формулы В. Отсюда по следствию из теоремы дедукции Т├─ А.

Теорема Мальцева (9.37). Множество замкнутых формул S исчисления α выполнимо тогда и только тогда, когда выполнимо любое его конечное подмножество.

Доказательство. Выполнимость конечных подмножеств выполнимого множества формул очевидна. Докажем обратное утверждение. Допустим, что выполнимо любое конечное подмножество формул множества S, а само S невыполнимо. Тогда по теореме о выполнимости оно противоречиво, т.е. найдется такая формула А, что S├─ .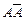

Но тогда 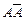выводима лишь из конечного подмножества S₁ Ì S формул, участвующих в выводе формулы 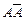из S. Следовательно, нашлось противоречивое конечное множество формул из S. Если бы S было выполнимым, то по теореме 9.28 нашлась бы интерпретация α, в которой была бы истинной формула 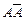, что невозможно. Полученное противоречие и доказывает теорему.

Л е к ц и я 10