Алгебраические системы. Булевы алгебры
Определение 7.1. Множество M с заданными на нём операциями и отношениями называется алгебраической системой. При этом M называется основным множеством системы, а множество символов, используемых для обозначения определённых на M операций и отношений называется сигнатурой алгебраической системы.
Алгебраическую систему с основным множеством M и сигнатурой 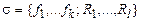 , состоящий из символов операций fi арностей ni и отношений Rj арностей mj, обозначают в виде M(
, состоящий из символов операций fi арностей ni и отношений Rj арностей mj, обозначают в виде M( 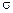 ), или подробнее M(
), или подробнее M( 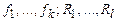 ). При этом набор натуральных чисел <n1, …, nk; m1, …, ml> называется типом алгебраической системы M(
). При этом набор натуральных чисел <n1, …, nk; m1, …, ml> называется типом алгебраической системы M( 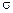 ). Если на алгебраической системе определены только операции, то она называется алгеброй. Если на алгебраической системе только отношения, то она называется моделью.
). Если на алгебраической системе определены только операции, то она называется алгеброй. Если на алгебраической системе только отношения, то она называется моделью.
Пример 7.2. N(+, *; =, <) — алгебраическая система.
Пример 7.3. N(+, *) — алгебра.
Пример 7.4. N(+, <) — модель.
Пример 7.5. Алгебрами являются полугруппы, группы, кольца, поля и т.д.
В математической логике особую роль играют так называемые булевы алгебры.
Определение 7.6. Булевой алгеброй называется множество B с двумя бинарными операциями «  », «
», « 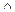 », и одной унарной операцией «¢» и двумя нуль-арными операциями (т.е. выделенными элементами) 0, 1, удовлетворяющими условиям (при любых
», и одной унарной операцией «¢» и двумя нуль-арными операциями (т.е. выделенными элементами) 0, 1, удовлетворяющими условиям (при любых 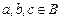 ):
):
1. 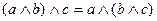 ,
,
2. 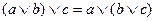 ,
,
3. 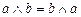 ,
,
4. 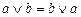 ,
,
5. 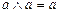 ,
,
6. 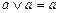 ,
,
7.  ,
,
8.  ,
,
9. 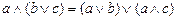 ,
,
10. 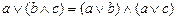 ,
,
11. 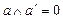 ,
,
12. 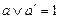 .
.
Несложно показать, что из условий 1-12 следуют равенства:
 ,
, 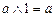 ,
,  ,
, 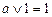 ,
,
 ,
, 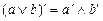 .
.
Например, выведем из условий 1-12 равенство  :
:
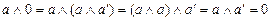 .
.
Элементы 0 и 1 булевой алгебры B называют её нулём и единицей. Иногда их обозначают в виде 0B и 1B.
Пример 7.7. Пусть 2M — обозначение множества всех подмножеств множества M, 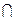 — бинарная операция пересечения множеств,
— бинарная операция пересечения множеств, 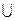 — бинарная операция объединения множеств. Для A
— бинарная операция объединения множеств. Для A 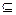 M обозначим A¢ = M\A, A¢ — дополнение множества A. «¢» — унарная операция,
M обозначим A¢ = M\A, A¢ — дополнение множества A. «¢» — унарная операция,  и M – нуль-арные операции, играющие роль 0 и 1. Тогда 2M(
и M – нуль-арные операции, играющие роль 0 и 1. Тогда 2M( 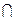 ,
, 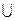 ,
,  , M) — булева алгебра.
, M) — булева алгебра.
Пример 7.8. Пусть M — множество всех положительных делителей числа m, равного произведению некоторых различных простых чисел. Определим операции «  », «
», « 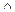 » и «¢» следующим образом: для любых
» и «¢» следующим образом: для любых 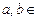 M положим
M положим 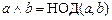 ,
, 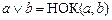 ,
, 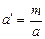 . Число 1 M играет роль нуль-арной операции 0. Число m M играет роль нуль-арной операции 1. Тогда M(
. Число 1 M играет роль нуль-арной операции 0. Число m M играет роль нуль-арной операции 1. Тогда M( 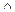 ,
,  , ¢, 1, m) — булева алгебра.
, ¢, 1, m) — булева алгебра.
Определение 7.9. Пусть 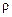 — бинарное отношение на на M. Бинарное отношение
— бинарное отношение на на M. Бинарное отношение 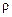 на множестве M называется отношением частичного порядка (или просто отношением порядка), если оно рефлексивно, транзитивно, антисимметрично. Отношение частичного порядка r на М называется отношением линейного порядка, если для любых x, x¢ Î M либо xr x¢, либо x¢r x. Отношение порядка обозначается через «
на множестве M называется отношением частичного порядка (или просто отношением порядка), если оно рефлексивно, транзитивно, антисимметрично. Отношение частичного порядка r на М называется отношением линейного порядка, если для любых x, x¢ Î M либо xr x¢, либо x¢r x. Отношение порядка обозначается через « 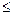 ». Если
». Если 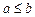 и
и 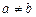 , то пишут
, то пишут  .
.
Множество M с заданным на нём отношением частичного или линейного порядка « 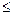 » называется, соответственно, частично или линейно упорядоченным множеством.
» называется, соответственно, частично или линейно упорядоченным множеством.
В некоторых случаях при изучении частично упорядоченных множеств используются их геометрические изображения — диаграммы. При построении диаграмм частично упорядоченного множества M( 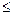 ) различные элементы из M отождествляются с различными точками плоскости так, что:
) различные элементы из M отождествляются с различными точками плоскости так, что:
точка 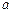 лежит левее (или ниже) точки
лежит левее (или ниже) точки 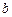 , если
, если 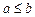 ;
;
точка 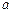 соединяется отрезком с отличной от неё точкой
соединяется отрезком с отличной от неё точкой 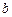 , если
, если 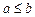 и не существует точки
и не существует точки 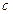 , отличной от a, b, удовлетворяющей условию
, отличной от a, b, удовлетворяющей условию 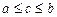 (в этом случае говорят, что b непосредственно следует за a или a непосредственно предшествует b).
(в этом случае говорят, что b непосредственно следует за a или a непосредственно предшествует b).
Пример 7.10. M = 2{1, 2, 3}.
Положим для любых A, B 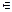 M,
M,  . Тогда диаграмма для M(
. Тогда диаграмма для M( 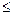 ) представляется рис.7.1.
) представляется рис.7.1.
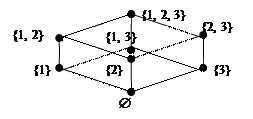 |
Рис.7.1
Пример 7.11. M = { 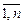 }.
}.
Положим a 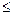 b «натуральное число a»
b «натуральное число a» 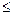 «натурального числа b». Тогда диаграмма для M(
«натурального числа b». Тогда диаграмма для M(  ) имеет вид, показанный на рис.7.2.
) имеет вид, показанный на рис.7.2.
| | | |
|
| ||||||||||
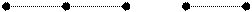 |
Рис.7.2
Пример 7.12. M = {1, 2, 3, 4, 5, 6}.
Положим a 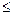 b
b 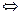 a | b для любых a, b
a | b для любых a, b 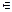 M. Тогда диаграмма для M(
M. Тогда диаграмма для M( 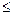 ) имеет вид (рис.7.3).
) имеет вид (рис.7.3).
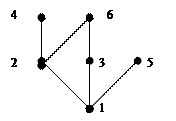 |
Рис.7.3
Интересно отметить связь булевых алгебр с частично упорядоченными множествами.
Пусть B — произвольная булева алгебра. Для произвольных элементов a, b 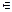 B положим a
B положим a 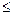 b
b 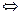 a
a  b = b.
b = b.
Из условий 6.4.2 следует, соответственно, что так определённое отношение « 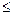 » на B рефлексивно, антисимметрично и транзитивно. В итоге имеем частично упорядоченное множество B(
» на B рефлексивно, антисимметрично и транзитивно. В итоге имеем частично упорядоченное множество B( 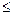 ). Диаграмма для B(
). Диаграмма для B( 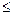 ) называется диаграммой булевой алгебры B. Таким образом на рис.7.1 изображена диаграмма булевой алгебры всех надмножеств множества {1, 2, 3}.
) называется диаграммой булевой алгебры B. Таким образом на рис.7.1 изображена диаграмма булевой алгебры всех надмножеств множества {1, 2, 3}.
Дата добавления: 2022-05-27; просмотров: 228;











