Интегральные операции векторного анализа.

В векторном анализе различают интеграл по переменной t (интеграл по параметру) и более сложные линейные, поверхностные и объемные интегралы от скалярных и векторных функций.

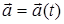
1. Интеграл от вектора по параметру. Рассмотрим вектор , что эквивалентно развернутой записи a_x = a_x(t), a_y = a_y(t), a_z = a_z(t). Пусть t₁ и t₂ – два произвольных значения переменной t. По определению имеем:

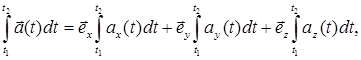
т.е. интегрирование фактически производится по каждой проекции векторной функции отдельно.

2.Линейный интеграл и циркуляция вектора. Пусть в каждой точке M области D двумерного или трехмерного пространства задано векторное поле 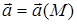, МÎD. Пусть в области D определена дуга АВ (некоторая пространственная, в частном случае – плоская кривая с выбранным направлением обхода от точки А к точке В). Будем считать, что дуга АВ может быть представлена конечной совокупностью направленных отрезков 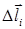. Составим скалярное произведение вида 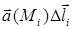, где 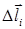ÎАВ и произведем суммирование указанных произведений. Линейным интегралом от векторного поля 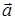по дуге АВ назовем следующий предел:

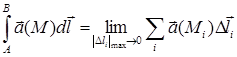
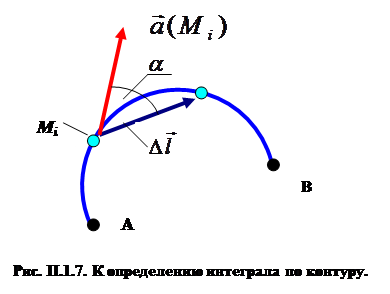
Из рисунка П.1.7 легко видеть, что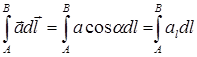

При практическом вычислении линейного интеграла важно помнить, что 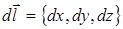, при этом действительно независимой величиной является одна из проекций dx, dy или dz, две другие связаны с выбранной величиной и определяются направлением отрезка 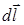в пространстве.

Линейный интеграл от векторного поля 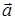, по замкнутой пространственной или плоской кривой L: 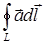называют циркуляцией вектора 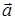по контуру L, (при записи циркуляции у значка интеграла кружок символизирует замкнутый контур). В общем случае и линейный интеграл и циркуляция зависят от конкретной формы кривой. Заметим, что при смене направления обхода дуги АВ или замкнутой кривой L, линейный интеграл и циркуляция вектора меняют знак на противоположный.

3.Интеграл от скалярной величины по поверхности.Пусть в некоторой области D поверхности S задано скалярное поле j(М), где МÎD. Допустим, что область D является объединением конечного числа элементов поверхности DS_i без общих точек, исключая граничные точки элементов. Составим сумму произведений вида

,

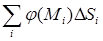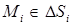
и вычислим предел этой суммы при ( DS_i )_max® 0. Интегралом от скалярной величины по поверхности D назовем указанный предел:

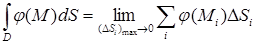
При практическом вычислении описываемого интеграла важно уметь вычислить явно выражение для площади элемента поверхности dS. Если поверхность S задана уравнением вида F(x,y,z)=0 ( действительно, это неявное задание, например, аппликаты z через абсциссу x и ординату y ), то для произвольной точки поверхности M(x,y,z) можно определить нормаль к поверхности 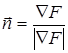и вычислить модуль направляющего косинуса нормали 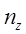, например. Элемент поверхности dS при этом можно вычислить по формуле

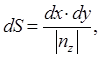
если величина 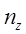не обращается в нуль. Если это не так, аналогичные вычисления можно проделать с другой проекцией вектора нормали.

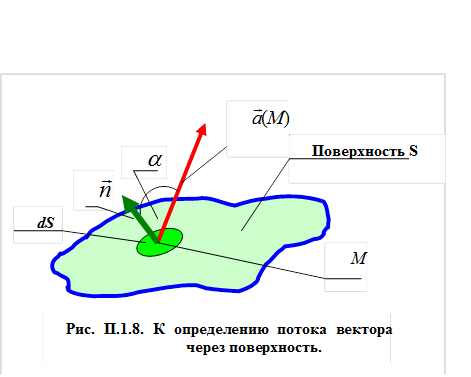
4.Поток вектора через поверхность. Рассмотрим произвольную поверхность S. Выделим на рассматриваемой поверхности элемент поверхности dS в окрестности точки M(x,y,z) и вычислим единичную нормаль 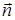к этому элементу. Нормаль 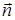однозначно определяет ориентацию в пространстве элемента dS. Произведение 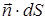часто обозначают 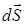, считая, что тем самым построен вектор элемента поверхности.

Если в точке М задана векторная величина 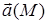, то можно ввести понятие элементарного потока вектора 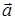через площадку 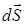как скалярное произведение рассматриваемых векторов (рис. П.1.8):

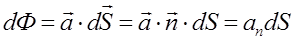
Вторая форма записи величины dФ удобна тем, что перед обычным дифференциалом площади поверхности стоит скалярная величина, интегрирование которой подробно рассмотрено в предыдущем разделе.

Потоком вектора 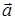через поверхность Sназывают интеграл

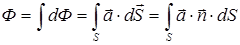
Потоком вектора 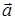через замкнутую поверхность S называют интеграл

,

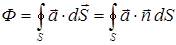где кружок у знака интеграла отмечает это особое свойство области интегрирования. Поток вектора через поверхность является скалярной величиной.

Происхождение понятия «поток вектора» связано с гидромеханикой. Если векторное поле – поле скорости жидкости 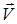, то поток вектора 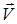через поверхность S, т. е. величина

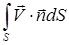
численно равна объемному расходу жидкости через эту поверхность (объёму жидкости, протекающий через поверхность S за единицу времени), если при этом жидкость несжимаема (r=const, где r - объемная плотность жидкости), то объемный расход пропорционален массовому расходу жидкости ( массе жидкости, протекающей через поверхность S за единицу времени). Если поверхность S является замкнутой, то массовый расход жидкости

,

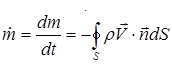где 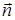– внешняя нормаль к элементу поверхности dS, либо равен нулю (все, что втекает, то и вытекает – закон сохранения массы), либо не равен нулю (внутри поверхности S имеются «источники» или «стоки» массы). Из изложенного следует, что поток вектора через замкнутую поверхность является количественной мерой суммарной мощности источников описываемого векторного поля в рассматриваемой области.

Графическая иллюстрация потока вектора через поверхность S возможна с привлечением понятия «проводимые векторные линии», описанного выше. Если для заданного векторного поля поверхность S обладает тем свойством, что каждый ее бесконечно малый элемент перпендикулярен векторной линии в точке, через которую эта линия проходит, то поток вектора можно считать (в соответствующем масштабе) равным числу проводимых векторных линий, пронизывающих поверхность S: Ф=N. На рис. П.1.9 показаны «проводимые» силовые линии, пронизывающие две поверхности, поток векторного поля через которые сохраняет свою величину.

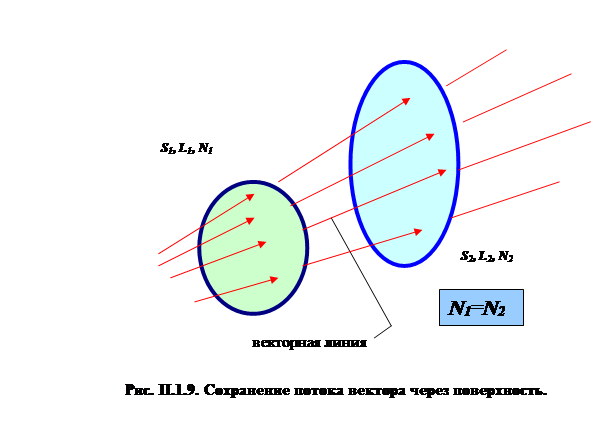
Для произвольной ориентации элемента dS относительно векторной линии графическое представление затруднено, однако, для замкнутых поверхностей имеет место следующая качественная картина. Допустим, что рассматривается некоторое векторное поле и имеется графическое изображение проводимых векторных линий в какой-то области пространства. Построим некоторую замкнутую поверхность S. Если поток векторной величины через поверхность S равен нулю, то число проводимых векторных линий, выходящих из поверхности S наружу равно числу проводимых векторных линий, входящих в S. Если же внутри поверхности S имеются «источники» (или «стоки») векторного поля, то число проводимых линий, входящих в S, не будет равно числу проводимых векторных линий, выходящих из S. Заметим, что в настоящем разделе употребляется термин «проводимая векторная линия», говорить о числе векторных линий бессмысленно, их число бесконечно практически для любой конечной поверхности, так как даже через любую малую поверхность можно провести бесконечно много линий, для каждой из которых направление вектора является касательной в рассматриваемой области. Однако, если суммарная мощность источника поля равна суммарной мощности стоков внутри замкнутой поверхности S, то соотношение

N₁=N₂,

где N₁ – число входящих, N₂ – число выходящих проводимых линий, выполняется строго.

5.Интеграл от скалярной функции по объёму определяется известным из курса математического анализа образом.

6.Интеграл от векторной функции по объёму или по поверхностивычисляется покоординатно в соответствии с представлением векторной функции через базис пространства. Такой интеграл представляет собой векторную величину.