Дифференциальные операции векторного анализа

Из курса математического анализа известно понятие производной от функции у(х) по переменному х:

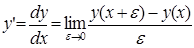.(1)

Значение производной у′(х) характеризует увеличение функции у(х) при изменении независимого переменного х, отнесённое к единичному интервалу изменения переменного х, т.е. интенсивность возрастания функции у(х). Понятно, почему математическая структура (1) находит широчайшее применение в физике.

Ниже нам понадобится понятие “частной производной” функции нескольких независимых переменных по выбранному независимому переменному, например, по времени t:

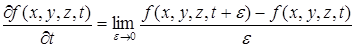. (2)

Легко видеть, что частная производная (2) вычисляется аналогично производной (1) в предположении, что все остальные независимые переменные, кроме рассматриваемого, остаются неизменными.

В соответствии с правилом (2) можно рассматривать частные производные более высокого порядка, в том числе и так называемые “перекрёстные” или “смешанные” производные (например, ).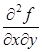

Производные по правилу (2)можно вычислять от скалярных величин или от проекций векторной величины на координатные оси, например, 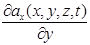и т.п.

Ниже нас, в основном, будут интересовать такие дифференциальные операции, результатом которых являются скалярные или векторные величины, т.е. объекты с определёнными трансформационными свойствами. Последнее важно как для составления уравнений, описывающих физические поля, так и для выяснения физической природы и математических свойств таких уравнений.

Рассмотрим важнейшие дифференциальные операции векторного анализа.

1. Частная производная по времени от скалярной величины 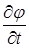вычисляется по правилу (2) и является, так же как величина 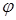, скалярной величиной в обычном трёхмерном пространстве.

2.Частная производная по времени от векторной величины 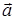представляет собой векторную величину 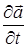, вычисляемую в декартовой системе координат по правилу:

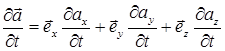(3)

Легко заметить, что правило (3) сводится фактически к вычислению частных производных по времени по правилу (2) от проекций вектора 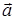на координатные направления (орты не изменяют своей ориентации в пространстве).

3. Производная по координате, например, х от векторной величины 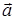вычисляются аналогично правилу (3):

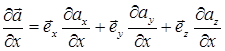
4.Производной вектора 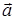по вектору 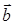называется вектор

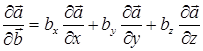, (4)

его проекции на оси декартовой системы x, y, z соответственно равны:

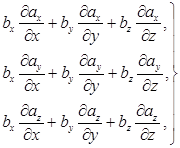. (4′)

Легко видеть, что производная 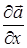является частным случаем 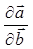при условии 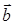={1,0,0}, т.е., если вектор 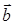является ортом направления x.

5. Наиболее важные свойства скалярных и векторных полей описываются следующими функциями:

– градиент – векторная функция, аргументом которой является скалярная функция точки пространства;

– дивергенция (расходимость) – скалярная функция, аргументом которой является векторная функция точки пространства;

– ротор (вихрь) – векторная функция, аргументом которой является векторная функция точки пространства;

– лапласиан – скалярная (векторная) функция, аргументом которой является скалярная (векторная) функции точки пространства.

Все перечисленные функции являются результатами соответствующих дифференциальных операций по пространственным переменным и отражают локальные свойства скалярных и векторных полей.

Ниже приведем определения указанных функций в декартовых системах координат ( в произвольных системах координат аналитические выражения для рассматриваемых функций будут другими!).

6. Градиент. Градиентом скалярной функции 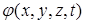называется вектор

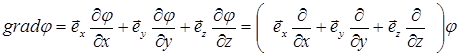. (5)

Если рассмотреть поверхность уровня скалярного поля j, проходящую через точку М (в определённый момент времени t), и близкую к ней точку М′, так что вектор 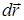с проекциями {dx,dy,dz} на координатные направления x,y,z лежит на этой поверхности, то, очевидно (правило полного дифференциала):

.

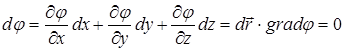Из полученного соотношения следует, что вектор gradj ортогонален вектору 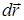, а поскольку 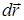можно выбрать произвольно, то говорят, что вектор gradj ортогонален поверхности уровня j в окрестности точки М. (рис. П.1.6). Последнее позволяет вычислить орт нормали к поверхности уровня j=const в точке М:

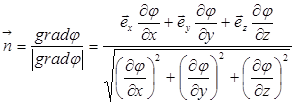. (6)

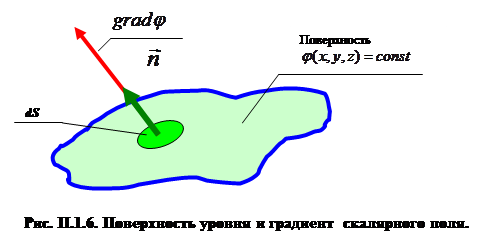
Из всего сказанного выше следует, что направление вектора gradj совпадает с направлением наибольшего возрастания функции j на единицу длины, а модуль вектора gradj равен абсолютному значению указанной величины.

С понятием gradj тесно связано понятие “нормальной производной”:

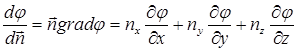(7)

Выражение (7) описывает приращение величины j в направлении орта 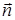в пересчёте на единицу длины.

Заметим, что для производной скалярного поля по заданному ортом 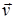произвольному направлению имеет место аналогичное соотношение:

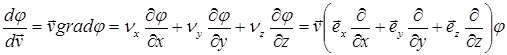. (8)

7. Дивергенция (расходимость). Пусть известна векторная функция 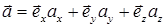, где 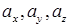– функции точки М(x,y,z) и времени t. Дивергенцией вектора 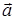называют скалярную величину

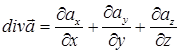. (9)

Заметим, что правая часть соотношения (9) может быть переписана в виде:

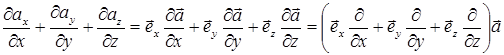. (10)

8. Ротор (вихрь). Ротор вектора 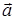– это векторная величина, определяемая по правилу:

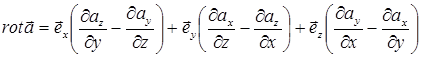. (11)

Правую часть определения (11) можно записать в следующей форме:

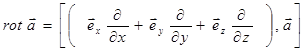. (12)

Запомнить соотношение (11) трудно, а правильно записать компоненты вектора 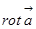можно, если воспользоваться следующей формулой определения ротора:

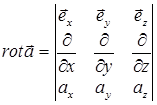, (13)

где дифференциальные операторы 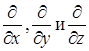при раскрытии определителя по первой строке должны быть записаны перед величинами 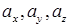, а не после них.

Физический смысл и геометрическую интерпретацию определений (9) и (11) обсудим ниже.

9. Лапласиан. Лапласианом скалярной функции 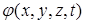называют скалярную величину:

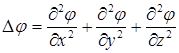. (13)

Лапласианом векторной функции 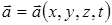называют векторную величину:

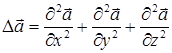. (14)

При этом, очевидно, в проекции на выделенное координатное направление имеем:

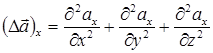и т.д.

Заметим, что определение (13) формально можно переписать в форме:

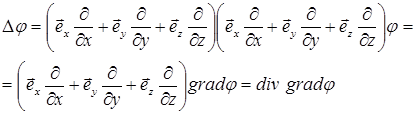(15)

Операция вычисления «лапласиана» является одной из самых распространенных по использованию дифференциальных операций второго порядка (выше рассматривались операции первого порядка).

Физический смысл выражений (13) и (14) во многом определяется смыслом величин j или соответственно, но, если рассматривать функцию , то 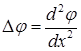, что с точностью до бесконечно малых второго порядка описывает локальную кривизну функции 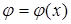. В пространстве трёх измерений 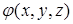при двух фиксированных из трёх аргументов представляет собой функцию одного переменного, значит, геометрический смысл каждого слагаемого в лапласиане можно считать установленным: лапласиан от скалярного поля – это сумма соответствующих кривизн сечений функции 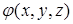координатными плоскостями.

В качестве примера можно рассмотреть поверхность мыльной плёнки, натянутой на криволинейный неплоский контур-проволоку. “Кривая” поверхность плёнки описывается при этом уравнением 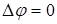с граничным условием 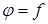на контуре, при этом алгебраическая сумма описанных выше кривизн равна нулю в каждой точке поверхности плёнки. Физически это ясно: искривление пленки связано с воздействием внутренних (натяжение пленки) и внешних сил, действующих на пленку, эффективная кривизна пленки равна нулю, если внешние силы отсутствуют.