Частота и период колебаний

Колебания систем с одной и с несколькими степенями свободы

Свободные колебания систем с одной степенью свободы

Частота и период колебаний

Если упругая система в результате взаи­модействия с каким-либо другим физическим телом оказывается выведенной из состояния равновесия, то после прекращения указанно­го взаимодействия система будет совершать свободные колебания.

Свободные колебания системы с одной степенью свободы рассмотрим на примере балки, жестко заделанной одним концом с точечной массой на сво­бодном конце (рис. 1). Из основного уравнения динамики (второй закон Ньютона) масса выражается как частное от деления силы веса груза Q на величину ускорения свободного падения g = 981 см/с², т. е.

m = Q/g, или Q = mg. (1)

Рис. 1

Таким образом, в технической системе единиц размерность массы выра­жается в кгс×с²/см.

Под действием груза Q точка его приложения переместится вниз на ве­личину у_СТ. На рис. 1 упругая линия балки от статической силы Q изо­бражена сплошной кривой линией.

Силу веса можно исключить из рассмотрения, так как она уравновеши­вается начальной силой реакции системы.

При свободных колебаниях балки в любой момент времени на массу m, отклонившуюся от положения статического равновесия на величину у, будет действовать восстанавливающая сила R, сила сопротивления F и сила инерции X. Рассмотрим каждую из этих сил, считая положитель­ными силы, перемещения, скорости и ускорения, направленные вниз.

Восстанавливающая сила R — это сила упругой реак­ции системы, возникающая при отклонении массы m от положения статичес­кого равновесия. Эта сила, стремящаяся вернуть массу в положение ста­тического равновесия, направлена в сторону, противоположную переме­щению, и в соответствии с принятым правилом знаков должна считаться отрицательной. Восстанавливающая сила пропорциональна величине от­клонения у точки, в которой сосредоточена масса, т. е.

R = -ry. (2)

Коэффициент пропорциональности г представляет собой реакцию балки в рассматриваемой точке при перемещении этой точки, равном единице. Эта величина, зависящая от упругих и геометрических характеристик сис­темы, может быть найдена из общего выражения для перемещения, вызван­ного силой г и приравненного единице, т. е.

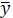= δ₁₁ r = 1, или r = 1/ δ₁₁,

где δ₁₁ — перемещение рассматриваемой точки, вызванное единичной силой.

Так, например, для рассматриваемой балки, жесткость которой равна EJ, при действии силы Q = 1 имеем:

δ₁₁ = 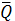l³/(3EI) = l³/(3EI) и r = 3EI/ l³.

Сила сопротивления F возникает от внутреннего трения в не вполне упругом материале, от трения в соединениях элементов кон­струкции и в опорных устройствах и из-за сопротивления внешней среды, т. е. воздуха или воды. При всех этих неупругих сопротивлениях происхо­дит рассеяние энергии.

Для упрощения математической стороны задачи обычно принимают, что сила сопротивления F пропорциональна скорости колебаний v = у^′, что она приложена к массе и направлена в сторону, противоположную ее движению. Последнее учитывается знаком «минус»:

F = – k 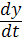= – ky. (3)

Здесь k — коэффициент пропорциональности, физический смысл которого мы установим ниже; t — время.

Сила инерции X в соответствии с принципом Даламбера равна произведению массы m на ее ускорение, т. е. на вторую производную пути или перемещения у по времени t. Эта сила направлена в сторону, противо­положную ускорению, и считается отрицательной:

Х = — m 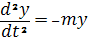^′′ (4)

Уравнение динамического равновесия всех сил, действующих на массу,

SY=X + F + R = 0.

Сила Q в это уравнение не входит, так как ее действие уже учтено тем, что перемещения отсчитываются не от нуля, а от уровня статического рав­новесия.