Яблонский А.А. Курс теоретической механики. Ч. 1 и 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания
Контрольные задания для СРС – показать применение правила Жуковского для определения ускорения Кориолиса на примере движущихся точек по поверхности Земли по меридианам и параллелям в разных направлениях.
Лекция 9. Динамика материальной точки
Цель лекции – изложить основные законы динамики, рассмотреть две основные задачи динамики точки
План лекции
1. Предмет динамики. Аксиомы динамики
2. Дифференциальные уравнения движения материальной точки. Две основные задачи динамики точки.
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Динамика является основным и наиболее общим разделом теоретической механики. В динамике изучают зависимость между движением материальных объектов и действующими на них силами.
Соотношения между основными понятиями динамики определяются аксиомами или основными законами движения, данными Ньютоном.
1 аксиома (1 закон Ньютона). Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
2 аксиома (2 закон Ньютона). Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе, совпадает с ней по направлению и обратно пропорционально массе точки.
Математически этот закон можно записать в виде
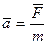 , (1)
, (1)
где 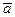 - ускорение точки,
- ускорение точки, 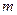 - характеризует инертные свойства точки и называется массой.
- характеризует инертные свойства точки и называется массой.
3 аксиома (3 закон Ньютона).Всякому действию всегда есть равное и противоположно ему направленное противодействие, иначе – силы взаимодействия двух тел равны между собой и направлены в противоположные стороны.
4 аксиома. Если на материальную точку действует система сил 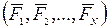 , то действие каждой из сил не зависит от действия остальных и каждая из сил сообщает точке такое ускорение, какое она ей сообщила бы, если бы действовала одна, а под действием системы сил точка получает ускорение
, то действие каждой из сил не зависит от действия остальных и каждая из сил сообщает точке такое ускорение, какое она ей сообщила бы, если бы действовала одна, а под действием системы сил точка получает ускорение
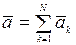 ,
,
где 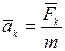 . В этом заключается принцип независимости действия сил.
. В этом заключается принцип независимости действия сил.
Так как ускорение точки связано с ее радиус-вектором 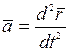 , а сила в рамках классической механики может быть функцией времени, положения и скорости точки, из уравнения (1) получаем векторное дифференциальное уравнение движения точки:
, а сила в рамках классической механики может быть функцией времени, положения и скорости точки, из уравнения (1) получаем векторное дифференциальное уравнение движения точки:
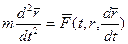 . (2)
. (2)
В проекциях на декартовы оси координат (базис 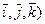 дифференциальные уравнения движения точки имеют вид:
дифференциальные уравнения движения точки имеют вид:
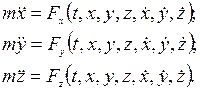 (3)
(3)
Здесь 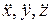 - проекции ускорения точки на координатные оси,
- проекции ускорения точки на координатные оси, 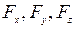 - проекции равнодействующей сил, действующих на точку.
- проекции равнодействующей сил, действующих на точку.
На основе дифференциальных уравнений движения материальной точки решают две основные задачи динамики точки:1) по движению определить силы, производящие данное движение. Эту задачу называют первой (прямой) задачей динамики точки, 2) даны силы, действующие на материальную точку; требуется определить движение этой точки под действием данных сил. Эту задачу называют второй (обратной) задачей динамики точки.
ГЛОССАРИЙ
| Динамика | Динамика | Dynamics |
| Инерттiлiк | Инертность | Inertia |
| Масса | Масса | Mass |
| Материялық нүкте | Материальная точка | Particle |
| Инерциялық санақ жүйе | Инерциальная система отсчета | Inertial reference frame |
| Күш | Сила | Force |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 2104;










