Яблонский А.А. Курс теоретической механики. Ч. 1, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания
Контрольные задания для СРС - самостоятельно изучить:
1) теорему о равенстве проекций скоростей;
2) теорему о существовании и единственности мгновенный центр скоростей (МЦС), рассмотреть различные случаи определения положения МЦС, скоростей точек плоской фигуры.
Лекция 8. Сложное движение точки
Цель лекции – изложить сложное движение точки с доказательством теоремы Кориолиса.
План лекции
Теорема о сложении скоростей. Теорема о сложении ускорений (теорема Кориолиса).
Свойства ускорения Кориолиса. Правило Н.Е. Жуковского
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Механическое движение выражается в изменении с течением времени взаимных положений тел. Такое изменение можно отметить только относительно других тел. В ряде задач механики оказывается целесообразным рассмотрение движения точки одновременно в нескольких системах координат.
Движение точки, исследуемое одновременно по отношению к нескольким системам отсчета, называют сложным.
Движение точки по отношению к подвижной системе отсчета называется относительным. Кинематические характеристики этого движения называются соответственно относительной скоростью 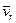 и относительным ускорением
и относительным ускорением 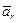 .
.
Движение, совершаемое подвижной системой отсчета и всеми неизменно связанными с нею точками пространства по отношению к неподвижной системе, называется переносным, соответственно и характеристики движения будут называться переносной скоростью 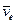 и переносным ускорением
и переносным ускорением 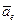 .
.
Зависимость между абсолютной 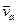 , относительной
, относительной 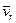 и переносной
и переносной 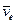 скоростями точки в сложном ее движении устанавливает теорема о сложении скоростей.
скоростями точки в сложном ее движении устанавливает теорема о сложении скоростей.
Теорема. Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей. 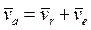 .
.
Зависимость между абсолютным, относительным и переносным ускорениями точки определяется кинематической теоремой Кориолиса:
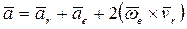 или
или 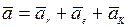 ,
,
где 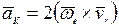 - ускорение Кориолиса.
- ускорение Кориолиса.
Таким образом, абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.
Модуль ускорения Кориолиса, если угол между векторами 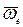 и
и 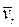 обозначить
обозначить 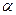 , будет равен:
, будет равен: 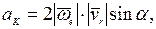
Направление вектора 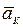 определяется правилом векторного умножения либо правилом Жуковского, согласно которому следует спроецировать вектор относительной скорости точки на плоскость, перпендикулярную оси переносного вращения и повернуть эту проекцию в этой же плоскости на 900 в сторону переносного вращения. Ускорение Кориолиса равно нулю в следующих случаях:
определяется правилом векторного умножения либо правилом Жуковского, согласно которому следует спроецировать вектор относительной скорости точки на плоскость, перпендикулярную оси переносного вращения и повернуть эту проекцию в этой же плоскости на 900 в сторону переносного вращения. Ускорение Кориолиса равно нулю в следующих случаях:
1) 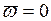 , 2)
, 2) 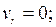 3)
3) 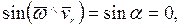 т.е.
т.е. 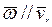 .
.
ГЛОССАРИЙ
| Нүктенiң күрделi қозғалысы | Сложное движение точки | Compound motion of particle |
| Нүктенiң абсолют қозғалысы | Абсолютное движение точки | Absolute motion of particle |
| Нүктенiң салыстырмалы қозғалысы | Относительное движение точки | Relative motion |
| Нүктенiң тасымал қозғалысы | Переносное движение точки | Bulk motion |
| Кориолис үдеуi | Ускорение Кориолиса | Carioles acceleration |
| Салыстырмалы жылдамдық (үдеу) | Относительная скорость (ускорение) | Relative velocity (acceleration) |
| Тасымал жылдамдық (үдеу ) | Переносная скорость (ускорение) | Bulk velocity (acceleration) |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 2584;










